The period of a piston in an engine, moving simple harmonically is 2 s. A body of mass 10 kg is placed on the piston. Calculate the maximum amplitude of the piston such that the mass is not thrown out from the platform.
The correct Answer is:0.993 m
To solve the problem, we need to determine the maximum amplitude of the piston such that the mass placed on it does not get thrown off. We will follow these steps:
Step 1: Understand the relationship between period and angular frequency
The period T of the piston is given as 2 seconds. The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting T=2 seconds:
ω=2π2=πrad/s
Hint: Remember that the angular frequency is related to the period by the formula ω=2πT.
Step 2: Relate acceleration to amplitude
In simple harmonic motion (SHM), the maximum acceleration a is given by:
a=ω2A
where A is the amplitude.
Hint: The maximum acceleration in SHM can be expressed in terms of angular frequency and amplitude.
Step 3: Set the condition for the mass not being thrown off
For the mass to not be thrown off the piston, the maximum acceleration must be equal to the acceleration due to gravity g:
a=g
Substituting the expression for acceleration from SHM:
ω2A=g
Hint: The condition for the mass to remain on the piston is that the maximum acceleration must not exceed gravitational acceleration.
Step 4: Solve for amplitude A
Now, substituting ω=π:
(π)2A=g
Thus, we can express A as:
A=gπ2
Hint: Rearranging the equation will allow you to isolate the amplitude.
Step 5: Substitute the value of g
Using g≈9.81m/s2:
A=9.81π2
Calculating π2≈9.87:
A≈9.819.87≈0.993m
Hint: Use the approximate value of π for calculations to find the numerical value of amplitude.
Final Answer
The maximum amplitude of the piston such that the mass is not thrown out from the platform is approximately:
A≈0.993m
The period T of the piston is given as 2 seconds. The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting T=2 seconds:
ω=2π2=πrad/s
In simple harmonic motion (SHM), the maximum acceleration a is given by:
a=ω2A
where A is the amplitude.
For the mass to not be thrown off the piston, the maximum acceleration must be equal to the acceleration due to gravity g:
a=g
Substituting the expression for acceleration from SHM:
ω2A=g
Now, substituting ω=π:
(π)2A=g
Thus, we can express A as:
A=gπ2
Using g≈9.81m/s2:
A=9.81π2
Calculating π2≈9.87:
A≈9.819.87≈0.993m
The maximum amplitude of the piston such that the mass is not thrown out from the platform is approximately:
A≈0.993m
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM TIME PERIOD OF OSCILLATION OF A S.H. OSCILLATOR)
19 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
The vertical motion of a huge piston in a machine is approximately SHM with a frequency of 1Hz.A block of mass 20 kg is placed on the piston . What is the maximum amplitude of the piston's SHM for the block and the piston to remain together .
Hint : v=12π√km
Find k
For maximum displacement xmax=A
For maximum restoring force , F=−kA=−mg
∴A=mgk=mgmω2=gω2
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM. A block of 5 kg is placed on the piston. The maximum amplitude of the piston's SHM for the block and the piston to remains together is 0.99m. Find the frequency .
Hint : v=12π√km
Find k
For maximum displacement xmax=A
For maximum restoring force , F=−kA=−mg
∴k=mgA. Put the valeu of K in v=12π√km to find v .
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate change in momentum of the body.
View SolutionA body of mass 5 kg is moving with velocity 2 ms−1. Calculate its linear momentum.
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate the velocity acquired by the body
View SolutionA block rides on position that is moving vertically with simple harmonic motion. The maximum speed of the piston is 2m/s. At what amplitude of motion will the block and piston separate? (g=10m/s2)
View SolutionThe area of cross-section of the wider tube shown in fig., is 800cm2 . If a mass of 12 kg is placed on the massless piston, what is the difference in the level of water in two tubes.

View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
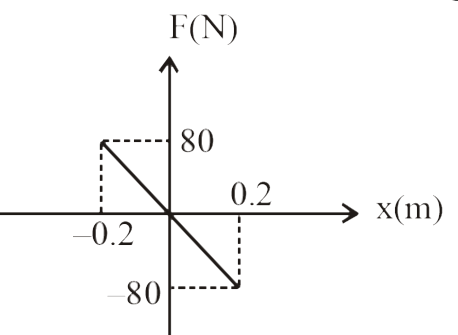
View SolutionA block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :

View Solution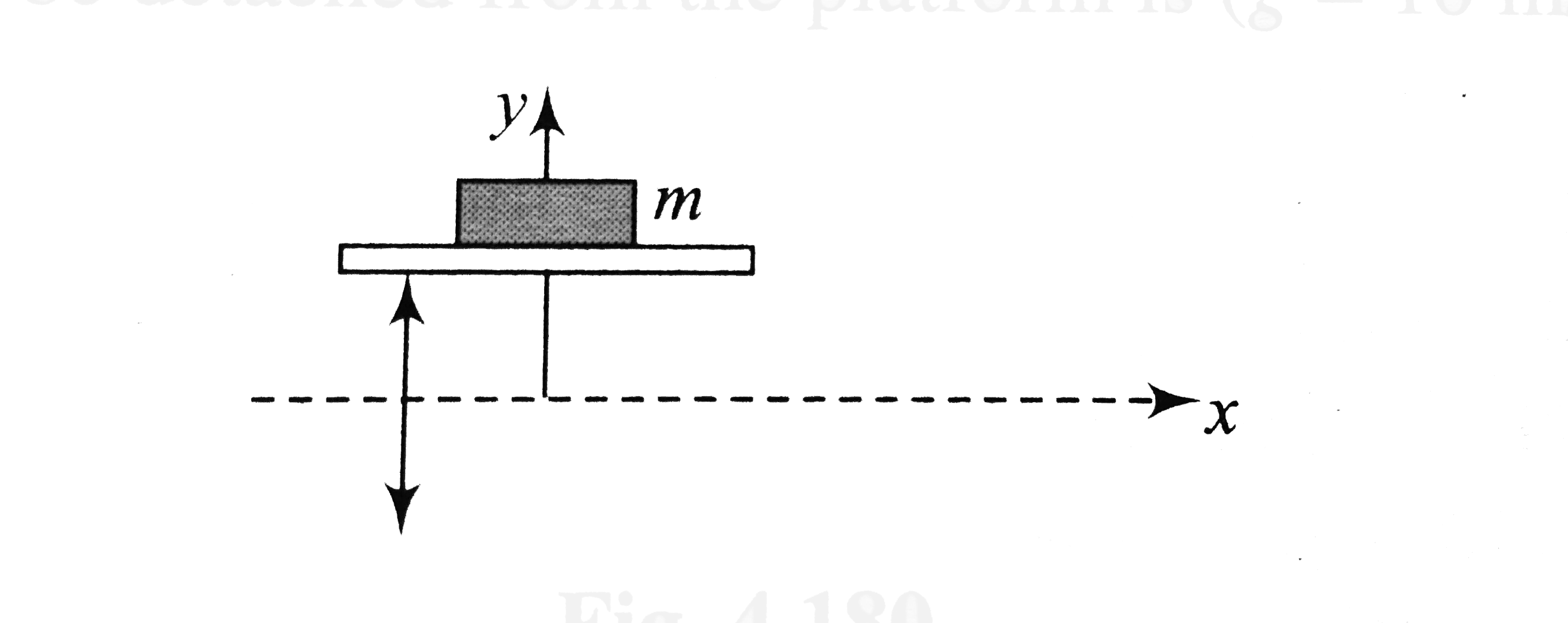
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
View Solution
