A block rides on position that is moving vertically with simple harmonic motion. The maximum speed of the piston is 2m/s. At what amplitude of motion will the block and piston separate? (g=10m/s2)
20 cm
30cm
40 cm
50 cm
The correct Answer is:C
To solve the problem, we need to determine the amplitude of motion at which the block and the piston will separate. We will use the relationship between the maximum speed of the piston, the angular frequency, and the amplitude of the simple harmonic motion.
1. Identify Given Values:
- Maximum speed of the piston, vmax=2m/s
- Acceleration due to gravity, g=10m/s2
2. Relate Maximum Speed to Angular Frequency and Amplitude:
The maximum speed vmax in simple harmonic motion is given by the formula:
vmax=ωA
where ω is the angular frequency and A is the amplitude.
3. Express Angular Frequency:
The angular frequency ω can be related to the acceleration due to gravity g and the amplitude A at the point of separation:
ω2A=g
4. Substituting for Angular Frequency:
From the first equation, we can express ω as:
ω=vmaxA
Substituting this into the second equation gives:
(vmaxA)2A=g
Simplifying this, we have:
v2maxA=g
5. Solve for Amplitude A:
Rearranging the equation to solve for A:
A=v2maxg
Now substituting the known values:
A=(2m/s)210m/s2=410=0.4m
6. Convert to Centimeters:
To express the amplitude in centimeters:
A=0.4m=40cm
Final Answer:
The amplitude of motion at which the block and piston will separate is 40 cm.
- Maximum speed of the piston, vmax=2m/s
- Acceleration due to gravity, g=10m/s2
The maximum speed vmax in simple harmonic motion is given by the formula:
vmax=ωA
where ω is the angular frequency and A is the amplitude.
The angular frequency ω can be related to the acceleration due to gravity g and the amplitude A at the point of separation:
ω2A=g
From the first equation, we can express ω as:
ω=vmaxA
Substituting this into the second equation gives:
(vmaxA)2A=g
Simplifying this, we have:
v2maxA=g
Rearranging the equation to solve for A:
A=v2maxg
Now substituting the known values:
A=(2m/s)210m/s2=410=0.4m
To express the amplitude in centimeters:
A=0.4m=40cm
The amplitude of motion at which the block and piston will separate is 40 cm.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :

View SolutionA block of mass m kg hanging from a verticla spring executes simple harmonic motion of amplitude 4 cm . If maximum speed of particle is 8m/s . Maximum acceleration of block is
View SolutionA particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm / s . The frequency of its oscillation is
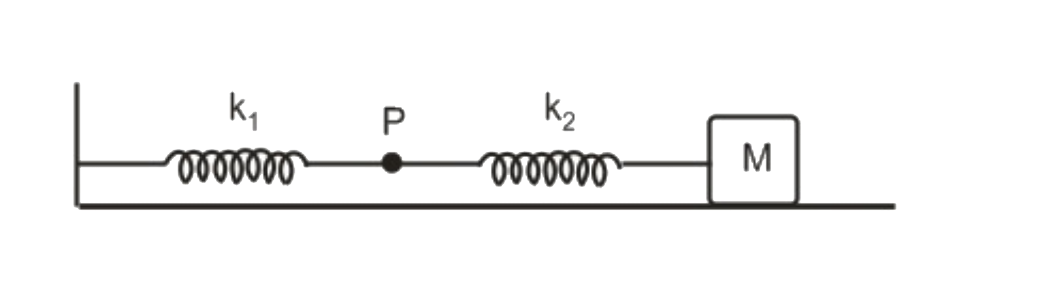
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
View SolutionA particle executing simple harmonic motion of amplitude 5cm has maximum speed of 31.4cm/s. The frequency of its oscillation is
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of 2.0s in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of 2.0s in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionConsider a simple pendulum undergoing oscillation in vertical plane following simple harmonic motion. The maximum tension in the string is double the minimum tension. What will be angular amplitude?
View SolutionThe maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View SolutionThe period of a piston in an engine, moving simple harmonically is 2 s. A body of mass 10 kg is placed on the piston. Calculate the maximum amplitude of the piston such that the mass is not thrown out from the platform.
View Solution
