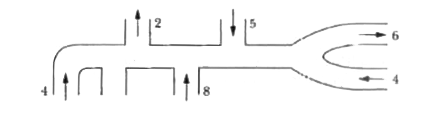
The pipe shows the volume flow rate of an ideal liquid at certain time and its direction. What is the value of Q in m3/s? (Assume steady state and equal area of cross section at each opening)

10×10−6
11×10−6
13×10−6
18×10−6
The correct Answer is:C
(σQ)inflow=(σQ)outflow
∴(4×10−6)+Q+(4×10−6)
=(8×10−6)+(2×10−6)+(5×10−6)
+(6×10−4)
∴Q=13×10−6m3/s.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
The figure shows a pipe and gives the volume flow rate (in cm3/s) and the direction of flow for all but one section . What are the volume flow rate and the direction of flow for that section ?
View SolutionTwo very large open tanks A&F both contain the same liquid. A horizontal pipe BCD, having a small constriction at C, leads out of the bottom of tank A, and a vertical pipe E containing air opens into the constriction at C and dips into the liquid in tank F. Assume stremline flow and no viscosity. If the cross section area at C is one-half that at D, and if D is at distance h1 below the level of the liquid in A, to what height h2 will liquid rise in pipe E? Express your answer in terms of h1.
[Neglect changes in atmosphere pressure with elevation. In the containers there is atmosphere above the water surface and D is also open to atmosphere.]

View Solution
Knowledge Check
The rate of flow of heat through a metal bar of area of cross-section 1 m2 when temperature gradient is 1∘C/m under steady state is called
Athermal resistanceBthermal conductivityCdiffusibilityDresistivityBlood is flowing at the rates of 200 cm3/sec in a capillary of cross-sectional area 0.5m2. The velocity of flow, (in mm/sec) is:
A0.1B0.2C0.3D0.4Certain volume of a liquid is taken in a long glass tube and its temperature is increased at a uniform rate, the rate of increase in the length of the liquid depends on
a) length of the liquid
b) area of cross section of the glass tube
c) coefficient of expansion of glassAOnly (a) is correctB(a) & (b) are correctC(b) & (c) are correctD(a),(b) & (c) are correct
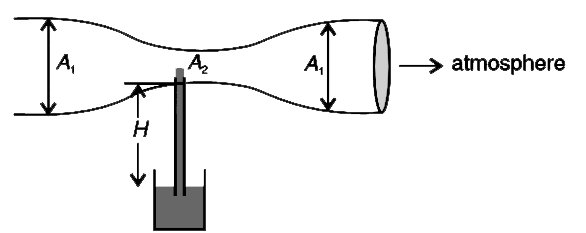
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
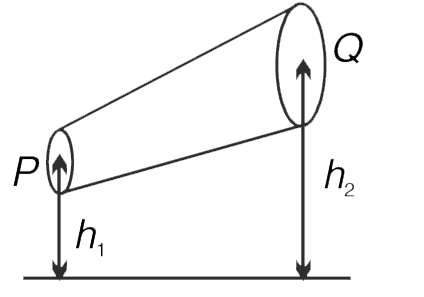
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View SolutionA Pitot tube (figure) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquid and the gas are ρ0 and ρ respectively.
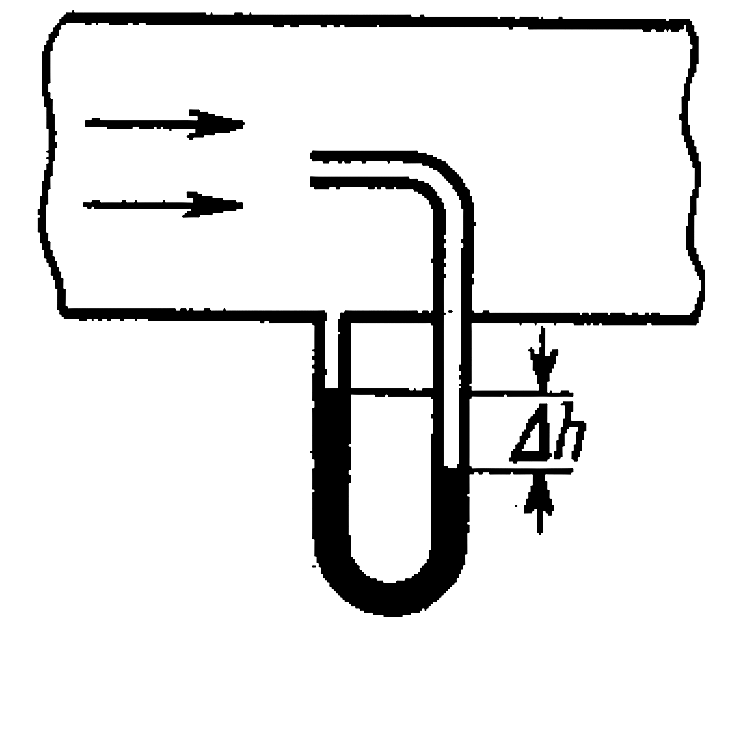
View SolutionA piot tube figure is mounted along the axis of a gas pipeline whose cross -sectional area is equal to S.

Assuming the viscosity to be negligible, find the volume of the gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquids and the gas are ρ0 and ρ respectively.
View SolutionIn the figure shown density of lower liquid is three times of density of upper liquid. The cross- sectional areas of openings shown are same. The ratio of mass flow rate from upper opening to lower opening at initial moment is:
View SolutionThe rate of volume flow of water through a canal is found to be a function of the area of cross-section of the canal and velocity of water. Show that the rate of volume flow is proportional to the velocity of flow of water.
View Solution
