A Pitot tube (figure) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquid and the gas are ρ0 and ρ respectively.
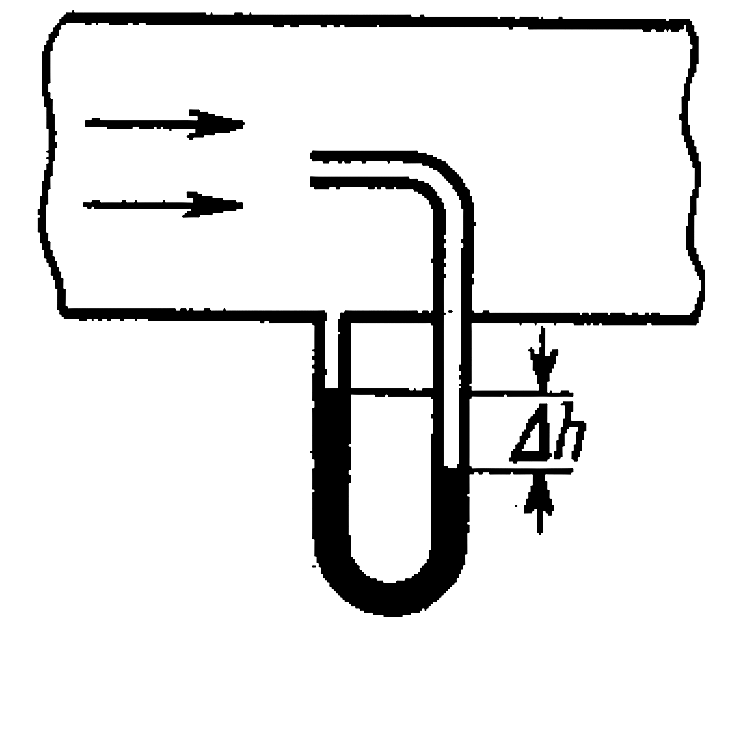
Applying Bernoulli's theorem for the point A and B,
pA=pB+12ρv2 as, vA=0
or, 12ρv2=pA−pB=Δlρ0g
So, v=√2Δhρ0gρ
Thus, rate of flow of gas, Q=Sv=S√2Δhρ0gρ
The gas flows over the tube past it at B. But at A the gas becomes stationary as the gas will move into the tube which already contains gas.
In applying Bernoulli's theorem we should remember that pρ+12v2+gz is constant along a streamline. In the present case, we are really applying Bernoulli's theorem somewhat indirectly. The streamline at A is not the streamline at B. Nevertheless the result is correct. To be convinced of this, we need only apply Bernoull's theorem to the streamline that goes through A by comparing the situation at A with that above B on the same level. In steady conditions, this agrees with the result derived because there cannot be a transverse pressure differential.

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A piot tube figure is mounted along the axis of a gas pipeline whose cross -sectional area is equal to S.

Assuming the viscosity to be negligible, find the volume of the gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquids and the gas are ρ0 and ρ respectively.View SolutionTwo manometric tubes are mounted on a horizontal pipe of varying cross-section at the section S1 and S2 (figure). Find the volume of water flowing across the pipe's section per unit time if the difference in water columns is equal to Δh.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
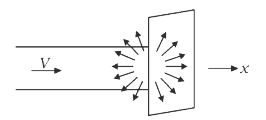 AρAV2B√2ρAV2C2ρAV2D√3ρAV2
AρAV2B√2ρAV2C2ρAV2D√3ρAV2 - Question 2 - Select One
The mass of the liquid flowing per second per unit area of cross section of the tube is proportional to Pxandvy , where P is the pressure difference and v is the velocity , then the relation between x and Y is
Ax=yBx=−yCy2=xDy=−x2 - Question 3 - Select One
A ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
A2π√BA2MV0B2π√BAMV20C2π√BAMV0D2π√B2AMV0
A tube of length l and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The fluid flow velocity depends on the distance r from the axis of the tube as v=v0(1−r2/R2). Find:
(a) the volume of the fluid flowing across the section of the tube per unit time:
(b) the kinetic energy of the fluid within the tube's volume,
(c) the friction force exerted on the tube by the fluid,
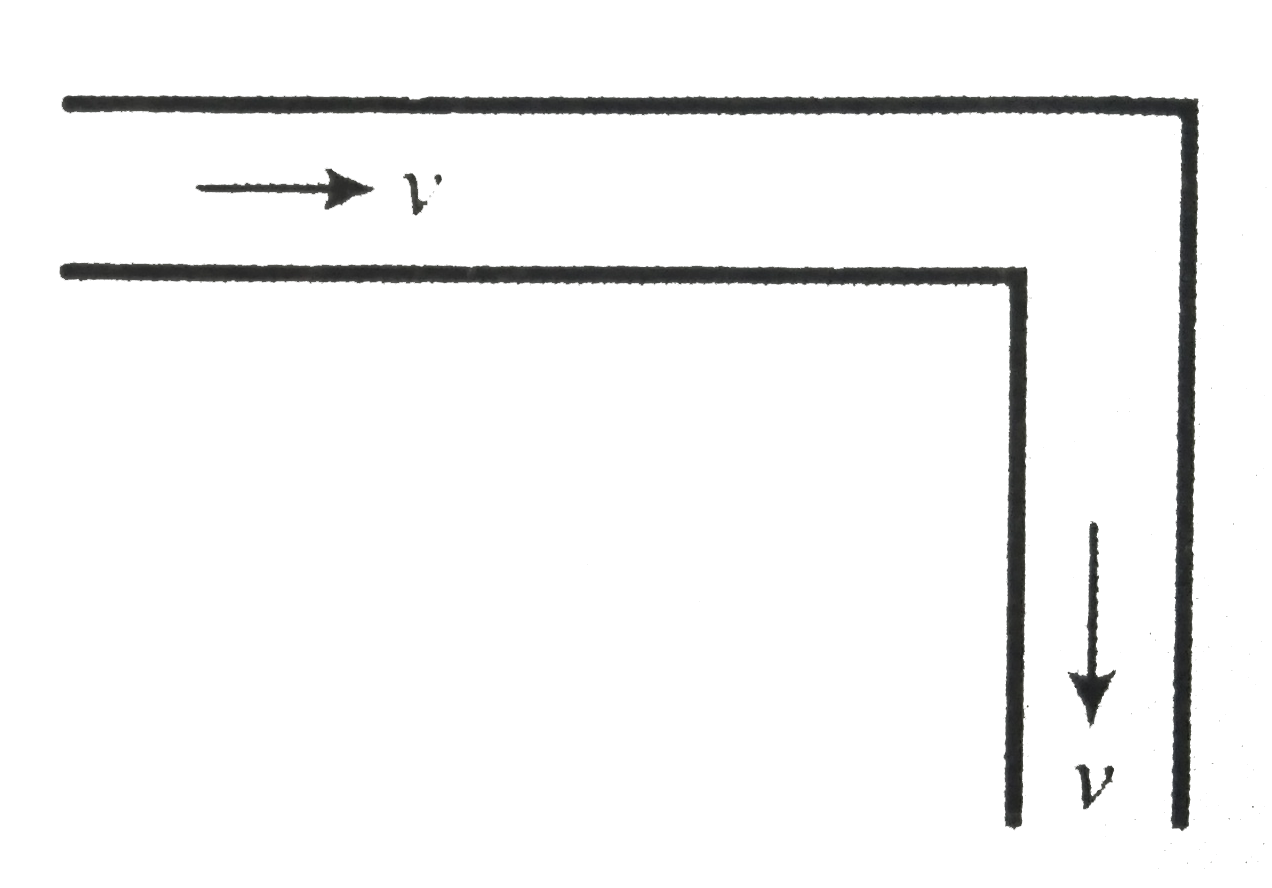
(d) the pressure difference at the ends of the tube.View SolutionA liquid of density ρ is flowing inside a pipe of cross - sectional area A. The pipe is bent in the shape of a right angle as shown. What force should be exerted on the pipe at the corner to keep it fixed in the two cases shown?
 View Solution
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
 View Solution
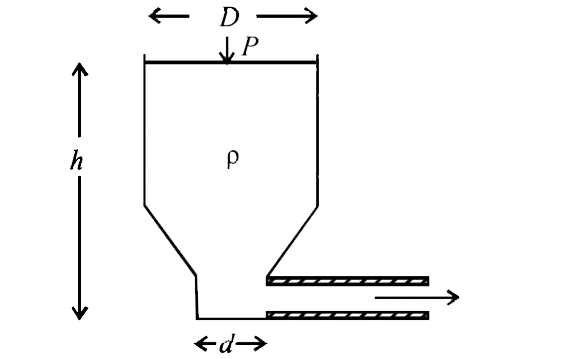
View SolutionShown in the figure is a container whose top and botoom diameters are D and d respectively. At the bottom of the container, there is a capillary tube of outer radius b and inner radius a.
The volume flow rate in the capillary is Q. If the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as ρ. Calculate the coefficient of viscosity η.
 View Solution
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
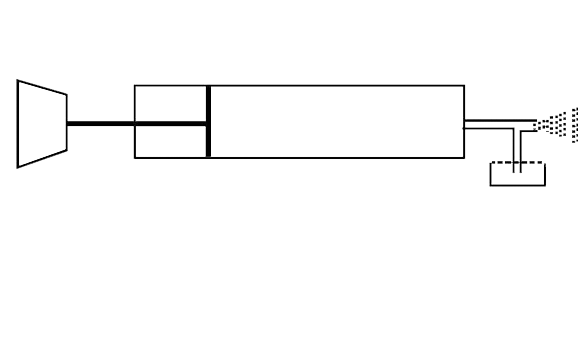
If the density of air is ρa, and that of the liquid ρl, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional toView Solution

