The plane of a circular coil is horizontal. It has 10 turns each of radius 8cm. A current of 2 A flows through it. The current appears to flow clockwise from a point above the coil. Find the magnitude and direction of magnetic field at the centre of the coil due to the current.
To find the magnitude and direction of the magnetic field at the center of a circular coil with given parameters, we can follow these steps:
Step 1: Identify the given values
- Number of turns (N) = 10
- Radius of the coil (R) = 8 cm = 0.08 m
- Current (I) = 2 A
Step 2: Use the formula for the magnetic field at the center of a circular coil
The formula for the magnetic field (B) at the center of a circular coil with N turns is given by:
B=μ0NI2R
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 3: Substitute the values into the formula
Substituting the values into the formula:
B=(4π×10−7T m/A)×10×2A2×0.08m
Step 4: Simplify the equation
First, calculate the denominator:
2R=2×0.08=0.16m
Now substituting this back into the equation:
B=(4π×10−7)×10×20.16
Step 5: Calculate the magnetic field
Calculating the numerator:
4π×10−7×10×2=8π×10−7
Now, substituting this into the equation for B:
B=8π×10−70.16
Calculating the value:
B=5π×10−6≈1.57×10−6T
Step 6: Determine the direction of the magnetic field
Since the current flows clockwise when viewed from above, the direction of the magnetic field at the center of the coil will be directed downwards (into the plane of the coil). This follows the right-hand rule, where the thumb points in the direction of the current and the fingers curl in the direction of the magnetic field.
Final Answer:
The magnitude of the magnetic field at the center of the coil is approximately 1.57×10−6T and the direction is downwards (into the plane of the coil).
---
- Number of turns (N) = 10
- Radius of the coil (R) = 8 cm = 0.08 m
- Current (I) = 2 A
The formula for the magnetic field (B) at the center of a circular coil with N turns is given by:
B=μ0NI2R
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values into the formula:
B=(4π×10−7T m/A)×10×2A2×0.08m
First, calculate the denominator:
2R=2×0.08=0.16m
Now substituting this back into the equation:
B=(4π×10−7)×10×20.16
Calculating the numerator:
4π×10−7×10×2=8π×10−7
Now, substituting this into the equation for B:
B=8π×10−70.16
Calculating the value:
B=5π×10−6≈1.57×10−6T
Since the current flows clockwise when viewed from above, the direction of the magnetic field at the center of the coil will be directed downwards (into the plane of the coil). This follows the right-hand rule, where the thumb points in the direction of the current and the fingers curl in the direction of the magnetic field.
The magnitude of the magnetic field at the center of the coil is approximately 1.57×10−6T and the direction is downwards (into the plane of the coil).
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENTBOOK - SL ARORACHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - TYPE B
6 Videos
- MAGNETIC EFFECTS OF CURRENTBOOK - SL ARORACHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - TYPE C
4 Videos
- HEATING EFFECT OF CURRENTBOOK - SL ARORACHAPTER - HEATING EFFECT OF CURRENTEXERCISE - All Questions
192 Videos
- MAGNETISMBOOK - SL ARORACHAPTER - MAGNETISMEXERCISE - Based on (i) Earth s Magnetism (ii) magnetic field of a bar magnet
60 Videos
Similar Questions
A circular coil is lying in a horizontal plane. The coil has 20 turns with each turn of radius 10 cm. For an observer above the coil, the current of 5 A appears to flow in the anticlockwise direction. What is the magnitude and direction of magnetic field at the centre of the coil?
View SolutionA wire of length L is bent around in the form of a coil having N turns of same radius . If a steady current I flows through it in a clockwise direction, find the magnitude and direction of the magnetic field produced at its centre.
View Solution
Knowledge Check
Two Concentric circular coils X and Y of radii 16cm and 10cm lie in the same vertical plane containing N−S direction X has 20 turns and carries 16A.Y has 25 truns & carries 18A.X has current in anticlockwise direction and Y has current in clockwise direction for the observer, looking at the coils facing the west. The magnitude of net magnetic field at their common centre is .
A1.6×10−5 westB1.6×10−3 eastC1.6×10−3 westD1.6×10−5 eastA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
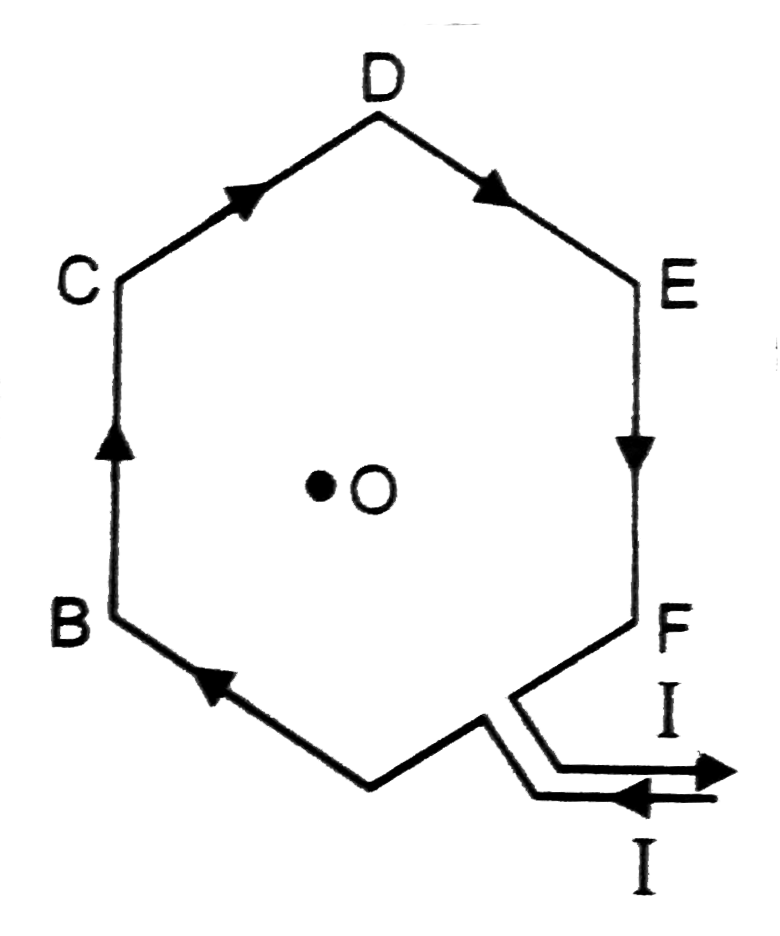 A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16A, coil Y has 25 turns and carries a current of 18 A. The sense of the current in X in antoclockwise, and clockwise in Y, for an observer looking at hte coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
View SolutionIf current through a circular coil flows in clockwise direction, then the direction of magnetic field at the centre of the circular coil is………………to the plane of the coil, directed……………. .
View SolutionA current of 5A is flowing through a 10 turn circular coil of radius 7cm. The coil lies in XY plane. What is the magnitude and direction of magnetic dipole moment associated with it?
View SolutionTwo concentric coil X and Y of radii 16cm and 10cm respectively lie in the same vertical plane containing the north-south direction. Coil X has 20 turns and carries a current of 16A, coil Y has 25 turns and carries a current of 18A. The sense of current in X is anti-clockwise and in Y, clockwise, for an observer looking at the coil facing west, Figure. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

View SolutionA current of 6A is flowing through a 20 turns circular coil of radius 5cm.The coil lies in the xy-plane. What is the magnitude and direction of the magneitc dipole moment assocaited with it?
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View Solution
