A wire of length L is bent around in the form of a coil having N turns of same radius . If a steady current I flows through it in a clockwise direction, find the magnitude and direction of the magnetic field produced at its centre.
To find the magnitude and direction of the magnetic field produced at the center of a coil formed by bending a wire of length L with N turns and carrying a steady current I, we can follow these steps:
Step 1: Determine the Radius of the Coil
The length of the wire L is equal to the circumference of the coil multiplied by the number of turns N. The circumference of a circle is given by 2πr, where r is the radius. Therefore, we can express this relationship as:
L=N⋅2πr
From this, we can solve for the radius r:
r=L2πN
Step 2: Use the Formula for Magnetic Field at the Center of the Coil
The magnetic field B at the center of a circular coil carrying a current I is given by the formula:
B=μ0NI2r
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Step 3: Substitute the Expression for Radius
Now, substitute the expression for r from Step 1 into the magnetic field formula:
B=μ0NI2(L2πN)
This simplifies to:
B=μ0NI⋅2πN2L
B=μ0πN2IL
Step 4: Determine the Direction of the Magnetic Field
To find the direction of the magnetic field, we can use the right-hand rule. Since the current flows in a clockwise direction when viewed from above, the magnetic field at the center of the coil will point downwards (into the plane of the coil).
Final Result
Thus, the magnitude of the magnetic field at the center of the coil is:
B=μ0πN2IL
And the direction of the magnetic field is downwards (into the plane of the coil).
---
The length of the wire L is equal to the circumference of the coil multiplied by the number of turns N. The circumference of a circle is given by 2πr, where r is the radius. Therefore, we can express this relationship as:
L=N⋅2πr
From this, we can solve for the radius r:
r=L2πN
The magnetic field B at the center of a circular coil carrying a current I is given by the formula:
B=μ0NI2r
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Now, substitute the expression for r from Step 1 into the magnetic field formula:
B=μ0NI2(L2πN)
This simplifies to:
B=μ0NI⋅2πN2L
B=μ0πN2IL
To find the direction of the magnetic field, we can use the right-hand rule. Since the current flows in a clockwise direction when viewed from above, the magnetic field at the center of the coil will point downwards (into the plane of the coil).
Thus, the magnitude of the magnetic field at the center of the coil is:
B=μ0πN2IL
And the direction of the magnetic field is downwards (into the plane of the coil).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
A current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
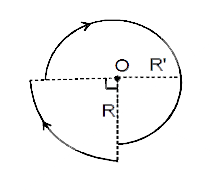 View Solution
View SolutionA circular segment of radius 20cm subtends an angle of 60∘ at its centre. Figure A current of 10A is flowing through it. Find the magnitude and direction of the magnetic field produced at the centre.
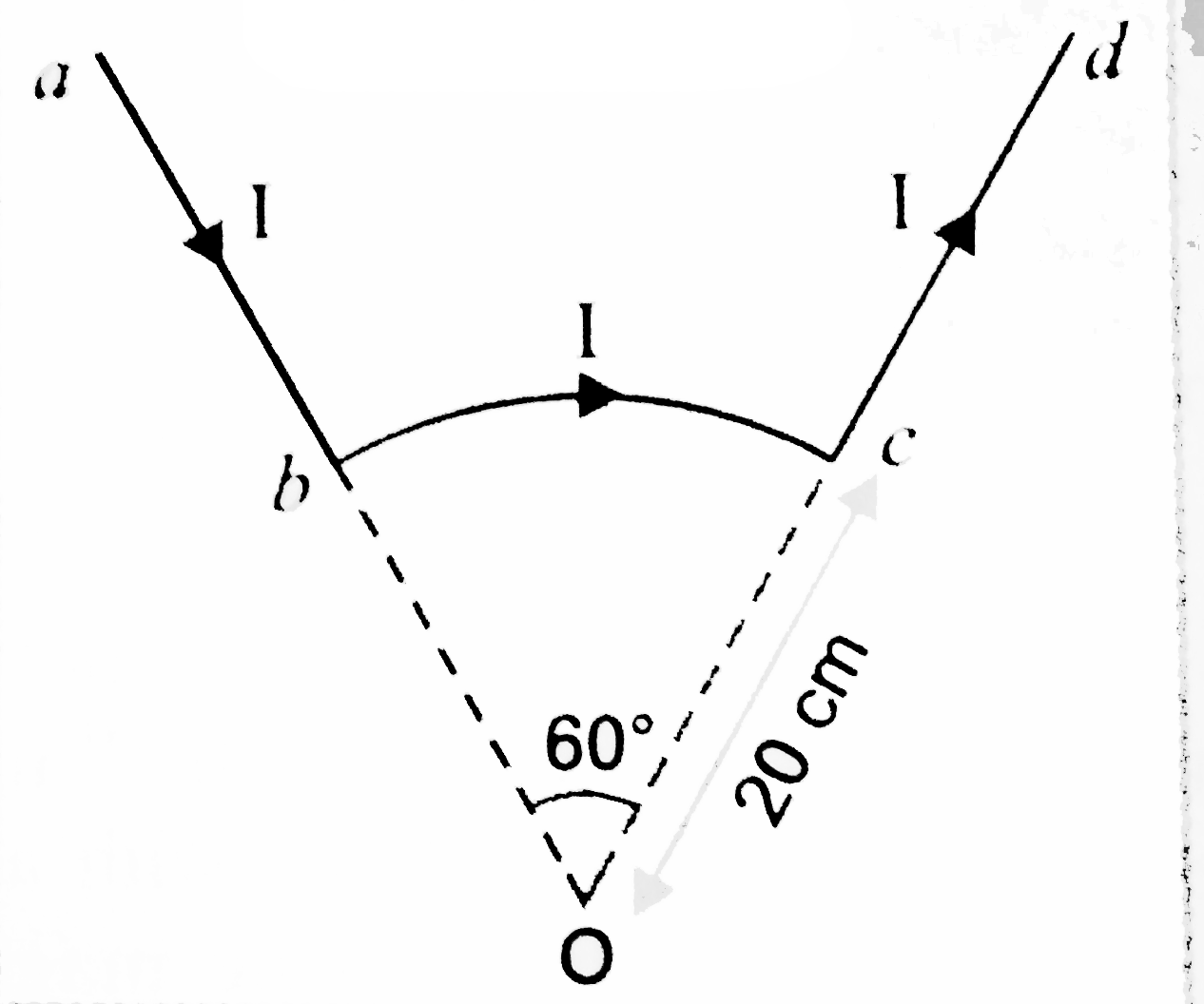 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length l is bent in the form a circular coil of some turns. A current I flows through the coil. The coil is placed in a uniform magnetic field B. The maximum torqur on the coil can be
AiBl24πBiBl2πCiBl22πD2iBl2π - Question 2 - Select One
A conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
A27μ0I4πLB27μ0I2πLC27μ0I5πLD27μ0I7πL
The plane of a circular coil is horizontal. It has 10 turns each of radius 8cm. A current of 2 A flows through it. The current appears to flow clockwise from a point above the coil. Find the magnitude and direction of magnetic field at the centre of the coil due to the current.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA circular coil is lying in a horizontal plane. The coil has 20 turns with each turn of radius 10 cm. For an observer above the coil, the current of 5 A appears to flow in the anticlockwise direction. What is the magnitude and direction of magnetic field at the centre of the coil?
View SolutionIf a long horizontal conductor is bent as shown in figure and a current I is passed in it, find the magnitude and direction of magnetic field induction at the centre of circular part.
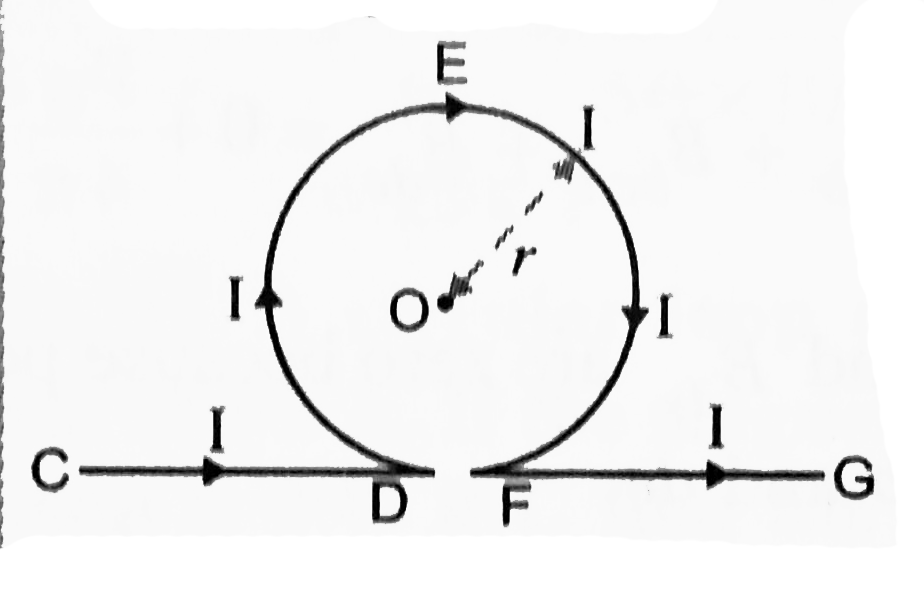 View Solution
View SolutionOne of the two identical conducting wires of length L is bent in the form of a circular loop and the other one into a circular coil of N identical turns. If the same current passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the central of the coil (BC), i.e. BLBC will be :
View SolutionA copper wire of length 7 metre is bent to form a circular loop. If i current flows through the loop, find out the magnitude of magnetic moment of the loop.
View Solution

