The plane of dip circle is set in the geographic meridian and the apparent dip is θ1. It is then set in a vertical plane perpendicular to the geographic meridian. Now, the apparent dip is θ2. The angle of declination θ at that place is
θ=tan−1(tanδ1tanδ2)
θ=tan−1(tanδ1+tanδ2)
θ=tan−1(tanδ1tanδ2)
θ=tan−1(tanδ1−tanδ2)
The correct Answer is:C
Here,tanδ1=VHcosθ
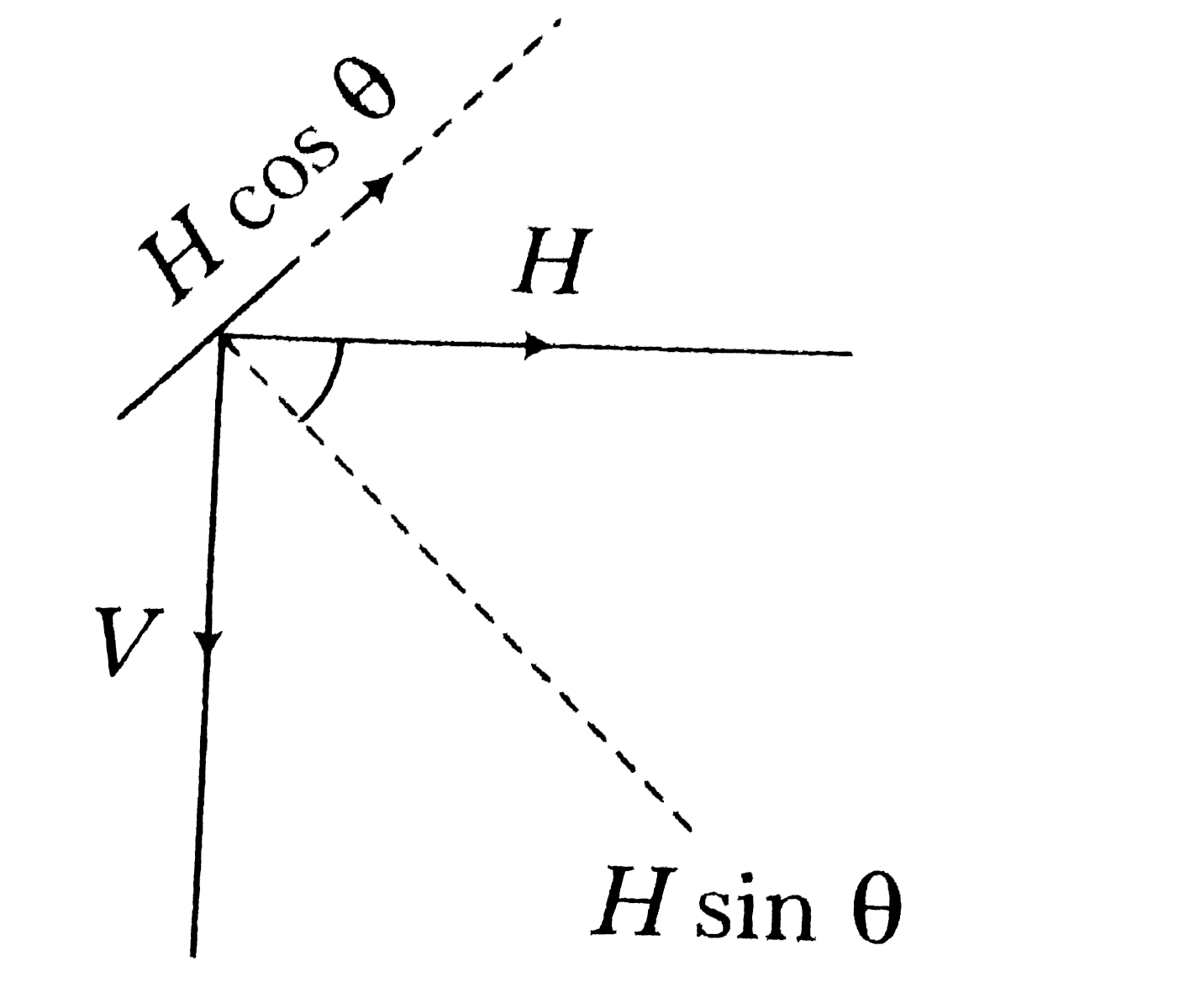
tanδ2=VHcos(90∘−θ)=VHsinθ
tanδ2tanδ2=sinθsinθ=tanθ
θ=tan−1(tanδ1tanδ2)
Similar Questions
A dip needle free to move in a vertical plane perpendiculr to the magneetic meridian will remain
View SolutionA dip circle is placed perpendicular to the magnetic meridian then thte magnetic needle will aligh
View SolutionA dip needle in a plane perpendicular to magnetic meridian will remain
View SolutionA dip circle is at right angles to the magnetic meridian. What will be the apparent dip ?
View SolutionAt 45∘ to the magnetic meridian, the apparent dip is 30∘. Find the true dip.
View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
View SolutionAparant angle of a dip is 30° in a plane at 45° from the magnetic meridian, then the true dip is
View SolutionA dip circle lying initially in the magnetic meridian is rotated through angle θin the horizontal plane. The ratio of tangent of apparent angle of dip to true angle of dip is
View SolutionA dip circle is at right angles to the magnetic meridian. What will be the apparent dip ?
View Solution
