The plot shows the position (x) as a function of time (t) for two trains that run on a parallel track. Train A is next to train B at t=0 and at t=T0.
At T0 both the trains have the same velocity.
Both the trains speed up all the times.
Both trains have the same velocity at some time before T0.
At T0 the trains have covered different distances
The correct Answer is:C
Initially slope of A is more than B and initially finally slope of A is less. So speed of A is initially more than finally less than B. So somewhere in between their speeds become the same.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
.Knowledge Check
The graph shows position as a function of time for two trains running on parallel tracks. Which statement is true ?
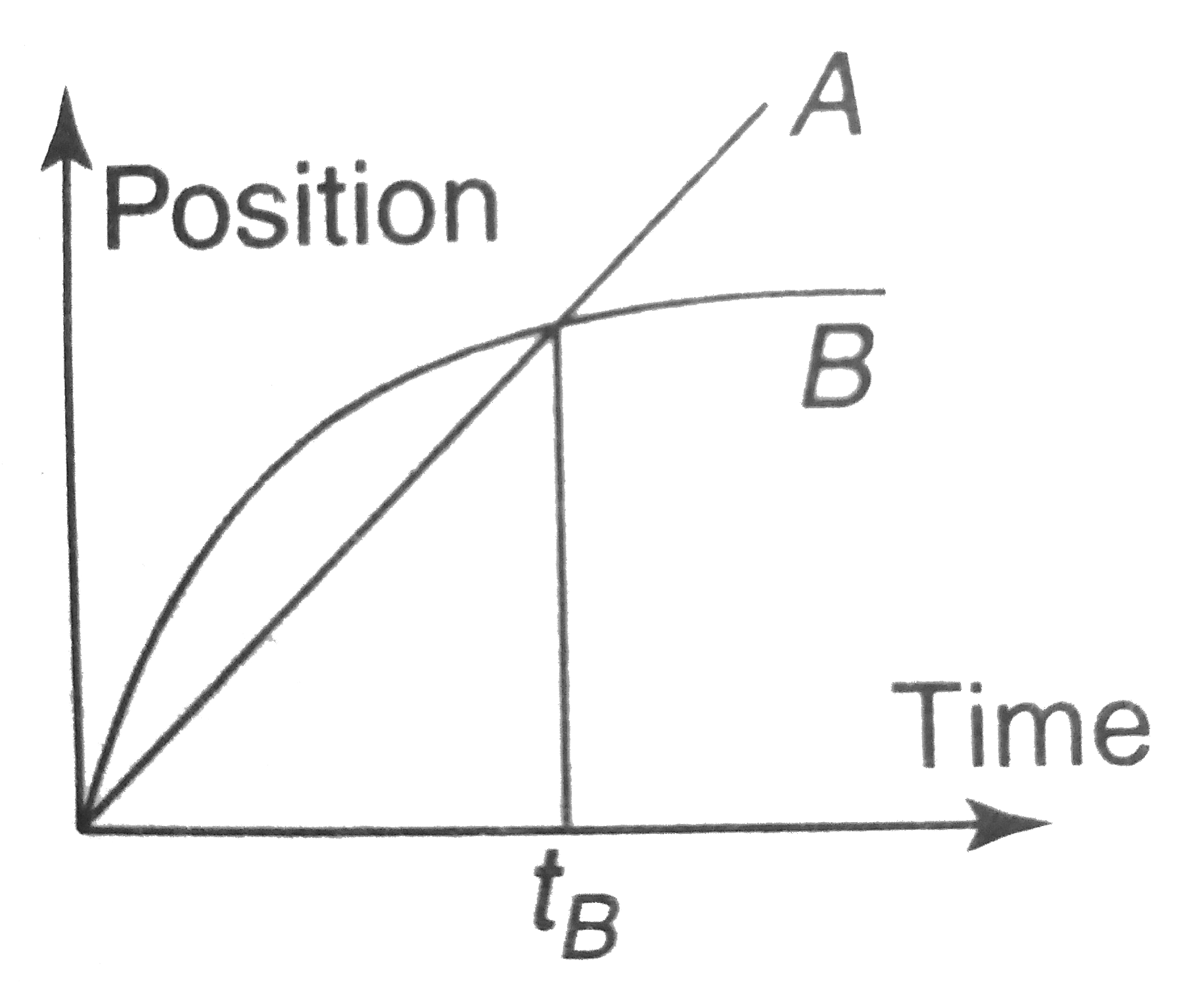AAt time tB, both trains have the same velocity.BBoth trains have the same velocity at some time after tBCBoth trains have the same velocity at some time before tB.DSomewhere on the graph, both trains have the same acceleration.A train of length L move with a constant speed Vt. A person at the back of the train fires a bullet at time t = 0 towards a target which is at a distance of D ( at time t = 0 ) from the front of the train ( on the same direction of motion ). Another person at the front of the train fires another bullet at time t = T towards the same target. Both bullets reach the target at the same time. Assuming the speed of the bullets Vb are same, the length of the train is
AT(Vb×2Vt)BT(Vb+Vt)C2T(Vb+2Vt)D2T(Vb−2Vt)
The instantaneous velocity of a particle moving in a straight line is given as a function of time by: v=v0(1−(tt0)n) where t0 is a constant and n is a positive integer . The average velocity of the particle between t=0 and t=t0 is 3v04.Then , the value of n is
View Solution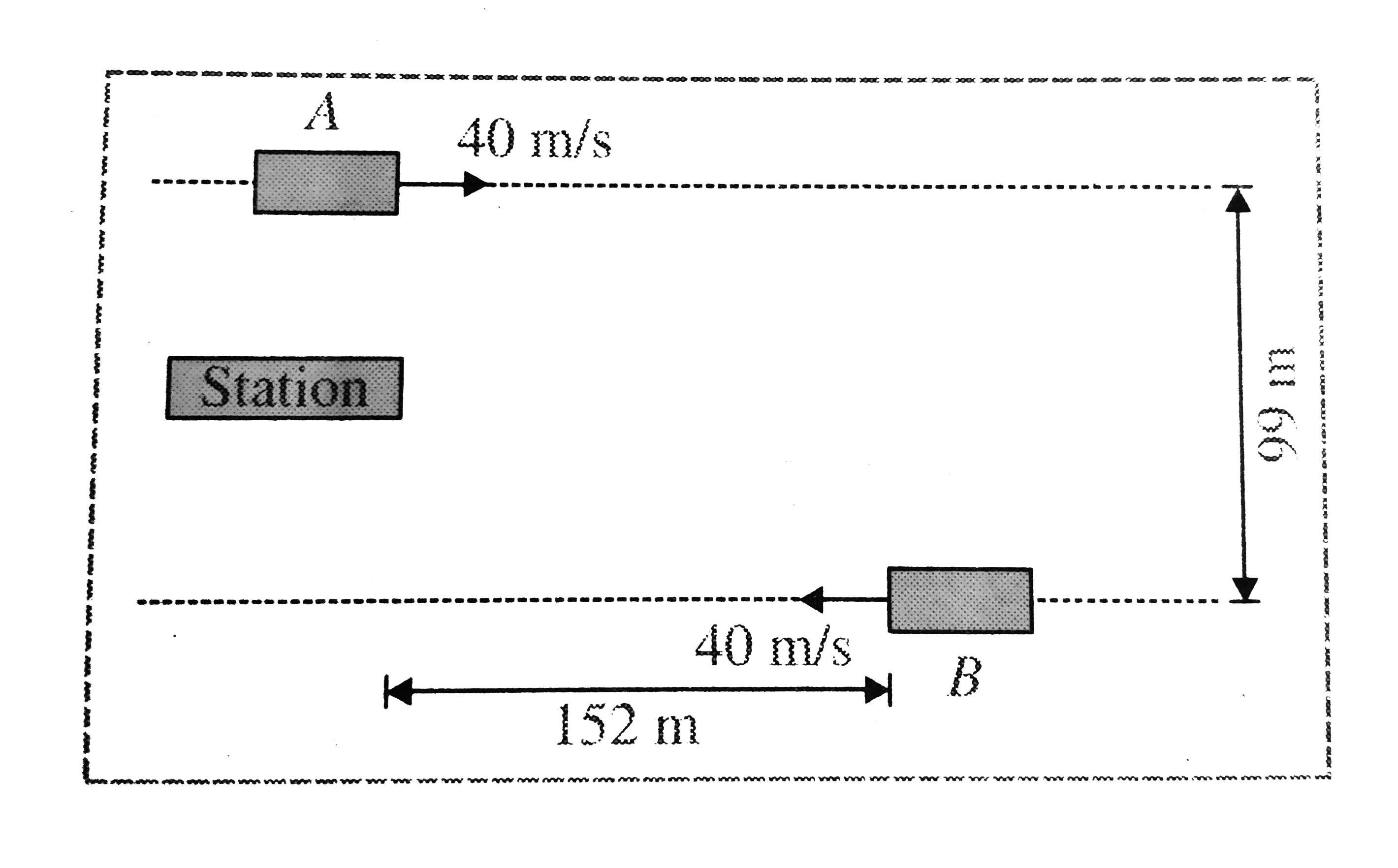
A train A crosses a station with a speed of 40 m/s and whitles a short pulse of natural frequency n0=596Hz another train B is approaching towards the same station with the same speed along a parallel track, Two track are d=99m apart. When train A whistles. train B is 152 m away from the station as shown in Fig. If velocity of sound in air is v=300ms. calculate frequency of the pulse heard by driver of train B.
View SolutionState the law of radioactive decay.
Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T12.
Depict in the plot the number of undecayed nuclei at (i) t=T12 and (ii) t=5T12.
View SolutionState the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half life T1/2
Depict in the plot the number of undecayed nuclei at
(i) t=3T1/2 and (ii) t=5T1/2.
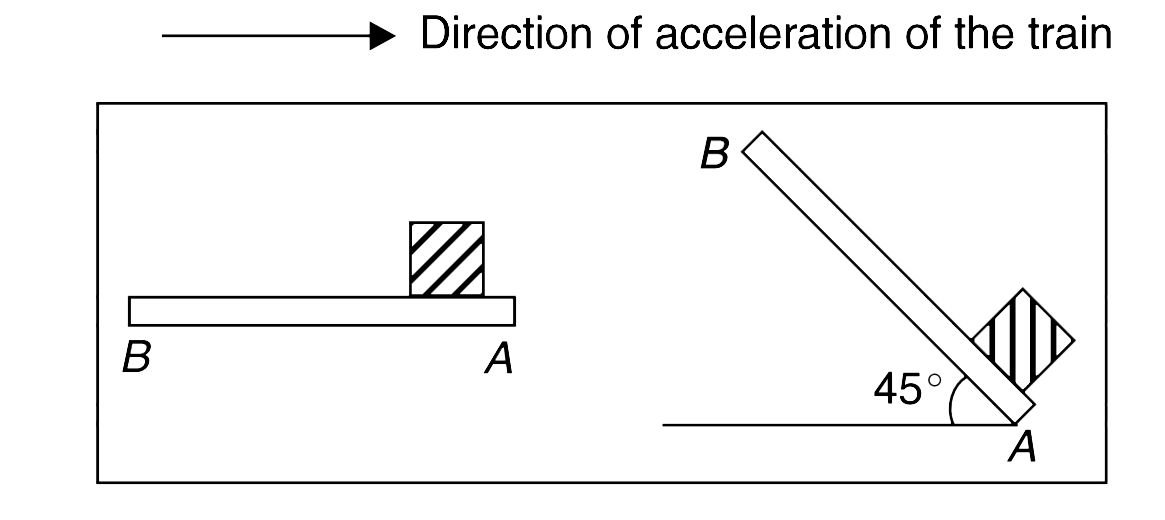
View SolutionAn experimenter is inside a uniformly accelerated train. Train is moving horizontally with constant acceleration a0. He places a wooden plank AB in horizontal position with end A pointing towards the engine of the train. A block is released at end A of the plank and it reaches end B in time t1. The same plank is placed at an inclination of 45∘ to the horizontal. When the block is released at A it now climbs to B in timet2. It was found that t2t1=254. What is the coefficient of friction between the block and the plank?
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae(−tt−xA)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View Solution