The position of a particle at any point instant is x . Find the velocity and acceleration at any instant .
To solve the problem of finding the velocity and acceleration of a particle whose position at any instant is given by x, we can follow these steps:
Step 1: Understand the Definition of Velocity
Velocity is defined as the rate of change of displacement with respect to time. Mathematically, it can be expressed as:
v=dxdt
where v is the velocity, x is the position of the particle, and t is time.
Step 2: Differentiate the Position Function
To find the velocity, we need to differentiate the position function x with respect to time t:
v=dxdt
This gives us the velocity of the particle at any instant.
Step 3: Understand the Definition of Acceleration
Acceleration is defined as the rate of change of velocity with respect to time. Mathematically, it can be expressed as:
a=dvdt
where a is the acceleration.
Step 4: Differentiate the Velocity Function
To find the acceleration, we need to differentiate the velocity function v with respect to time t:
a=dvdt=ddt(dxdt)
This is equivalent to taking the second derivative of the position function x:
a=d2xdt2
This gives us the acceleration of the particle at any instant.
Final Results
- The velocity of the particle at any instant is given by:
v=dxdt
- The acceleration of the particle at any instant is given by:
a=d2xdt2
Velocity is defined as the rate of change of displacement with respect to time. Mathematically, it can be expressed as:
v=dxdt
where v is the velocity, x is the position of the particle, and t is time.
To find the velocity, we need to differentiate the position function x with respect to time t:
v=dxdt
This gives us the velocity of the particle at any instant.
Acceleration is defined as the rate of change of velocity with respect to time. Mathematically, it can be expressed as:
a=dvdt
where a is the acceleration.
To find the acceleration, we need to differentiate the velocity function v with respect to time t:
a=dvdt=ddt(dxdt)
This is equivalent to taking the second derivative of the position function x:
a=d2xdt2
This gives us the acceleration of the particle at any instant.
- The velocity of the particle at any instant is given by:
v=dxdt
- The acceleration of the particle at any instant is given by:
a=d2xdt2
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - LONG ANSWER QUESTIONS
5 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - EXAMPLES
26 Videos
- UNITSBOOK - ICSECHAPTER - UNITSEXERCISE - MODULE 3 (SELECTED PROBLEMS)
38 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - From Musical Sound
10 Videos
Similar Questions
Assertion A particle is roting in a circle of radius 1 m. At some given instant, its speed is 2ms−1. Then acceleration of particle at the given instant is 4ms−2.
Reason Centripetal acceleration at this instant is 4ms−2 towards centre of circle.
View SolutionFor a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then
View Solution
Knowledge Check
Assertion : A particle may be momentarily at rest and yet have non-zero acceleration.
Reason : The zero velocity of a particle at any instant does not necessarily imply zero acceleration at that instant.AIf both assertion and reason are trure and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanations of assertion.CIf assertion is true but reason is false.DIf both assertion and reason is false
Figure shows path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram can not be true in any situation? (In each figure velocity is tangential to the trajectory).
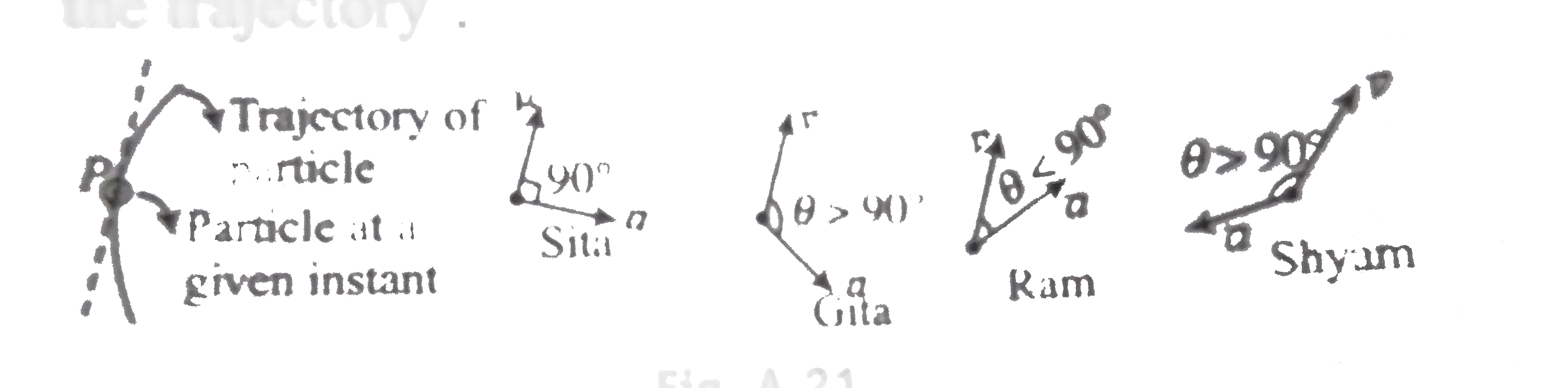
View SolutionFigure shows a path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram cannot be true in any situation? (In each figure, velocity is tangential to the trajectory).

View SolutionMark the correct statements for a particle go ing on a straight line:
(a) If the velocity and acceleration have opposite sign, the object is slowing down.
(b) If the position and velocity have opposite sign, the particle is moving towards the origin.
(c) If the velocity is zero at an instant, the acceleration should also be zero at that instant.
(d) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.
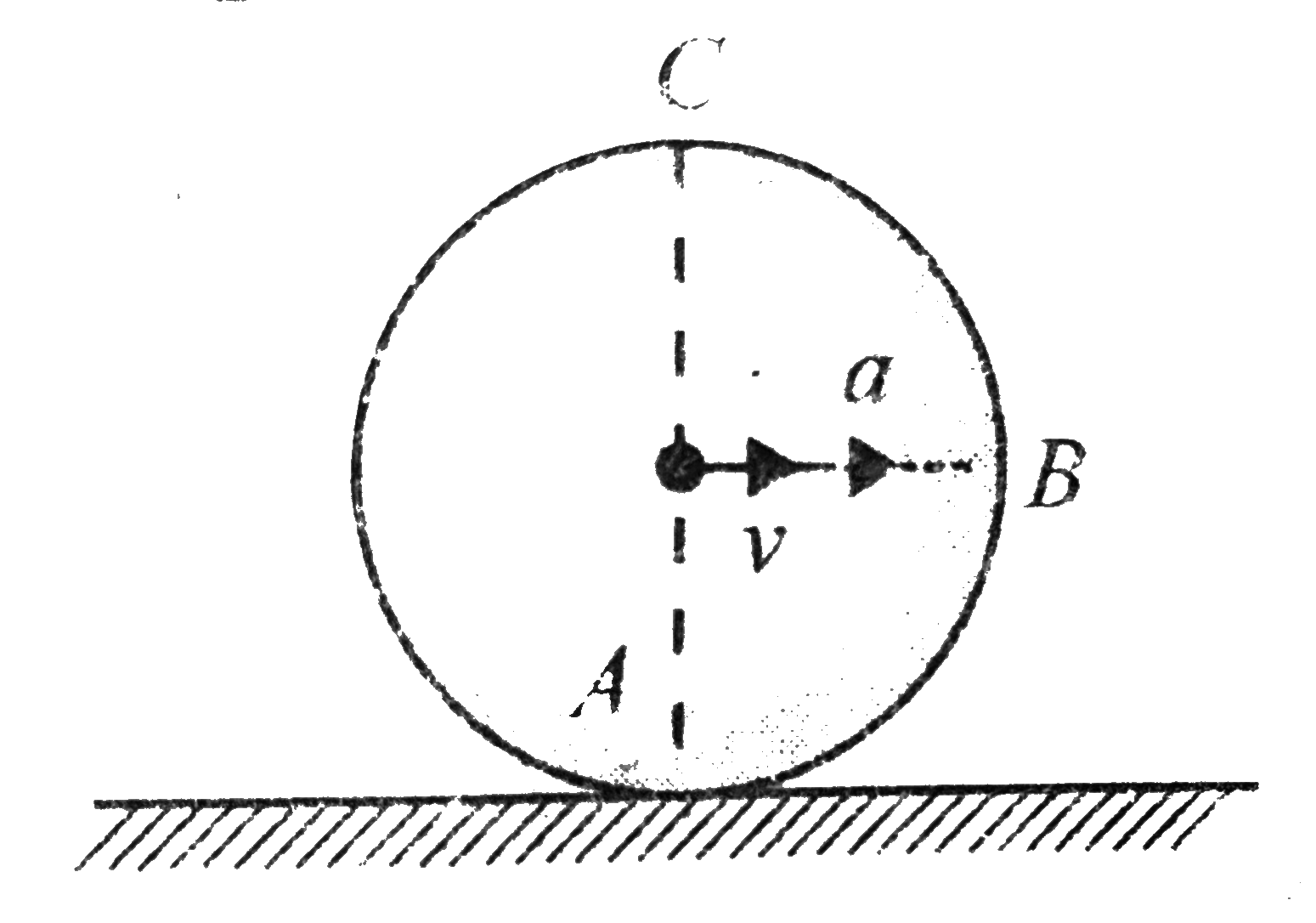
View SolutionA wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
View SolutionA particle performs linear S.H.M. At a particular instant, velocity of the particle is u and acceleration is α while at another instant, velocity is v and acceleration β (0<α<β). The distance between the two position is
View SolutionA solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity ω. Its radius is R. Find the angular acceleration at that instant mass of sphere is m

View SolutionIf x is the displacement of a simple harmonic oscillator at a certain instant and y its acceleration at that instant, draw graph of (x, y) at all instant in one complete oscillation,
View Solution
