Doubtnut Promotions Sticky

The potential energy function for a particle executing simple harmonic motion is given by V ( x ) = 1 2 k x 2 , where k is the force constant of the oscillatore. For k = 1 2 N m - 1 , show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x = ± 2 m .

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

At any instant, the total energy of an oscillator is the sum of K.E. and P.E.
i.e. E = K . E . + P . E . = 1 2 m u 2 + 1 2 k x 2
The particle turns back at the instant, when its velocity becomes zero i.e. u = 0 .
∴ E = 0 + 1 2 k x 2
As E = 1 joule and k = 1 2 N / m ∴ 1 = 1 2 × 1 2 x 2 or x 2 = 4 , x = ± 2 m

|
Updated on:21/07/2023
Class 11PHYSICSWORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
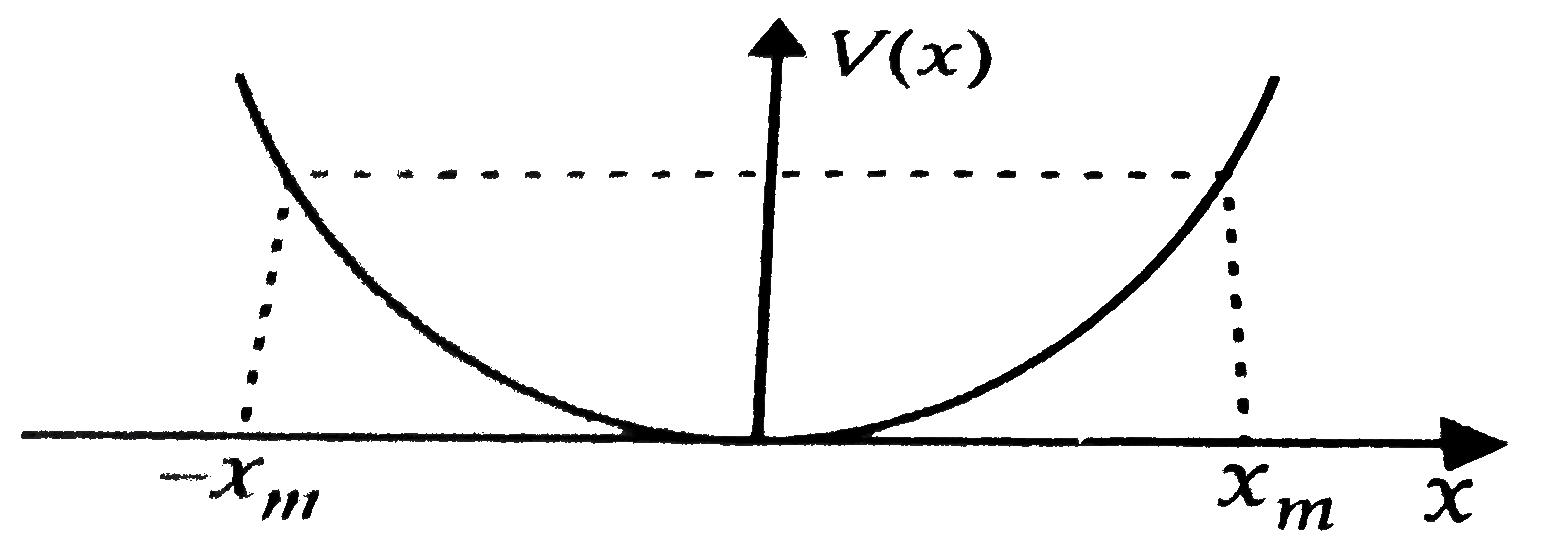    ocr_image

    AV=0, K=E
    BV=E, K=0
    CV lt K, K=0
    DV=0, K lt E
  • Question 2 - Select One

    The potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to

    A√x
    Bx
    Cx2
    Dx3
  • Question 3 - Select One

    The total energy of a particle, executing simple harmonic motion is.
    where x is the displacement from the mean position, hence total energy is independent of x.

    A(a) independent of x.
    B(b) ∝x2
    C(c ) prop x
    D(d) propx^(1//2)