The potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
−3k
+3k
k
None of these
The correct Answer is:A
To solve the problem, we need to calculate the work done by the conservative force when moving a particle from the point (1, 1) to (2, 3) using the given potential energy function U=k(x+y).
1. Identify the Initial and Final Points:
- Initial point (x1,y1)=(1,1)
- Final point (x2,y2)=(2,3)
2. Calculate the Initial Potential Energy Ui:
- Using the potential energy function U=k(x+y):
Ui=k(1+1)=k⋅2=2k
3. Calculate the Final Potential Energy Uf:
- For the final point (2,3):
Uf=k(2+3)=k⋅5=5k
4. Calculate the Change in Potential Energy ΔU:
- The change in potential energy is given by:
ΔU=Uf−Ui=5k−2k=3k
5. Calculate the Work Done by the Conservative Force:
- The work done by the conservative force is the negative of the change in potential energy:
W=−ΔU=−3k
Final Answer:
The work done by the conservative force in moving the particle from (1, 1) to (2, 3) is −3k.
---
- Initial point (x1,y1)=(1,1)
- Final point (x2,y2)=(2,3)
- Using the potential energy function U=k(x+y):
Ui=k(1+1)=k⋅2=2k
- For the final point (2,3):
Uf=k(2+3)=k⋅5=5k
- The change in potential energy is given by:
ΔU=Uf−Ui=5k−2k=3k
- The work done by the conservative force is the negative of the change in potential energy:
W=−ΔU=−3k
The work done by the conservative force in moving the particle from (1, 1) to (2, 3) is −3k.
Similar Questions
The potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View SolutionIn a two dimensional space the potential energy function for a conservative force acting on a particle of mass m = 0.1 kg is given by U = 2 (x + y) joule (x and y are in m). The particle is being moved on a circular path at a constant speed of V=1ms−1. The equation of the circular path is x2+y2=42. (a) Find the net external force (other than the conservative force) that must be acting on the particle when the particle is at (0, 4). (b) Calculate the work done by the external force in moving the particle from (4, 0) to (0, 4).
View Solution
Knowledge Check
- Question 1 - Select One or More
The potential energy of a particle moving along x-axis is given by U=20+5sin(4πx), where U is in J and x is in metre under the action of conservative force :
Aif total mechanical energy is 20J,
then at x=7/8m, particle is at equilibriumBif total mechanical energy is 20J,
then at x=7/8m particle is not at equilibriumCif total mechanical energy is 20J,
then at x=3/8m, particle is at equilibriumDif total mechanical energy is 20J,
then at x=3/8m, particle is not at equilibrium. - Question 2 - Select One
A particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
AF0ω(1−cosω)BF02ω(1−cos2ω)C2F0sin2ωωDF0ω(1+cos2ω) - Question 3 - Select One
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
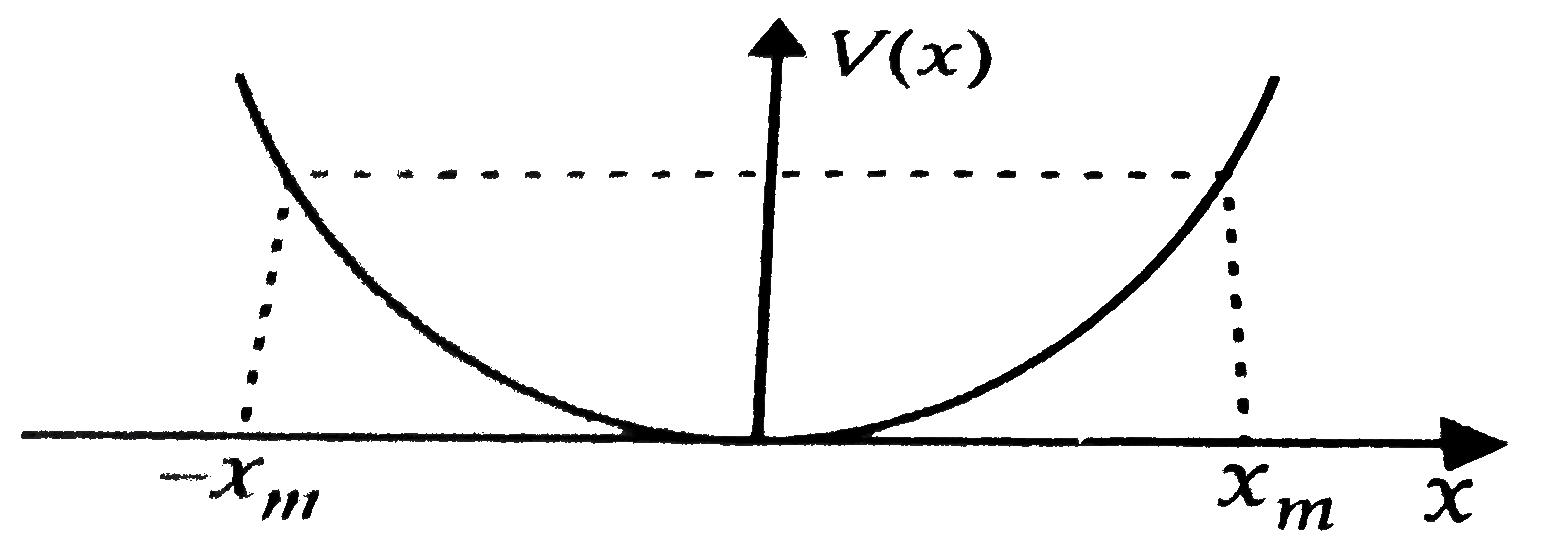 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
The potential energy of a partical of mass 2kg moving in y−z plane is given by U=(−3y+4z)J where y and z are in metre. The magnitude of force ( in newton ) on the particle is :
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy U in joule of a particle of mass 1kg moving in x−y plane obeys the lawU=3x+4y, where (x,y) are the co-ordinates of the particle in metre. If the particle is at rest at (6,4) at time t=0 then :
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View Solution

