The potential energy function for a particle executing simple harmonic motion is given by $V (x) = \frac{1}{2} k x^{2}$ , where k is the force constant of the oscillatore. For $k = \frac{1}{2} N m^{- 1}$ , show that a particle of total energy 1 joule moving under this potential must turn back when it reaches $x = \pm 2 m .$

Video Solution

Text Solution

Verified by Experts

The potential energy of the aprticle
$= V = \frac{1}{2} k x^{2}$
$k = \frac{1}{2} N / m^{- 1}$
$V = \frac{1}{2} \times \frac{1}{2} x^{2} = \frac{1}{4} x^{2}$

When total energy $= P . E + K . E = 1 J$
As the oscillating particle turns back at the point where its velocity = 0
Therefore , K.E = 0
Therefore , total energy = P.E
So, $\frac{1}{4} x^{2} = 1$
$x^{2} = 4$
$x = \pm 2$
Hence , it can be said that particle must turn back when it reaches $x = \pm 2$ m .

Updated on:21/07/2023

The potential energy function for a particle executing linear SHM is given by $V (x) = \frac{1}{2} k x^{2}$ where k is the force constant of the oscillator. For $k = 0.5 N m^{- 1}$ , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches $x = \pm x_{m}$ .if V and K indicate the potential energy and kinetic energy respectively of the particle at $x = + x_{m}$ ,then which of the following is correct?

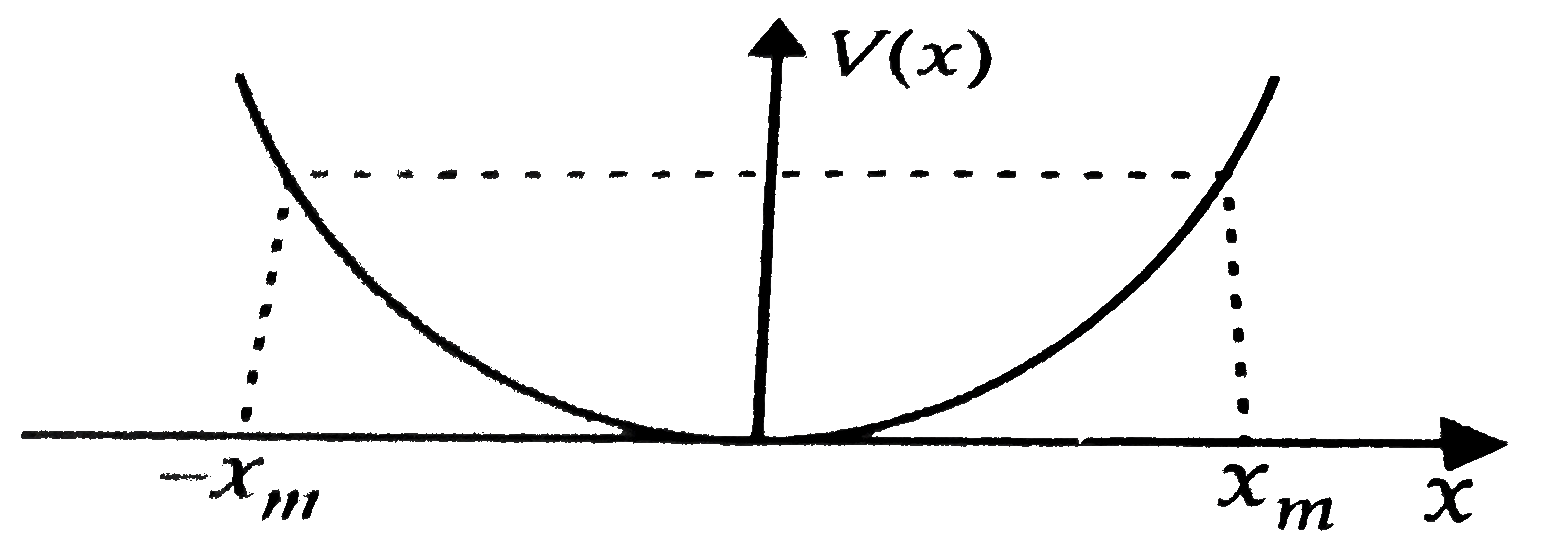AV=0, K=E
BV=E, K=0
CV lt K, K=0
DV=0, K lt E
The potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
A $\sqrt{x}$
Bx
C $x^{2}$
D $x^{3}$
The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
A(a) independent of x.
B(b) $\propto x^{2}$
C(c ) prop x
D(d) propx^(1//2)