The potential energy (in SI units) of a particle of mass 2kg in a conservative field is U=6x−8y. If the initial velocity of the particle is →u=−1.5ˆi+2ˆj, then find the total distance travelled by the particle in the first two seconds.
The correct Answer is:15m
To solve the problem step by step, we will follow the outlined approach in the video transcript.
Step 1: Determine the Force from Potential Energy
The potential energy U is given as:
U=6x−8y
To find the force →F, we use the relationship between force and potential energy:
→F=−∇U=−(∂U∂x^i+∂U∂y^j)
Calculating the partial derivatives:
∂U∂x=6and∂U∂y=−8
Thus, the force vector becomes:
→F=−(6^i−8^j)=−6^i+8^j
Step 2: Calculate the Acceleration
Using Newton's second law, we can find the acceleration →a:
→a=→Fm
Given that the mass m=2kg:
→a=−6^i+8^j2=−3^i+4^j
Step 3: Initial Velocity
The initial velocity →u is given as:
→u=−1.5^i+2^j
Step 4: Determine the Distance Traveled
Since the acceleration is constant and the motion is in a straight line, we can use the equation of motion:
→s=→ut+12→at2
We need to calculate the distance traveled in the first 2 seconds (t=2s):
→s=(−1.5^i+2^j)(2)+12(−3^i+4^j)(22)
Calculating each term:
1. Initial velocity term:
→ut=(−1.5^i+2^j)(2)=−3^i+4^j
2. Acceleration term:
12→at2=12(−3^i+4^j)(4)=(−6^i+8^j)
Combining both terms:
→s=(−3^i+4^j)+(−6^i+8^j)=(−9^i+12^j)
Step 5: Calculate the Magnitude of the Displacement
To find the total distance traveled, we calculate the magnitude of the displacement vector:
|→s|=√(−9)2+(12)2=√81+144=√225=15m
Final Answer
The total distance traveled by the particle in the first two seconds is:
15m
The potential energy U is given as:
U=6x−8y
To find the force →F, we use the relationship between force and potential energy:
→F=−∇U=−(∂U∂x^i+∂U∂y^j)
∂U∂x=6and∂U∂y=−8
Thus, the force vector becomes:
→F=−(6^i−8^j)=−6^i+8^j
Using Newton's second law, we can find the acceleration →a:
→a=→Fm
Given that the mass m=2kg:
→a=−6^i+8^j2=−3^i+4^j
The initial velocity →u is given as:
→u=−1.5^i+2^j
Since the acceleration is constant and the motion is in a straight line, we can use the equation of motion:
→s=→ut+12→at2
We need to calculate the distance traveled in the first 2 seconds (t=2s):
→s=(−1.5^i+2^j)(2)+12(−3^i+4^j)(22)
1. Initial velocity term:
→ut=(−1.5^i+2^j)(2)=−3^i+4^j
2. Acceleration term:
12→at2=12(−3^i+4^j)(4)=(−6^i+8^j)
→s=(−3^i+4^j)+(−6^i+8^j)=(−9^i+12^j)
To find the total distance traveled, we calculate the magnitude of the displacement vector:
|→s|=√(−9)2+(12)2=√81+144=√225=15m
The total distance traveled by the particle in the first two seconds is:
15m
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
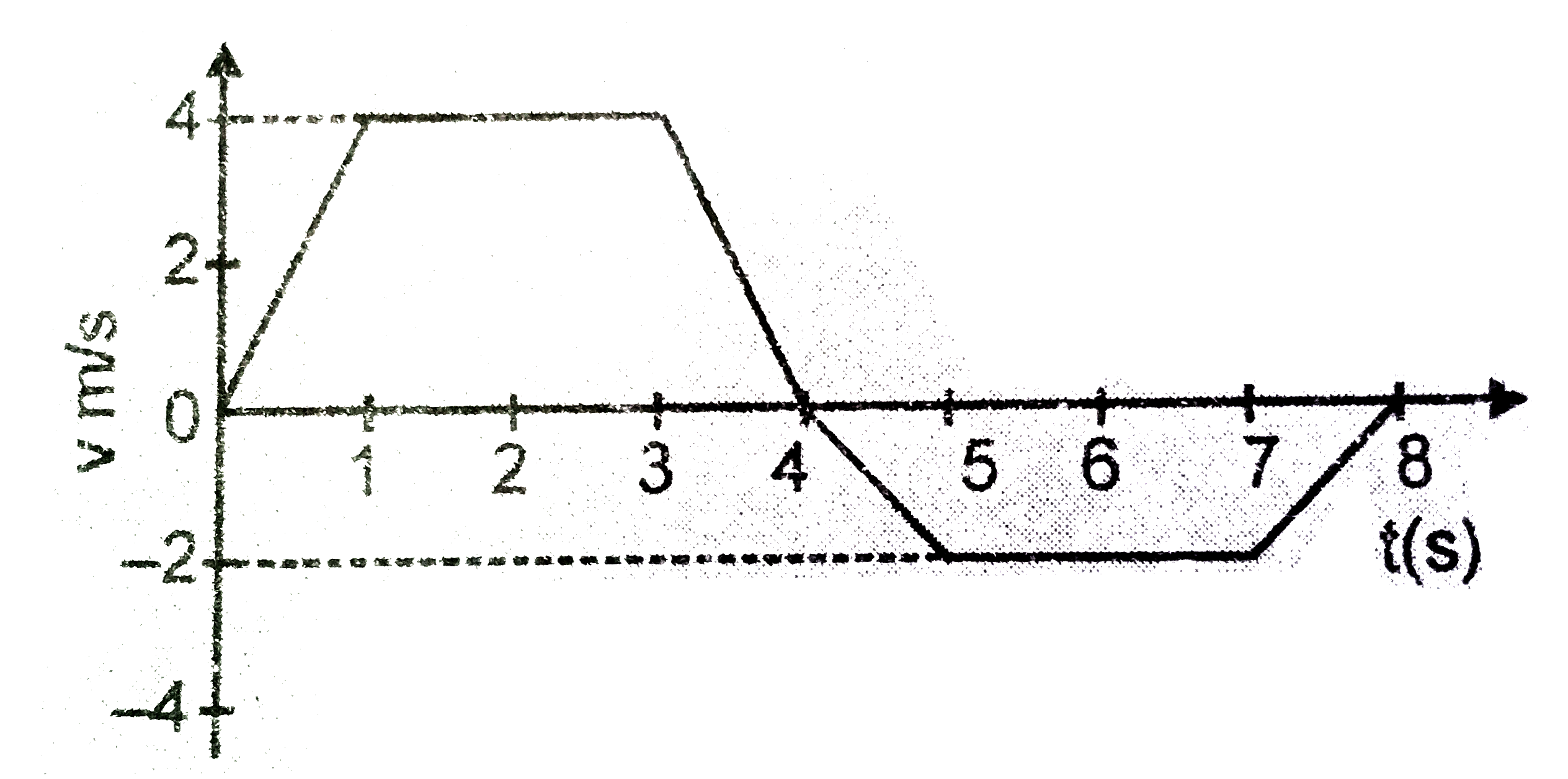
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
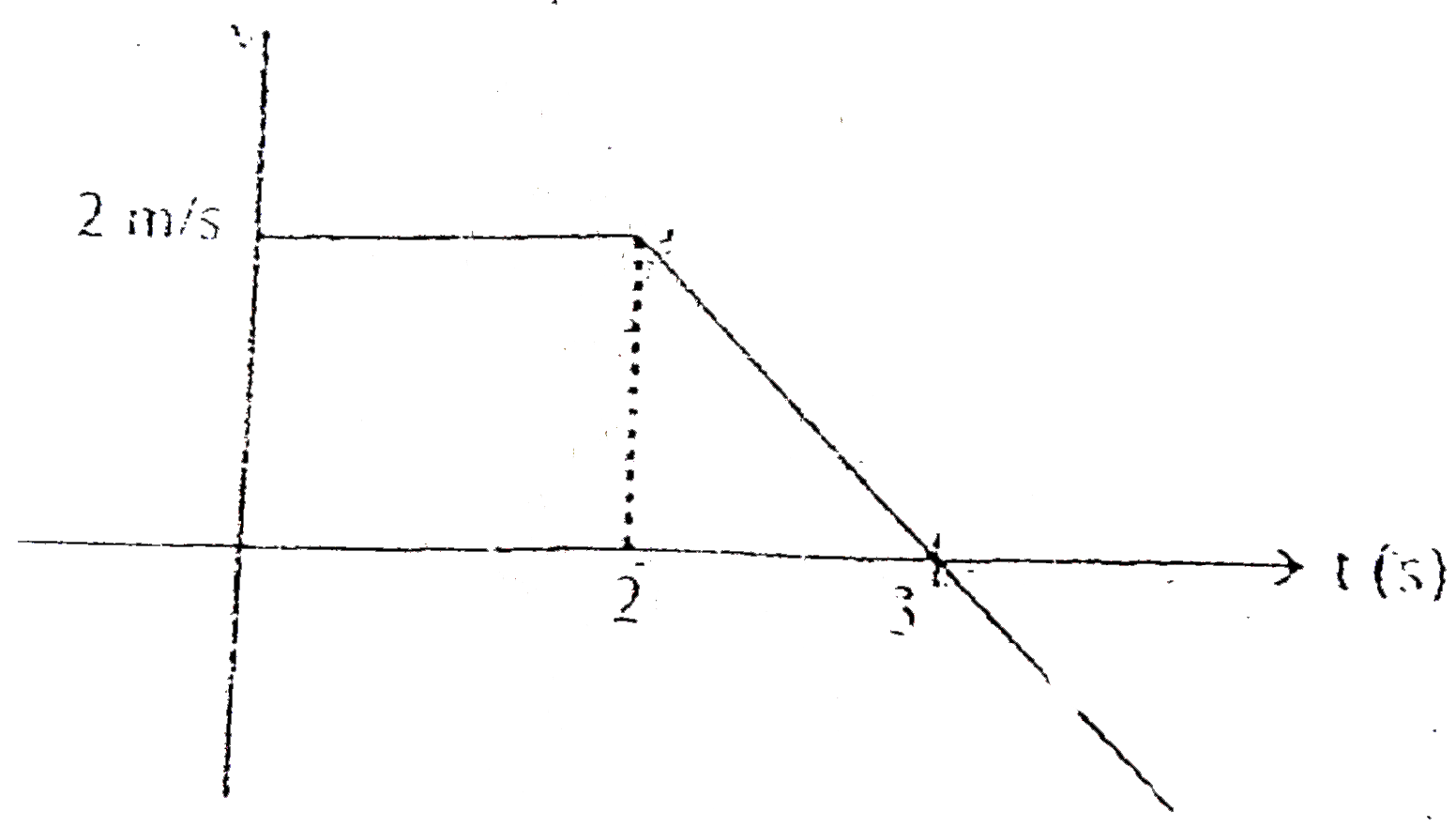
View SolutionA particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe potential energy of a particle of mass 2 kg moving in a plane is given by U=(−6x−8y)J. The position coordinates x and y are measured in meter. If the particle is initially at rest at position (6, 4)m, then
View Solution
