The pressure P1anddensityd1 of a diatomic gas (γ=75) change to P2andd2 during an adiabatic operation .If d2d1=32,thenP2P1is
a. 76
b. 128
c. 168
d. 298
The correct Answer is:B
To solve the problem, we need to find the ratio P2P1 given that the density ratio d2d1=32 and the gas is diatomic with γ=75.
1. Understand the Adiabatic Process:
For an adiabatic process, the relationship between pressure P and density d can be expressed as:
P⋅Vγ=constant
where γ is the heat capacity ratio.
2. Relate Volume and Density:
Since volume V is related to density d by the equation V=md (where m is the mass, which is constant), we can rewrite the adiabatic condition in terms of density:
P⋅(md)γ=constant
This leads to:
P⋅d−γ=constant
or
P∝dγ
3. Set Up the Ratios:
From the proportionality, we can write:
P1P2=(d1d2)γ
4. Substitute the Given Density Ratio:
We know d2d1=32, which means:
d1d2=132
Therefore, substituting this into the equation gives:
P1P2=(132)75
5. Calculate the Power:
Now, calculate (132)75:
P1P2=13275
Since 32=25, we can rewrite this as:
3275=(25)75=27
Thus:
P1P2=127
6. Reciprocate to Find P2P1:
To find P2P1, we take the reciprocal:
P2P1=27=128
Final Answer:
P2P1=128
For an adiabatic process, the relationship between pressure P and density d can be expressed as:
P⋅Vγ=constant
where γ is the heat capacity ratio.
Since volume V is related to density d by the equation V=md (where m is the mass, which is constant), we can rewrite the adiabatic condition in terms of density:
P⋅(md)γ=constant
This leads to:
P⋅d−γ=constant
or
P∝dγ
From the proportionality, we can write:
P1P2=(d1d2)γ
We know d2d1=32, which means:
d1d2=132
Therefore, substituting this into the equation gives:
P1P2=(132)75
Now, calculate (132)75:
P1P2=13275
Since 32=25, we can rewrite this as:
3275=(25)75=27
Thus:
P1P2=127
To find P2P1, we take the reciprocal:
P2P1=27=128
P2P1=128
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The pressure and density of a diatomic gas (γ=7/5) change adiabatically from (p,d) to (p′,d′). If d′d=32, then P′P should be
View SolutionThe pressure and density of a diatomic gas (γ=75) change adiabatically from (P,d) to P',d'). If d'd=32, then find the value of P'P ?
View SolutionThe pressure and density of a gas (Ƴ =5/3) changes adiabatically from (p1,d1 ) to (p2,d2).If d2/d1=27 the find value of p2/p1 ?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
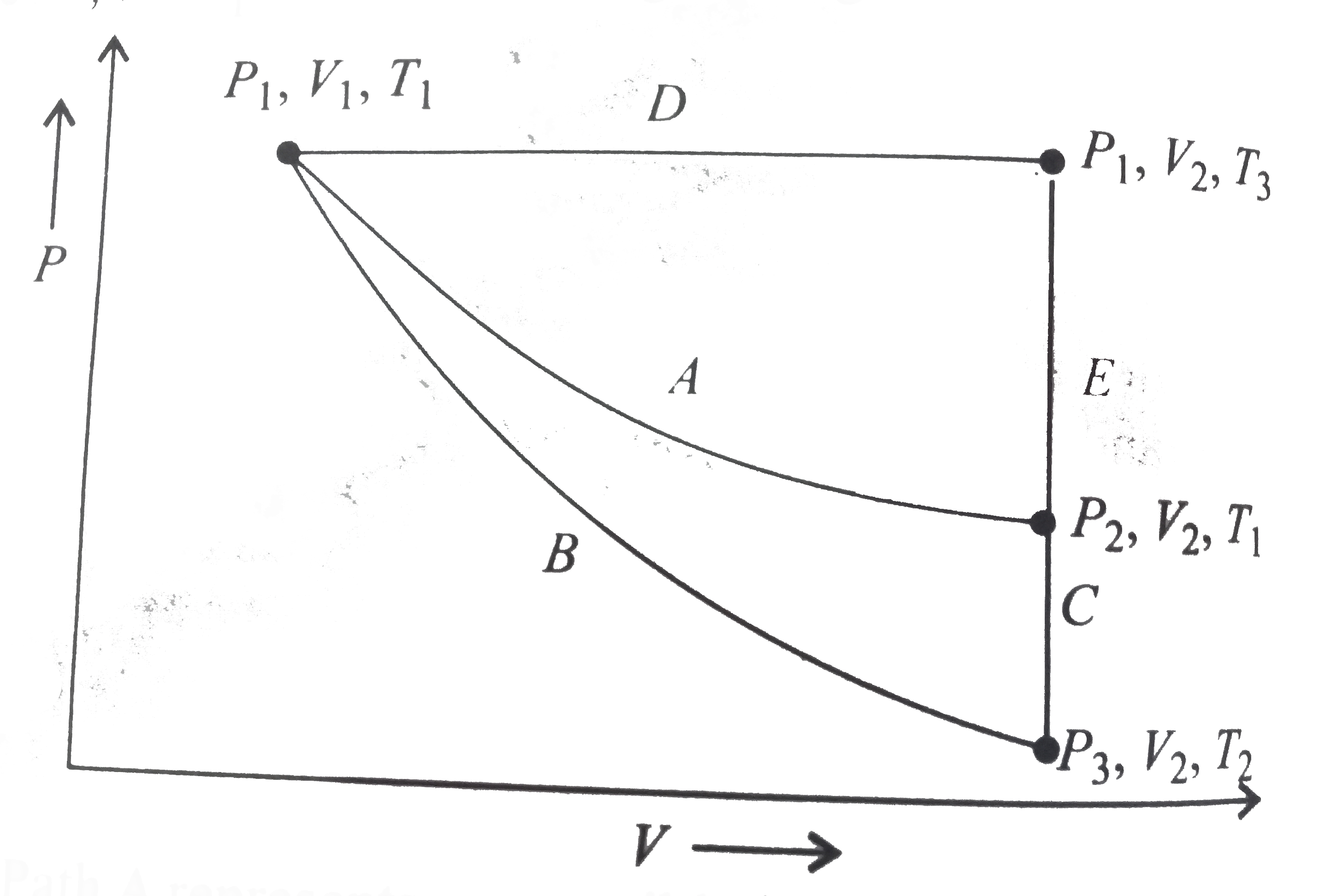
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
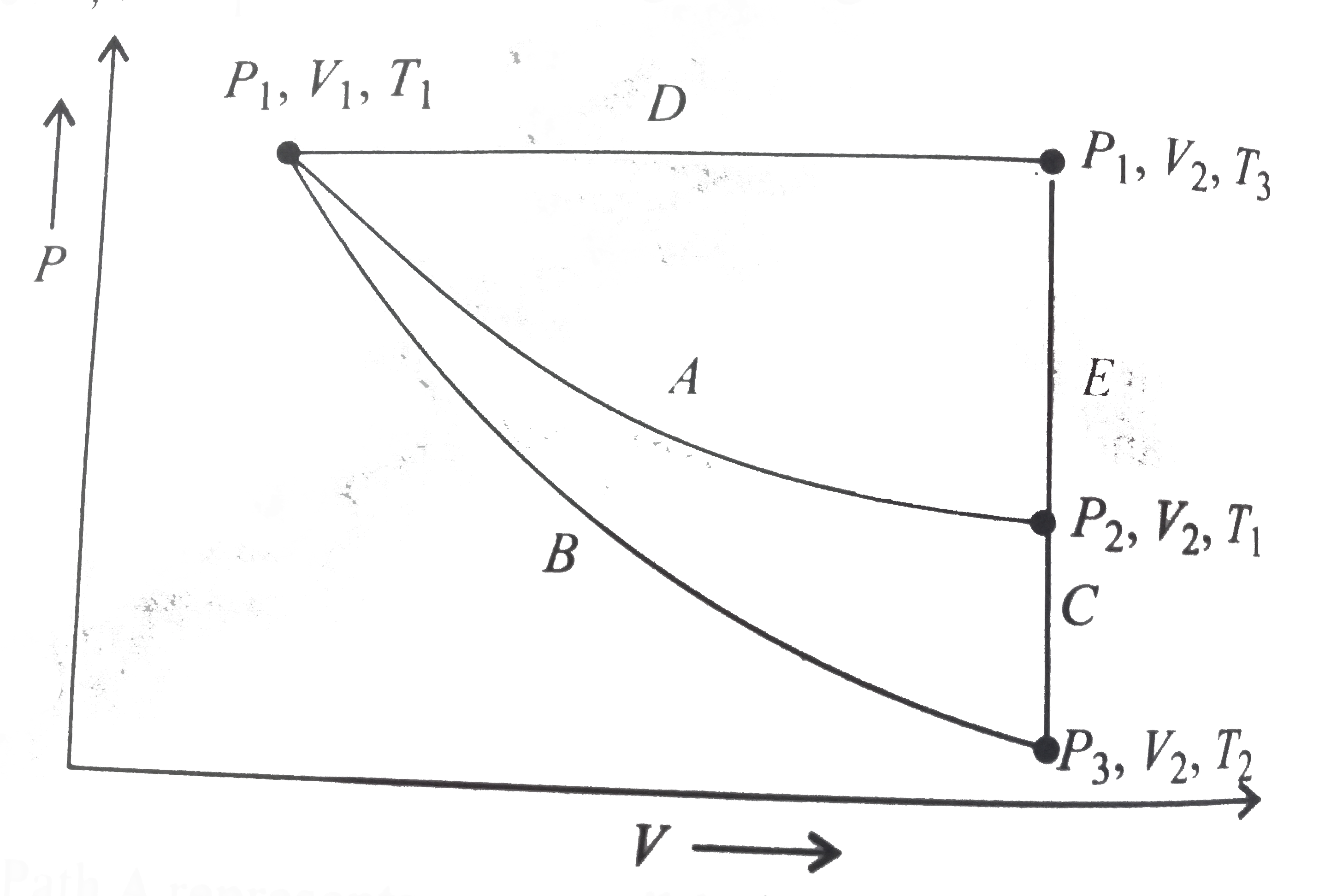
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
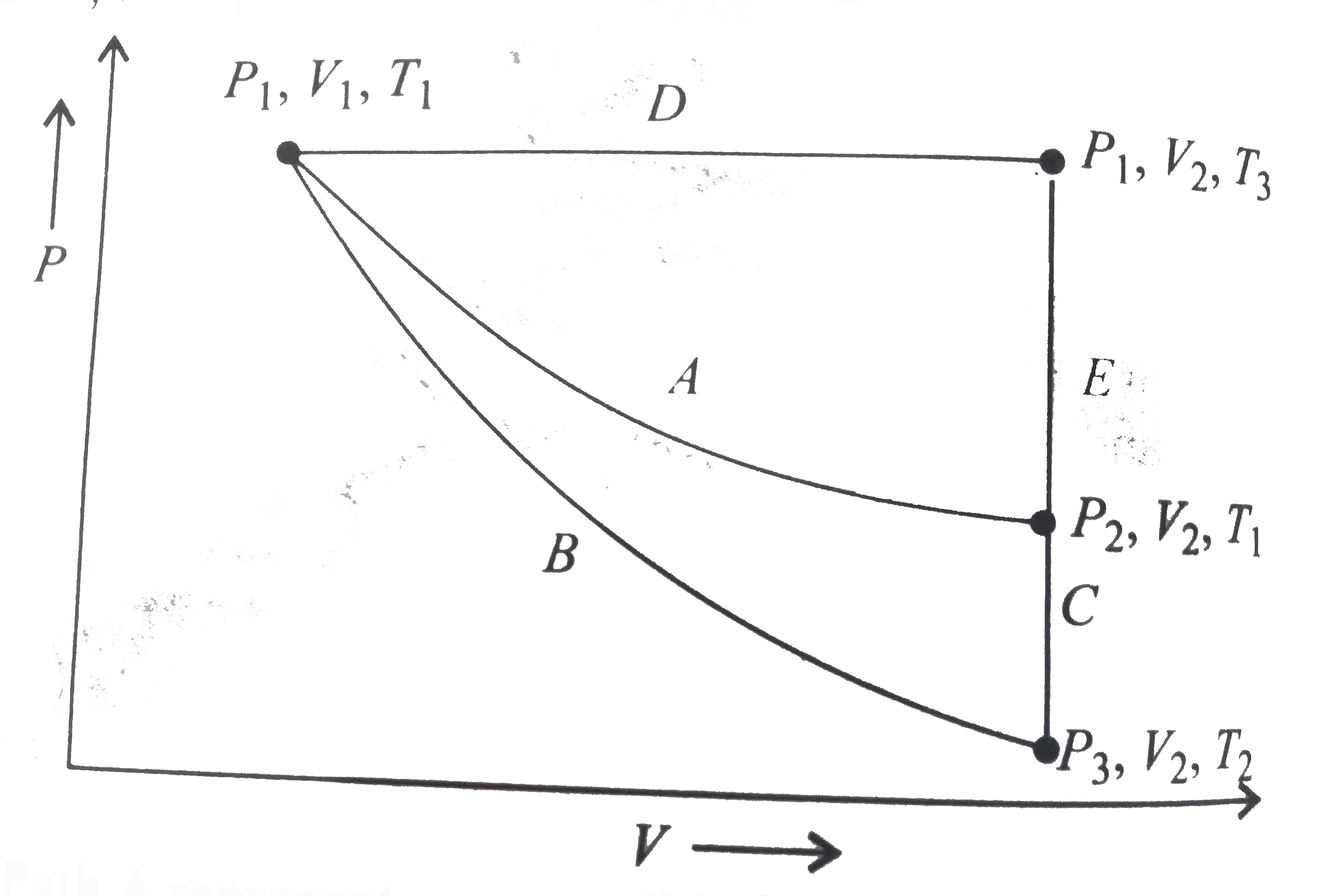
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
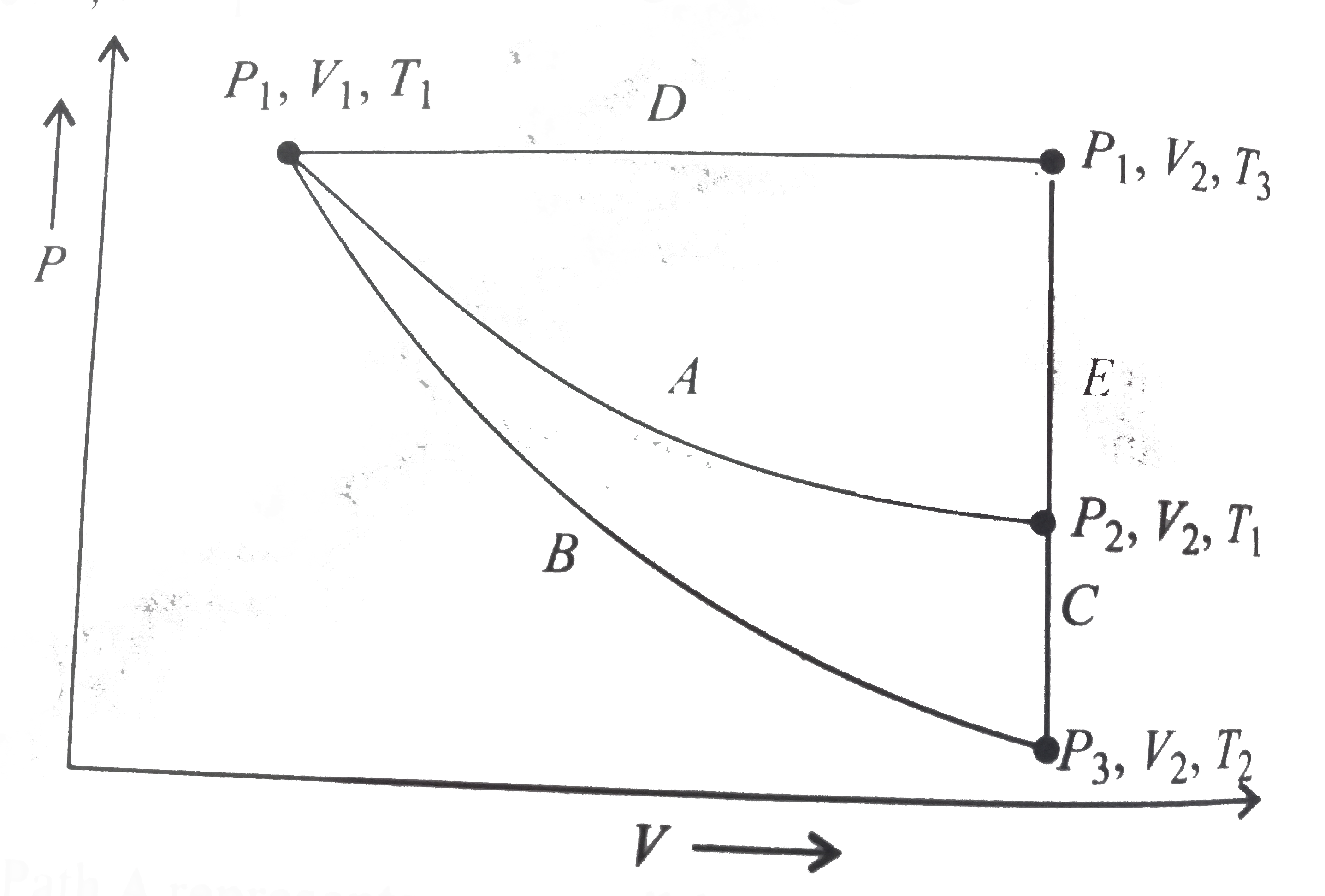
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
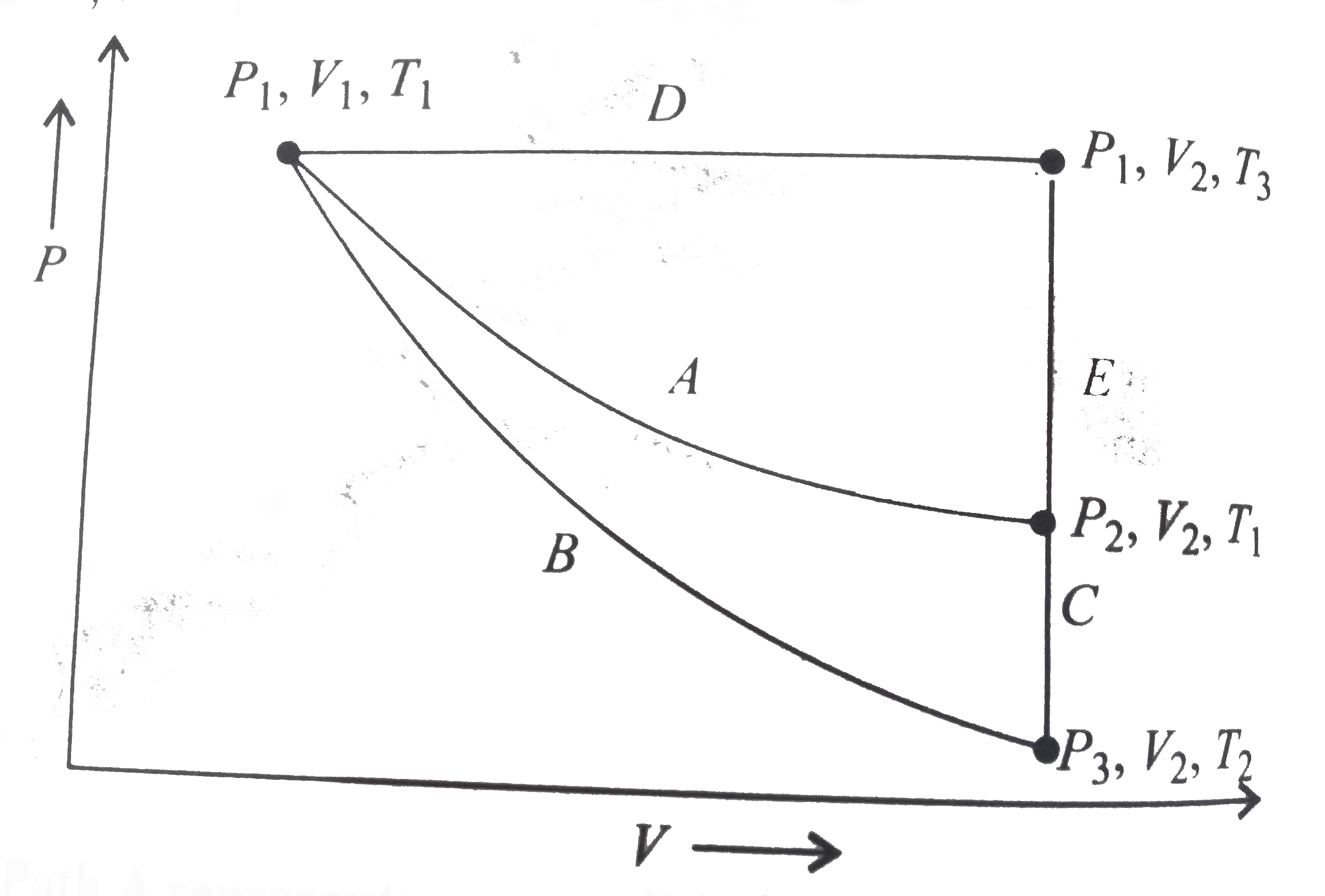
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View Solution
