For an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
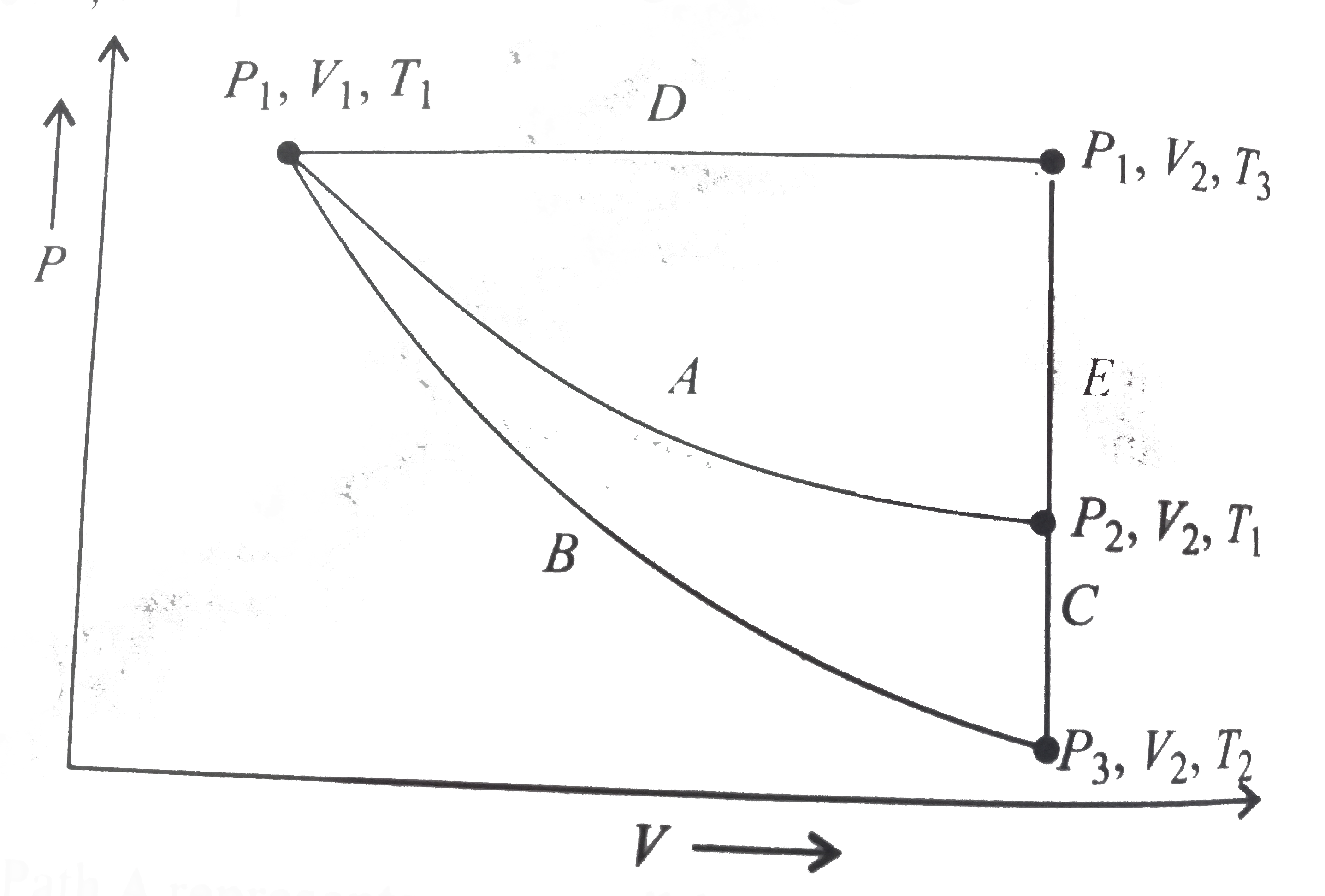
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
nRInV2V1
−nRInV2V1
zero
nRT1InV2V1
Path (B+C) occurs in adiabatic conditions
∴Q=0
We know that
ΔS=qrevT
∴Qrev=TΔS
∴Qrev=nRInV2V1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Multiple Correct)
50 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type
2 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Paragraph for Problem
1 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Select the correct statement
View SolutionWhich is an irreversible process ?
View SolutionThree moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00 bar. The initial and final volumes of the gas are 10.0L and 30.0L, respectively. ltbr> Change in entropy of the universe is
View SolutionIn the analysis of 0.1 of sample of feldspar, 0.118 g of mixture of NaCl and KCl is obtained which on treatment with AgNO3 gives 0.2451 of AgCl. Calculate the precentage of Na2O and K2O in feldspar.
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
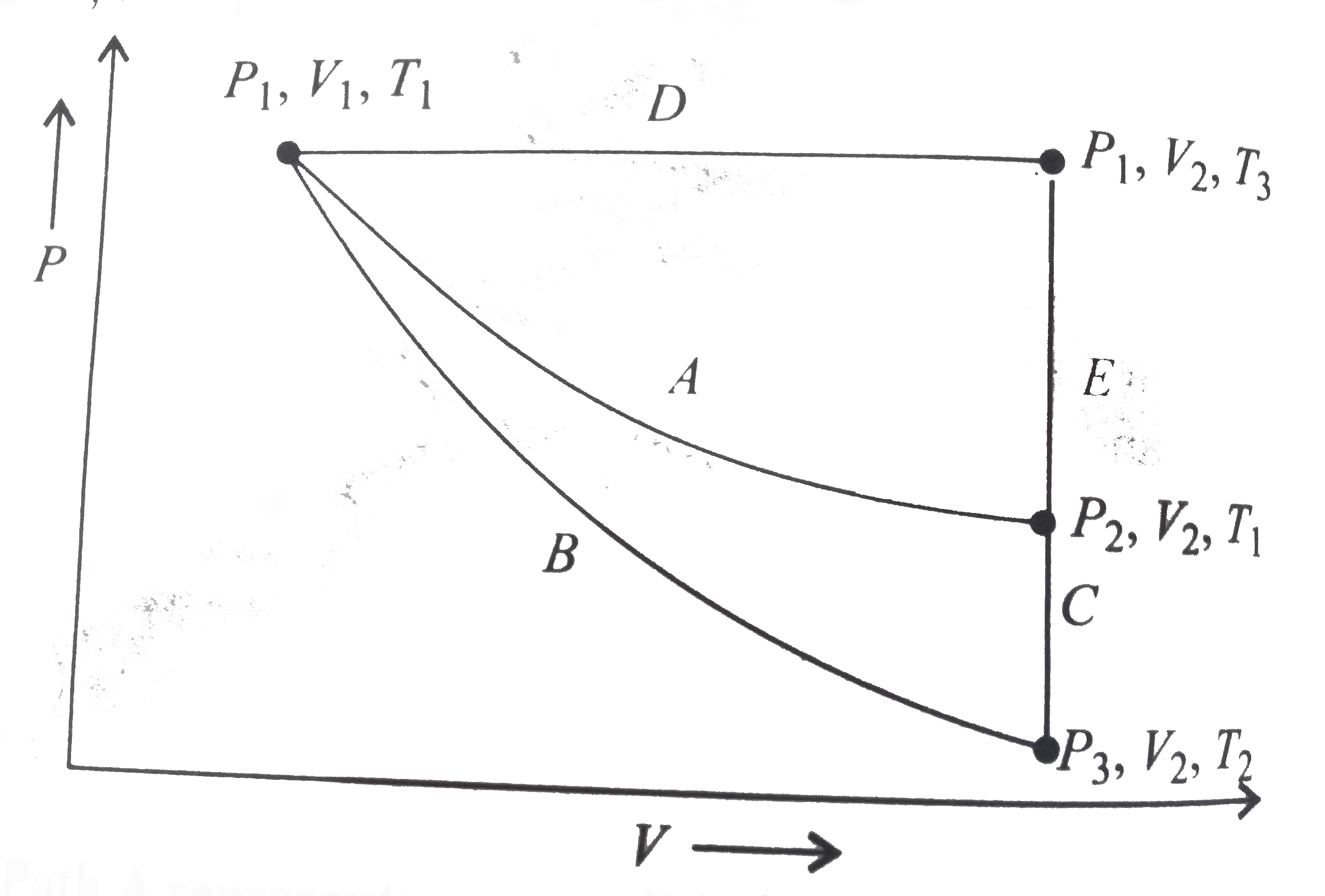
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P_(1), V_(1), T_(1) to a final state P_(2), V_(2),T_(1) is shown in the given figure. Path A represents a reversible isothermal expansion form P_(1),V_(1) to P_(2),V_(2) , Path (B+C) represents a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2) followed by reversible heating the gas at constant volume (C) from P_(3),V_(2),T_(2) to P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) to P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) from P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1) . What is q_(rev) , for path (B +C) ?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
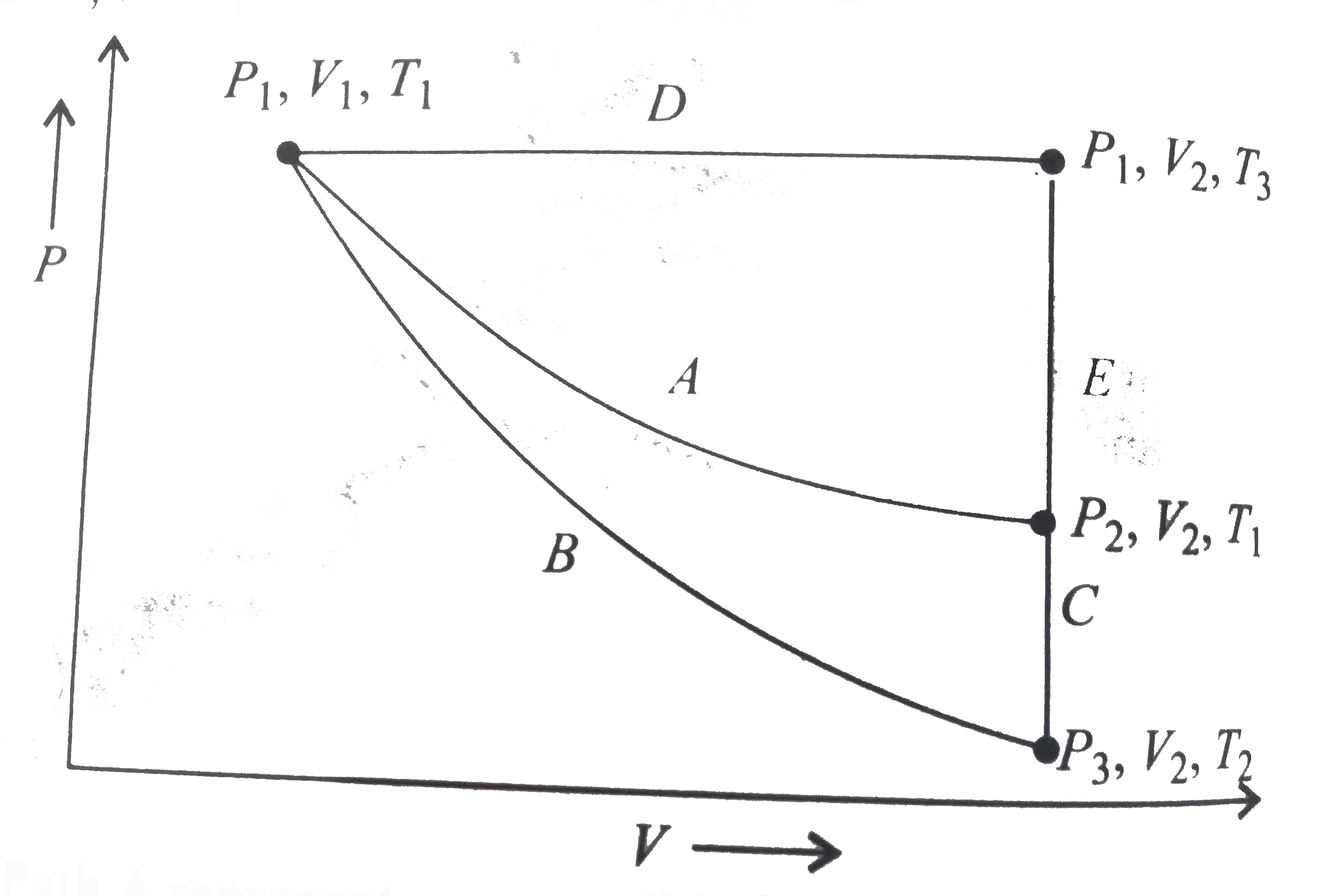
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
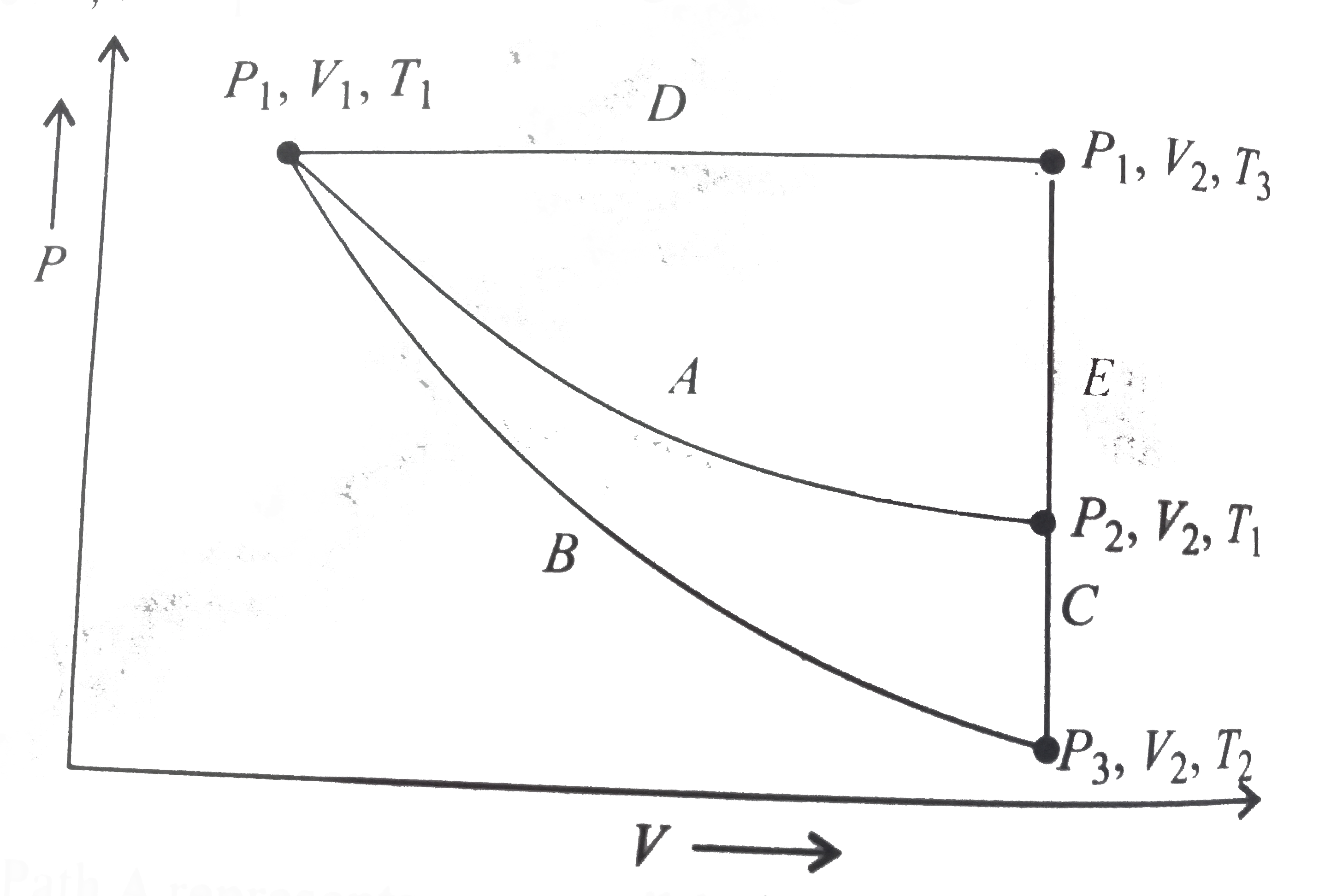
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P_(1), V_(1), T_(1) to a final state P_(2), V_(2),T_(1) is shown in the given figure. Path A represents a reversible isothermal expansion form P_(1),V_(1) to P_(2),V_(2) , Path (B+C) represents a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2) followed by reversible heating the gas at constant volume (C) from P_(3),V_(2),T_(2) to P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) to P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) from P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1) . What is DeltaS for path (D +E) ?
View SolutionAn ideal gasa undergoes through folowing cyclic procees. 1-2 : Reversible adialbatic comparession from P_(1)V_(1)T_(1)"to"P_(2)V_(2)T_(2) 2-3 : Reversible isochoric heating from P_(2)V_(2)T_(2)" to " P_(3)V_(3)T_(3) 3-4 Reversible adialbatic expansion from P_(3)V_(3)T_(3)" to " P_(4)V_(4)T_(4) 4-1 Reversible isochoric cooling from P_(4)V_(4)T_(4)" to " P_(1)V_(1)T_(1) Eefficiencyof the cycle is :
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P_(1),V_(1),T_(1) to a final state P_(2),V_(2),T_(1) is shown in the given figure . Path A represents a reversible isothermal from P_(1)V_(1)" to "P_(2),V_(2) , path (B+C) represent a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)" to " P_(3),V_(2),T_(2) followed by reversible heating of the gas at constant volume (C) from P_(3),V_(2),T_(2) " to " P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) " to "P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) form P_(1),V_(2),T_(3) " to "P_(2),V_(2),T_(1) What is q_("rev") for path (A)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P_(1),V_(1),T_(1) to a final state P_(2),V_(2),T_(1) is shown in the given figure . Path A represents a reversible isothermal from P_(1)V_(1)" to "P_(2),V_(2) , path (B+C) represent a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)" to " P_(3),V_(2),T_(2) followed by reversible heating of the gas at constant volume (C) from P_(3),V_(2),T_(2) " to " P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) " to "P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) form P_(1),V_(2),T_(3) " to "P_(2),V_(2),T_(1) What is DeltaS for path (A)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
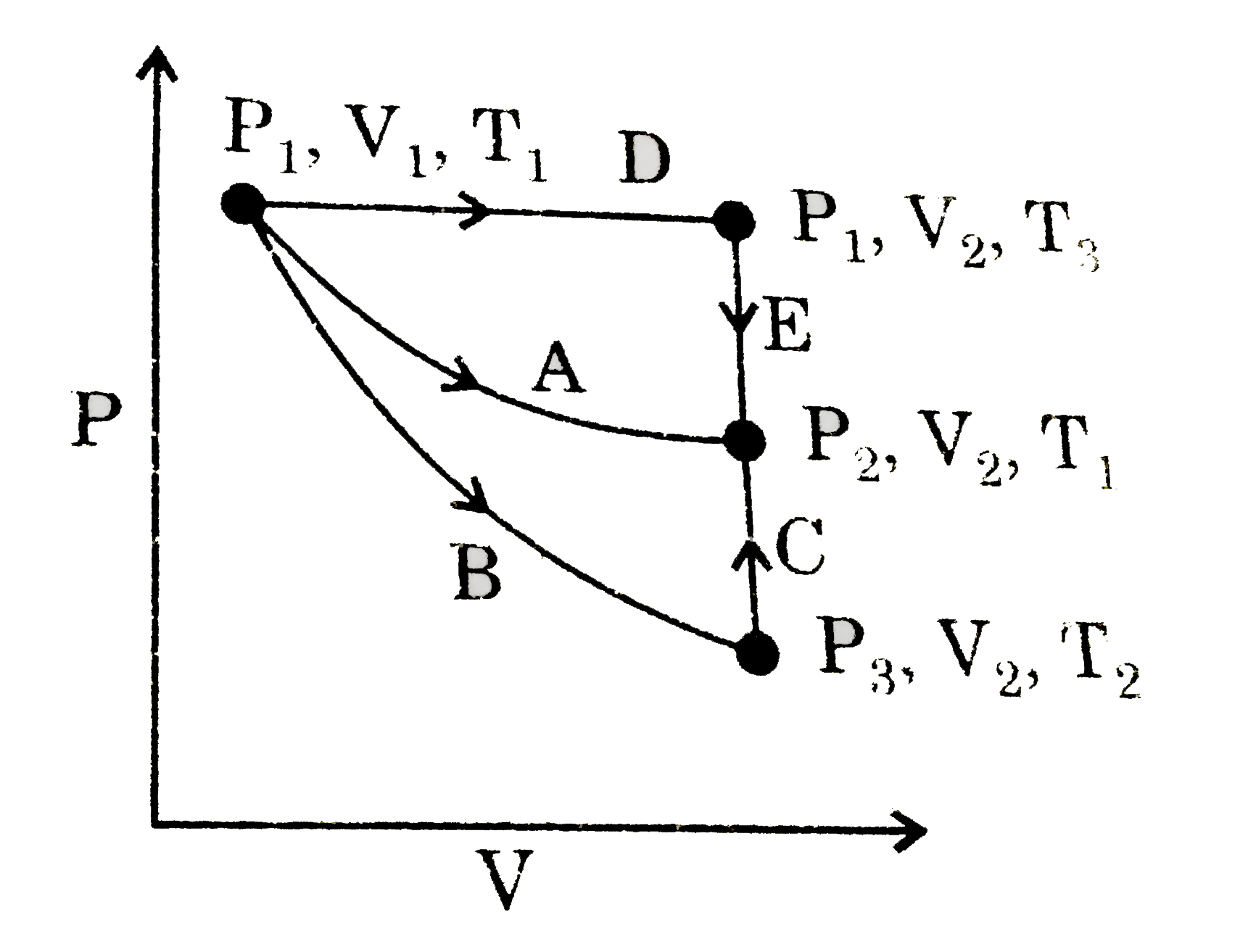
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionFor an ideal gas, an illustration of the different paths, A (B+C) and (D+E) from an intial state P1,V1,T1 to a final state P2,V2,T1 as shown in the given figure.
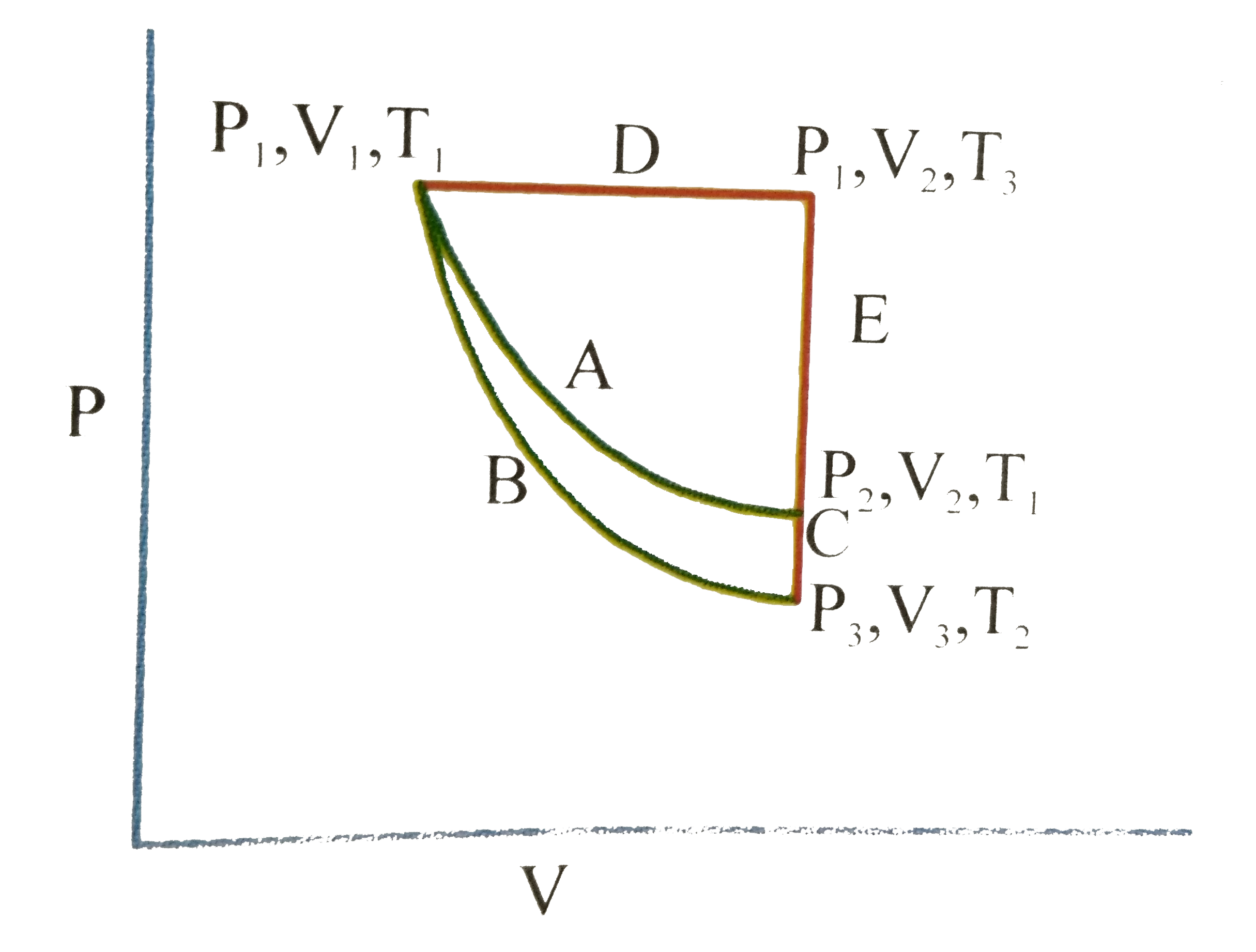
Path (A) represents a reversible isothernal expanison from P1V1 to P2V2. Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating the gas at constant volume (C) from P3,V2,T2 to P2,V2T1 to P1,V2,T3 followed by reversible cooling at a constant volume V2 (E) from P1,V2,T3 to P2,V2,T1
What is ΔS for path (D+E) ?
View SolutionEstablish gas equation, (P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2)) .
View Solution
