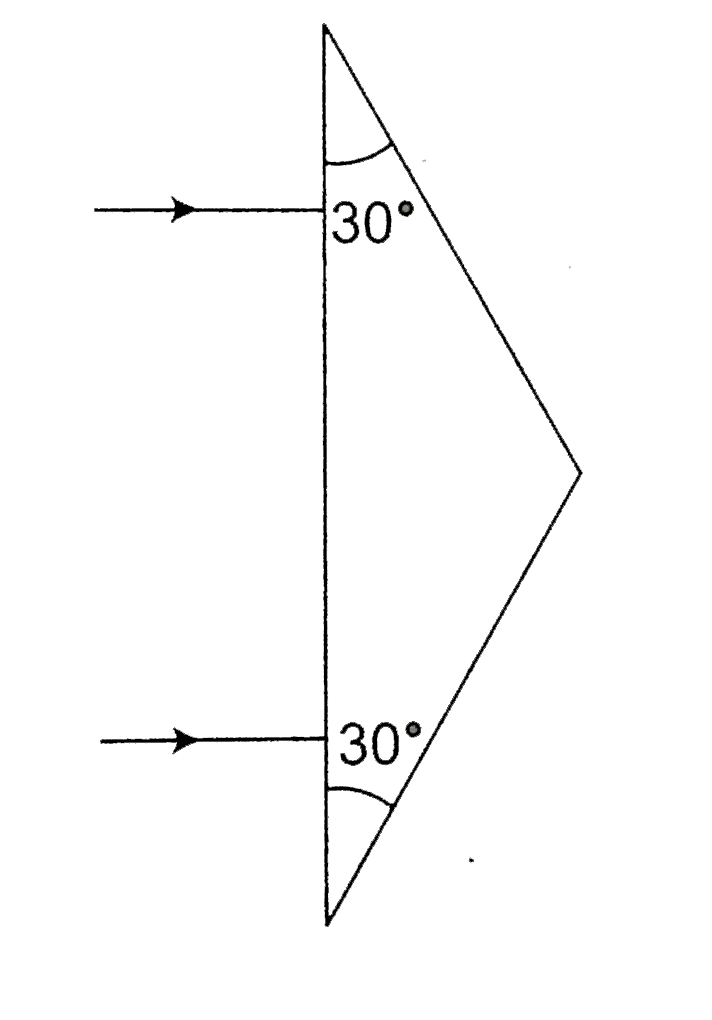
The prism shown in figure has a refractive index of 1.60 and the angles A are 30∘. Two light rays P and Q are parallel as they enter the prism. What is the angle between them after they emerge? [sin−1(0.8)=53∘]
![The prism shown in figure has a refractive index of 1.60 and the angles A are 30^@. Two light rays P and Q are parallel as they enter the prism. What is the angle between them after they emerge? [sin^-1(0.8)=53^@]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V05_C31_E01_029_Q01.png)
The correct Answer is:D
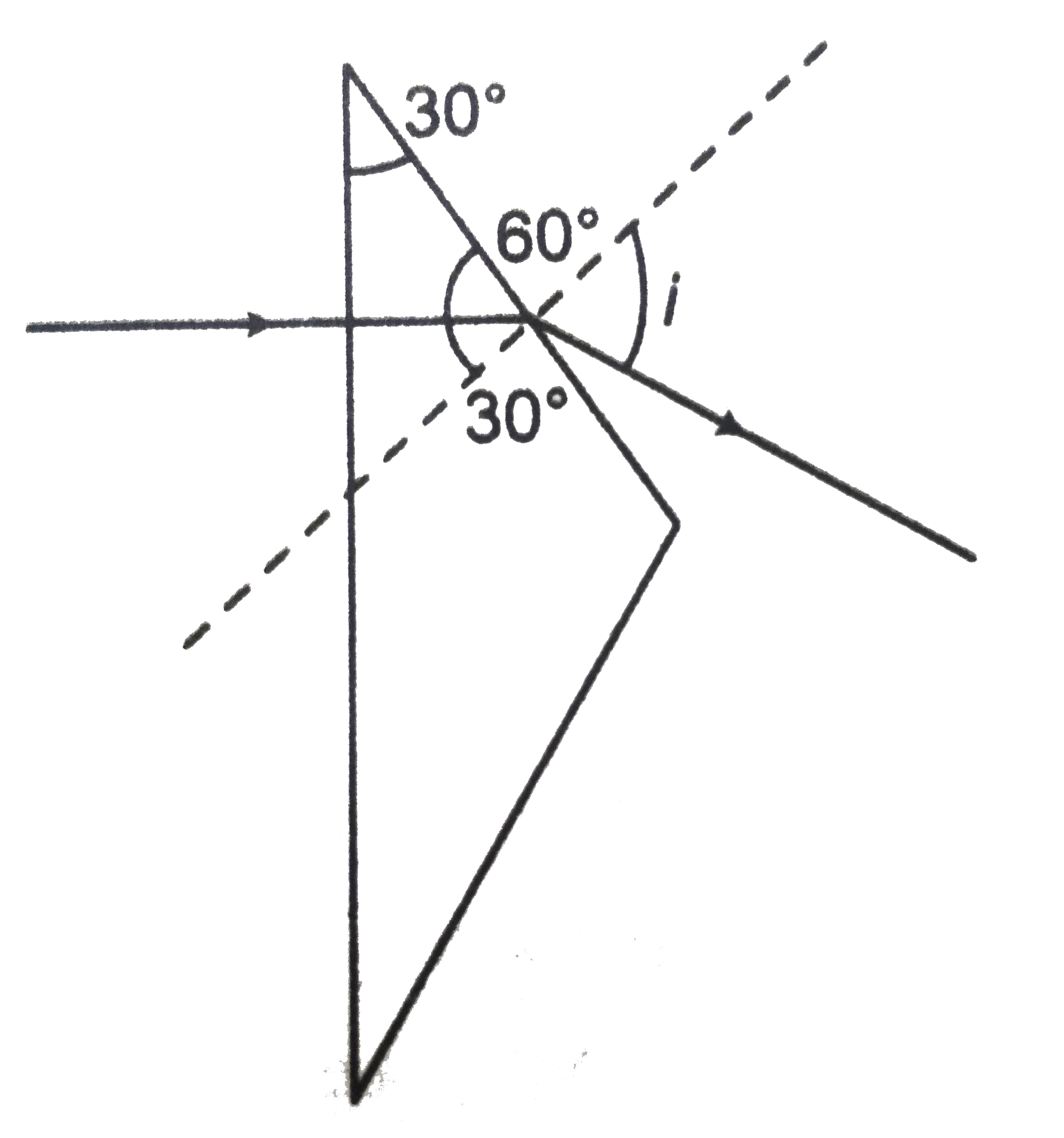
μ=sinisin30∘
∴sini=μsin30∘
=(1.6)(12)=0.8
∴i=53∘
P ray deviates from its original path by an angle,
δ=i−30∘=23∘
∴ Angle between two rays, θ=2δ
=46∘
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Objective
38 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.7
2 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
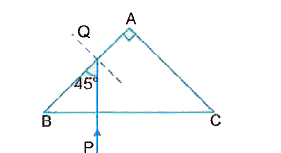
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View SolutionAn equilateral prism of unknown refractive index has a prism angle A. A light ray incident at an angle 0.8 A suffers minimum deviation. What will be the speed of light inside the prism ?
View Solution
Knowledge Check
Two parallel light rays are incident at one surface of a prism of refractive index 1.5. What is the angle between the rays as they emerge? sin−1(0.75)=48.5∘
 A19∘B37∘C45∘D30∘
A19∘B37∘C45∘D30∘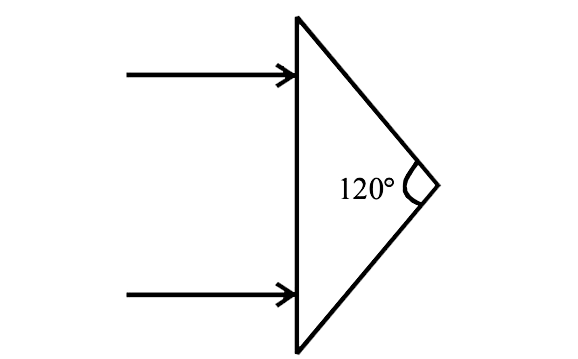
An isosceles prism of angle 120degree has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite facesAare parallel to each otherBare divergingCmake an angle 2[sin−1(0.72)−30degree] with each otherDmake an angle 2sin−1(0.72) with each otherA glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
A60∘B30∘C45∘Dthe ray does not emerge
(a) If the refracting angle of a prism is 60∘ and the minimum deviation is 30∘, then find the angle of incidence.
(b) A ray of light passes through an equilateral prism such that the angle of emergence is equal to the angle of incidence and each is equal to 3/4th of the angle of prism. Find the angle of deviation.
(c) The refracting of a prism is A and the refractive index of the material of the prism is cotA/2. Find the angle of deviation.
(d) The angle of a prism is 60∘. What is the angle of incidence for minimum deviation? The refractive index of the material of the prism is √2.
View SolutionA monochromatic ray of light strikes one face of a prism at an angle of 60∘ and the angle of refraction is 30∘ . The refracting angle of the prism is 60∘ . What is the angle of emergence ?
View SolutionThe angle of prism is 60∘ and its refractive index is 1.5. There will be no emergent light if the angle of incidence on the first face is
View SolutionRefractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. They ray emerges normally from the other face of the prism. The refractive index of the prism material is
View Solution
