(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
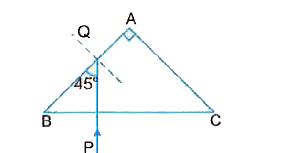
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
(a) Refraction of light rays through a prism has been shown below .
Here ∠i is the incidence angle at first surface of prism and ∠e is the angle of emergence from the second surface ∠r1and∠r2 are the respective refraction angles at the two faces and ∠δ is the angle of deviation.
Now in ΔQMR, ∠r1+∠r2+∠M=180∘ ...(i)
and in quadrilateral AQMR, ∠A+90∘+∠M+90∘=360∘
or ∠A+∠M=180∘ ...(ii)

Comparing (i) and e(ii), we get
∠r1+∠r2=∠A ...(iii)
Now in ΔJQR∠δ=∠JQR+∠JRQ
=(∠i−∠r1)(∠e−∠r2)=∠r+∠e−(∠r1+∠r2)=∠i+∠e−∠A
⇒∠i+∠e=∠A+∠δ ....(iv)
A graph showing variation in angle of deviation (δ) with variation in angle of incidence (i) is also shown below . As minimum deviation position corresponds to only one angle of incidence, it means that for minimum deviation position ∠i=∠e and also ∠r1=∠r2=r (say) .
So in minimum deviation position , we have
∴∠A=∠r1+∠r2=∠r+∠r=2∠r or ∠r=(A2)
and ∠A+∠δm=∠i+∠e=∠i+∠i=2∠i or ∠i=(A+δm2)
∴ Refractive of prism n=sinisinr=sin(A+δm2)sin(A2)
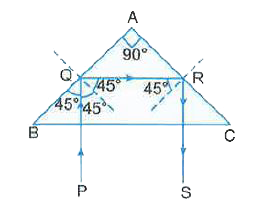
(b) (i) Complete path of the ray through the prism has been traced. Since critical angle of prism is ic=sin−1(11.5)=42∘ , the light ray undergoes total internal reflection two times as shown .
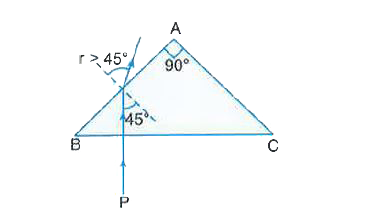
(ii) If refractive index of prism is n = 1.4 , then critical angle ic=sin−1(11.4)=45.6∘ . In that case the light ray will be refracted into air at point Q and deviates away from the normal as shown below .
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - C
7 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
11 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Draw a ray diagram showing the path of a ray of light entering through a triangular glass prism. Deduce the expression for the refractive index of glass prism in terms of the angle of minimum deviation and angle of the prism.
View SolutionDraw ray diagram showing refraction of monocromatic light through a glass prism and hence obtain the relation between refractive index (μ) of the prism and angle of minimum deviation.
View Solution
Knowledge Check
When a ray of light falls on a prism of angle 48∘ , it suffers minimum deviation. Refractive index of the material of prism is 1.6. The angle of incidence is nearly
A16∘B48∘C30∘D41∘The angle of a prism is 60∘ and its refractive index is √2 . The angle of minimum deviation suffered by a ray of light in passing through it is
AAbout 20∘B30∘C60∘D45∘A ray of light is incident at an angle of 60∘ on the face of a prism with an angle of 60∘. Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
A1.414B1.623C1.524D1.732
Plot a graph to show the variation of the angle of deviation as a function of angle of incidence for light rays passing through a prism. Write the relation for the refractive index of the prism in terms of the angle of minimum deviation and the angle of the prism.
View SolutionWhat is a prism ? Draw a neat diagram to show refraction of a light ray through a triangular glass prism. Define angle of deviation.
View SolutionA ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
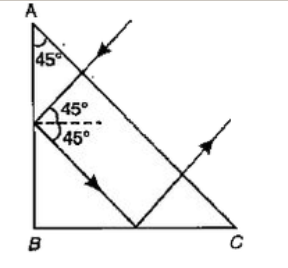
View SolutionWhile passing through a prism of angle 6∘ a ray of light undergoes a devation of 3∘. The refractive index of the material of the prism is ____________.
View SolutionA trihedral prism with refracting angle 60∘ deviates a light ray by 30∘. The refractive index of the material of prism
View Solution
