The pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
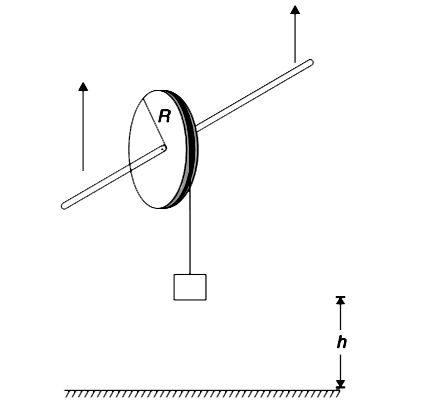
The correct Answer is:3hR
Step by step video, text & image solution for The pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
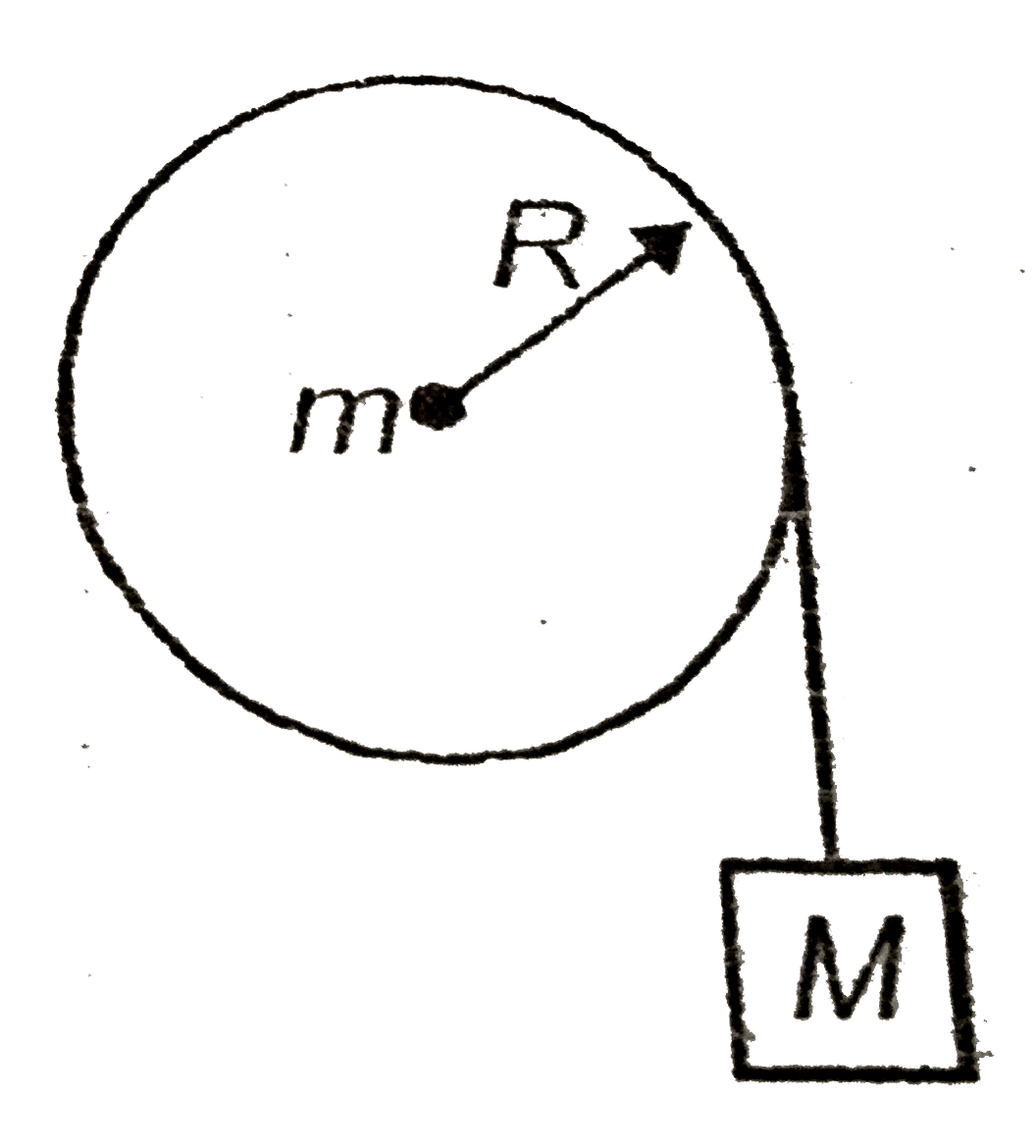
A disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
View Solution
Knowledge Check
Both the blocks shown in figure have same mass 'm'. All the pulley and strings are massiess.
AAcceleration of block A is 2g5BAcceleration of block A is g5CAcceleration of block B is g5DTension in the attached with A is 3mg5In the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is
Ag/2BgCg/3DNone of theseThe system shown in the figure consider of a light , inextenslible cord, light, frictionless pulley, and blocks of equal mass. Notice that block B is attached to one of the pulleys. The system is initial held at rest so that the ground . The blocks are then released. Find the speed of block A at the moment the vertical separation of the blocks is h.
A√6gh15B√8gh13C√8gh15D√6gh13
A disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionA solid uniform cylinder of mass M and radius R is pivoted at its centre free to rotate about horizontal axis. A massless inextensible string is wrapped around it, and attached to a block of mass m which is initially at a height h above the floor. The acceleration due to gravity is g, directed downward. The block is released from rest. By what total angle does it rotate Δθ (in radians)
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
View SolutionA metallic pulley is in the shape of a disc of radius a. It can rotate freely about a horizontal axis passing through its centre. The moment of inertia of the pulley about this axis is I. A light string is tightly wrapped around the pulley with its one end connected to a block of mass M. The centre of the pulley and its circumference are connected to a resistance R as shown. The contact of resistance at the circumference does not cause any friction. A uniform magnetic field B is switched on which is parallel to the axis of rotation of the pulley (see Figure). The mass M is allowed to fall. Assume that resistivity of the material of the pulley is negligible.
(a) Find the acceleration of the block of mass M at the instant its velocity becomes v0.
(b) Assuming that the block can fall through a large distance, calculate the terminal speed (vT) that it will acquire.
(c) Find the rate of change of kinetic energy of the pulley at the instant speed of the falling block is vT2.
View SolutionA uniform cylindrical pulley of mass M and the radius R can freely rotate about the horizontal axis O (figure). The free end of a thread tightly wound on the pulley carries a deadweight A. At a certain angle α it counterbalanes a point mass m fixed at the rim of the pulley. Find the frequency of small osicllations of the arrangement.
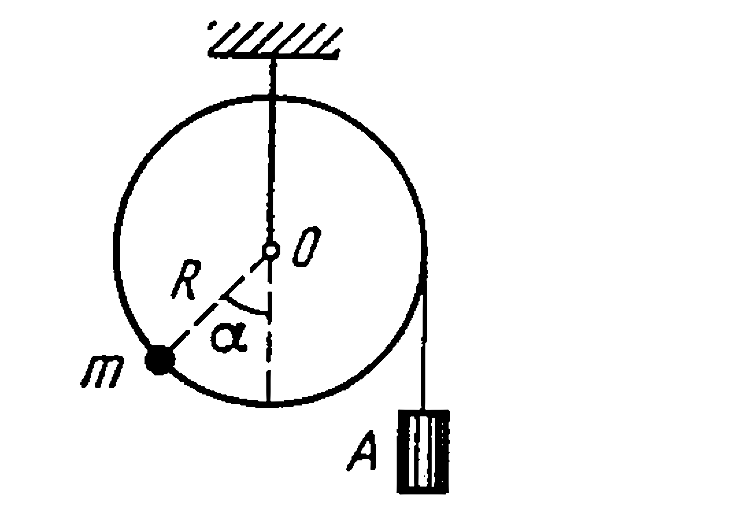
View Solution