A disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
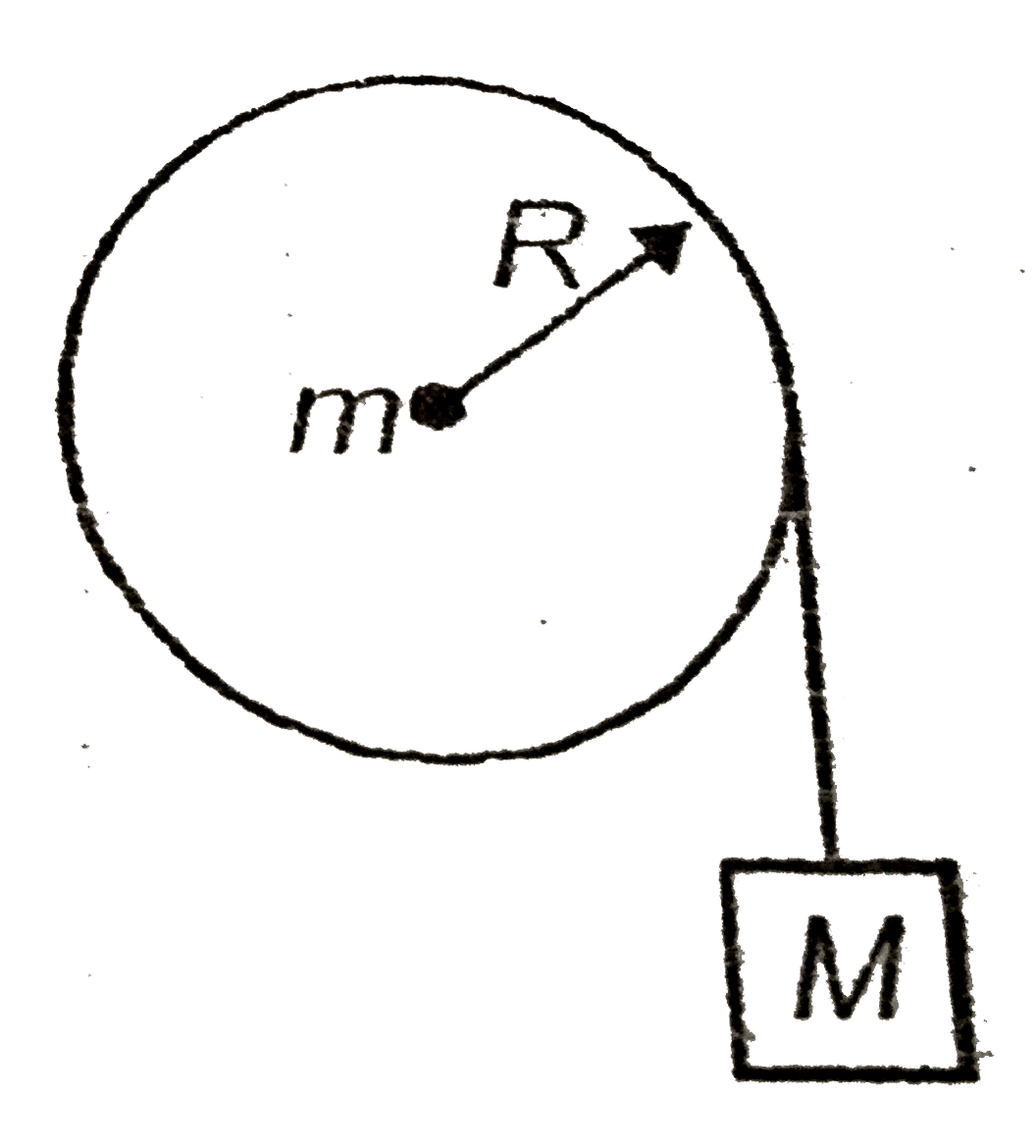
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
we choose the puley and mass as two separate systems and draw free body diagrams as shown.
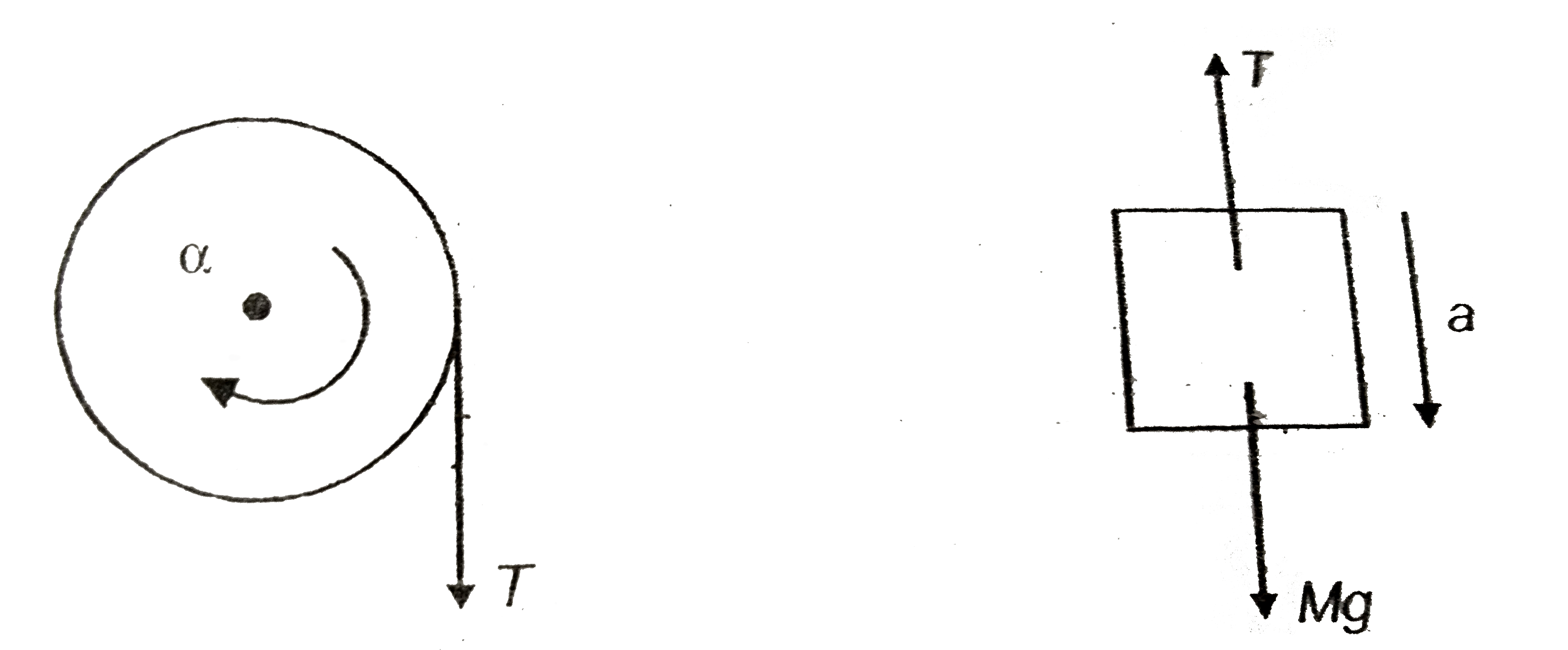
Applying Newton's Second Law in translational form,
Mg−T=Ma……..(1) [For the block]
Applying Newton's Second Law in Rotational form,
∑Tcm=lcm⋅α⇒TR=mR22α........(2) [For the disc]
If point P on the pulley rotates by any angle θ, the block of mass M moves down by a distance X, such that x=Rθ
Differentiating this equation twice we get
d2xdt2=Rd2dt2
a=Rα.........(3)
Using equations (1), (2) and (3), we get
Mg−T=Ma
and T=ma2........(4)
Adding the two equations
a=Mg(M+m2)
⇒a=202+2=5m/s2
⇒α=aR=50.5=10rad/s2
Tension T=ma2=5N [from equation (4)]
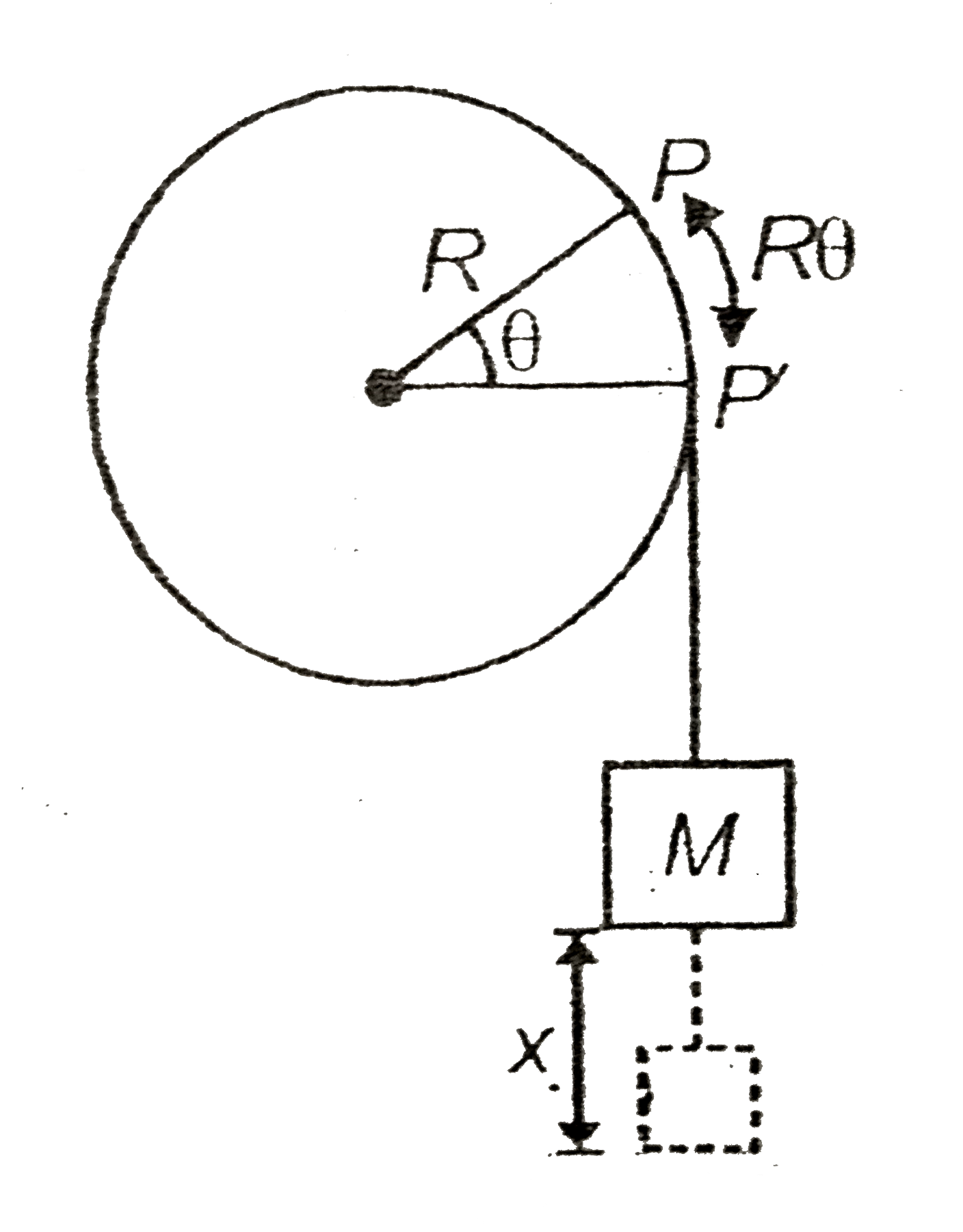
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
Two masses m1 and m2 are joined with the help of massless string passing over a pulley of Radius R and mass M. Assume that string doesn't slip over the pulley. Take m1=10kg, m2=5kg, M=10kg, R=1m.

(a) Calculate the acceleration of each book.
(b) Calculate the tensions in the thread.View Solution
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.View Solution
Knowledge Check
- Question 1 - Select One
If the string & all the pulleys are ideal, acceleration of mass m is :-
 Ag2B0CgDdependent on m
Ag2B0CgDdependent on m - Question 2 - Select One
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
Ag2Bg3Cg5Dg10 - Question 3 - Select One
A pulley fixed to the ceiling carries a string with blocks of mass m and 3m attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
A0Bg/4Cg/2D−g/2
A metallic pulley is in the shape of a disc of radius a. It can rotate freely about a horizontal axis passing through its centre. The moment of inertia of the pulley about this axis is I. A light string is tightly wrapped around the pulley with its one end connected to a block of mass M. The centre of the pulley and its circumference are connected to a resistance R as shown. The contact of resistance at the circumference does not cause any friction. A uniform magnetic field B is switched on which is parallel to the axis of rotation of the pulley (see Figure). The mass M is allowed to fall. Assume that resistivity of the material of the pulley is negligible.
(a) Find the acceleration of the block of mass M at the instant its velocity becomes v0.
(b) Assuming that the block can fall through a large distance, calculate the terminal speed (vT) that it will acquire.
(c) Find the rate of change of kinetic energy of the pulley at the instant speed of the falling block is vT2.
 View Solution
View SolutionIn the pulley system shown the movable pulleys A,B and C have mass m each, D and E are fixed pulleys. The strings are vertical light and inextensible Then
 .View Solution
.View SolutionFind the acceleration blocks in fig. The pulley and the string are massless.
 View Solution
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 View Solution
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View Solution

