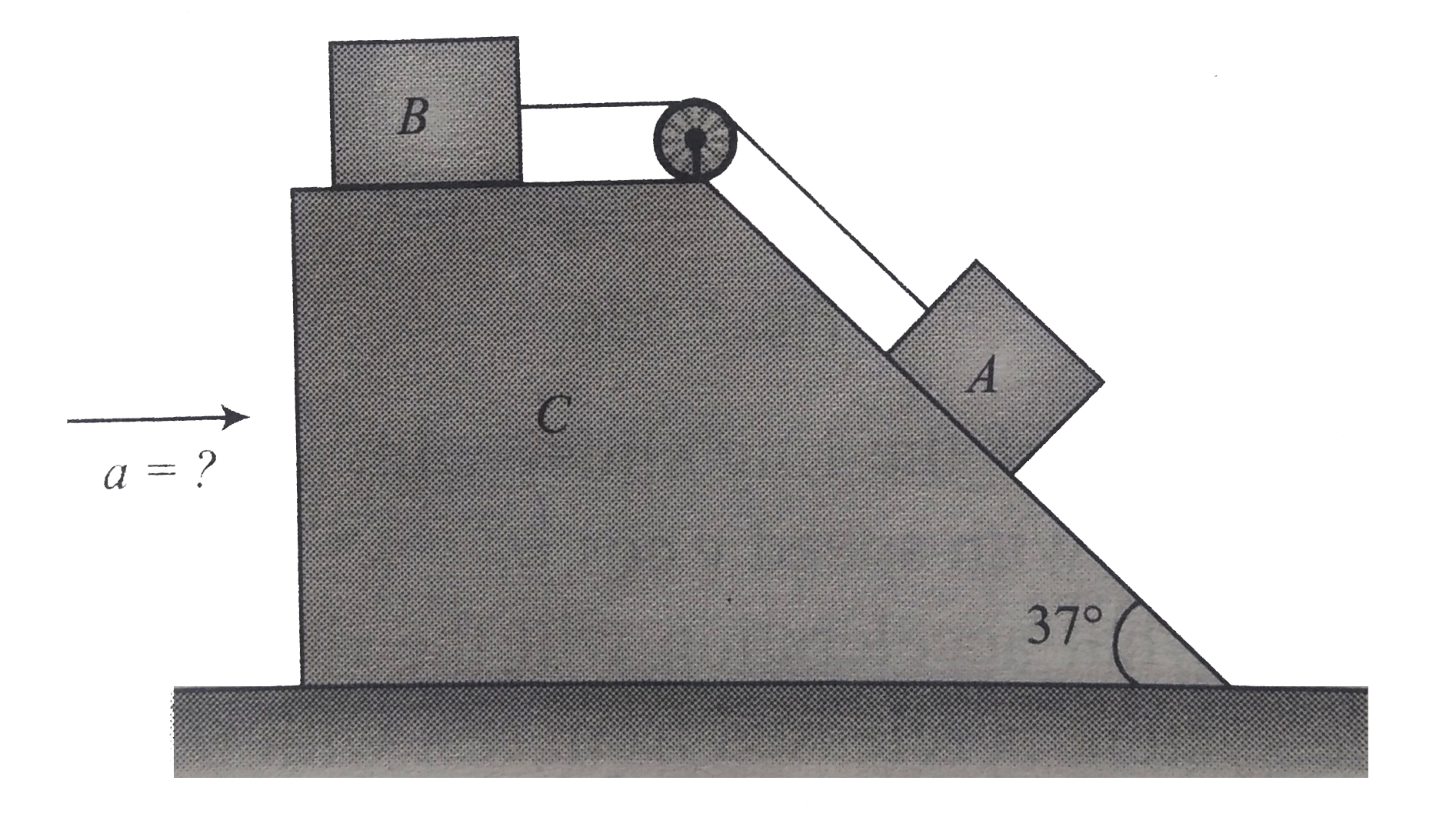
The pulley of the system shown in Fig is massless and frictionless and thread and thread is inextensible Then horizontal surface over which block $C$ is smooth while for all the remaining surface is $μ$

Calculate minimum acceleration a with which the system should be moved to the right so that suspented block $A$ (mass m ) and $B$ (mass $M$ and $M > m)$ can remain stationary relative to $C$

Video Solution

Text Solution

Verified by Experts

Since blocks $A and B$ are stationary relative to $C$ It means their acceleration will also be equal to a (rightward). Since mass $m$ of block $A$ is less than mass $M$ of block $B$ hence block $A$ has tendency to slip upward while $B$ has tendency to slip downward .
Since $A$ has to slip upward therefore on its left surface will act downward and friction on both the surface of block $B$ will act upward because it has tendency to slip downward hence , their free body diagram will be as shown in fig

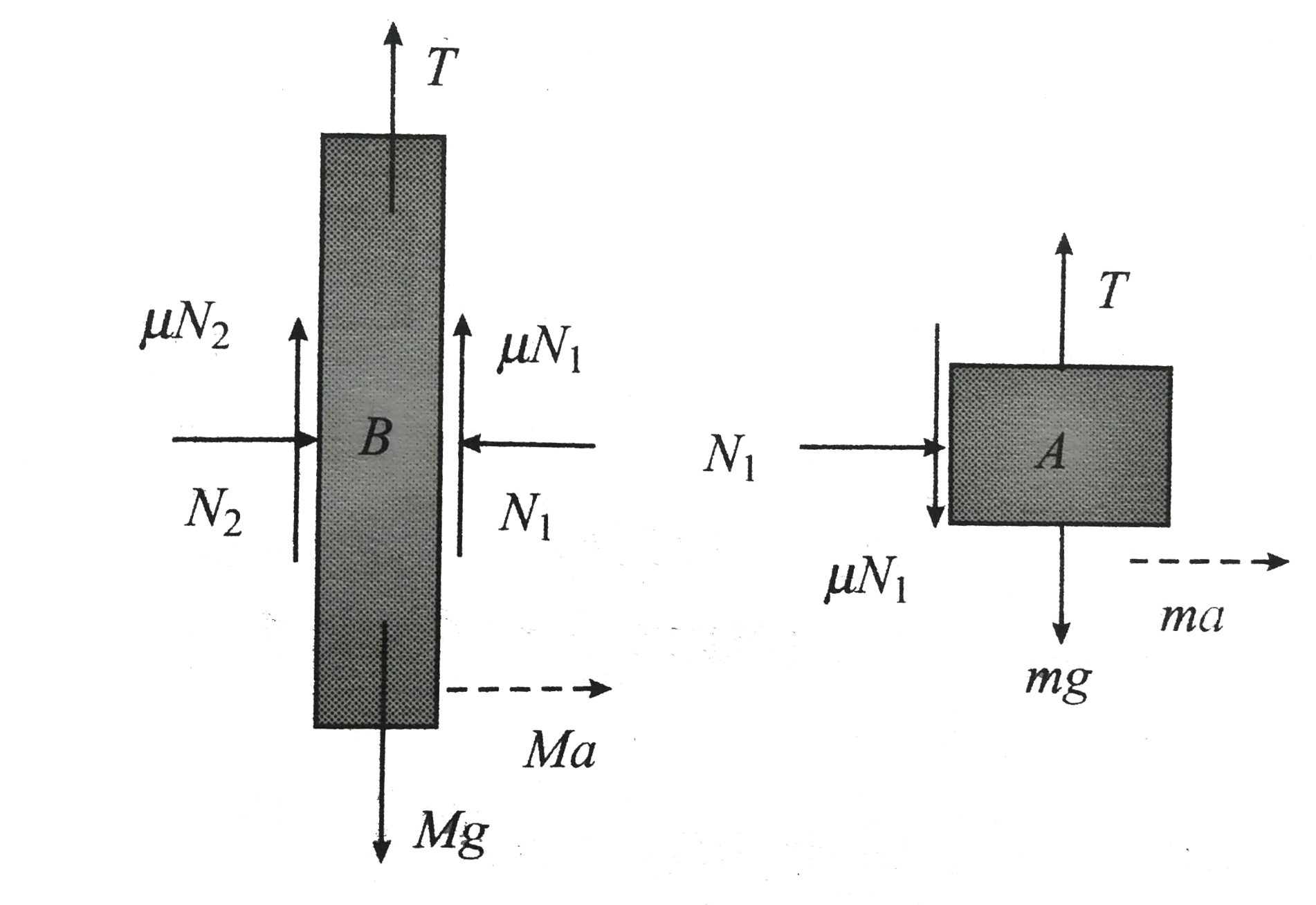
For horizontal forces on $A, N_{1} = m a$
For verticle equillibruim of $A$ ,
$T = (μ N_{1} + m g) = (μ m a + m g)$ ....(i)
For horizontal forces on $B N_{2} - N_{1} = M a$
or $N_{2} = (m + M) a$
For verticle equillibruim of $B$
$T + μ N_{1} + μ N_{2} = M g$
$(μ m a + m g) + μ m a + μ (m + M) a = M g$
$a = \frac{M - m}{μ (3 m + M)} . g$

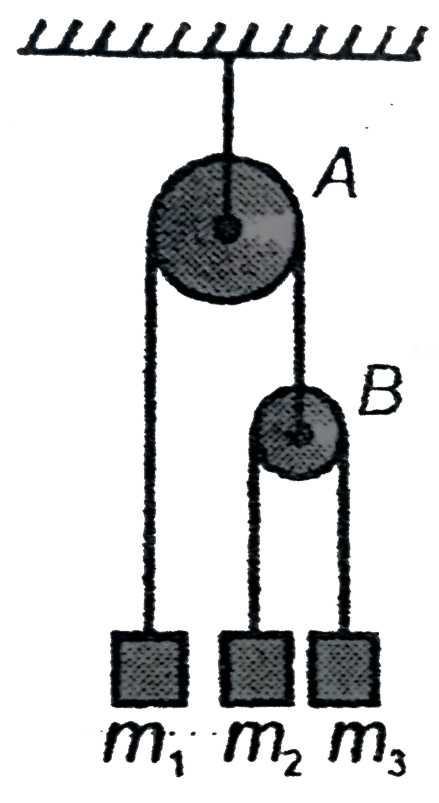
In the arrangement shown below, pulleys are mass-less and friction-less and threads are in-extensible. Block of mass $m_{1}$ will remain at rest if :

A $\frac{4}{m_{1}} = \frac{1}{m_{2}} + \frac{1}{m_{3}}$
B $m_{1} = m_{2} = m_{3}$
C $\frac{1}{m_{1}} = \frac{1}{m_{2}} + \frac{1}{m_{3}}$
D $\frac{1}{m_{2}} = \frac{2}{m_{2}} + \frac{3}{m_{1}}$
In the arrangement shown below pulleys are mass less and frictionless and threads are in responsible block of mass $m_{1}$ will remain at rest if :

A $\frac{4}{m_{1}} = \frac{1}{m_{2}} + \frac{1}{m_{3}}$
B $m_{1} = m_{2} = m_{3}$
C $\frac{1}{m_{1}} = \frac{1}{m_{2}} + \frac{1}{m_{3}}$
D $\frac{1}{m_{3}} = \frac{2}{m_{2}} + \frac{3}{m_{1}}$
Two masses $(M + m) and (M - m)$ are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
A $g m / M$
B $2 g M / m$
C $g m / 2 M$
D $g (M^{2} - m^{2}) / 2 M$