The pulse shown in figure has a speed of .

(a) If the linear mass density of the right string is 0.25 that of the left string, at what speed does the transmitted pulse travel?
(b) Compare the heights of the transmitted pulse and the reflected pulse to that of the incident pulse.
The correct Answer is:A, B, C, D
(a) Assuming tension to be same.
.
(b)
.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Assertion And Reason
10 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Objective
11 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.3
5 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
The pulse shown in Fig.7.73 has a speed of 5cm/s. If the linear mass of the right string is 0.5 that of the left string , find the ratio of height of the transmitted pulse to that of incident pulse.
View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
yi=Aicos(k1x−ω1t)
(a) What are the expressions for the transmitted and the reflected waves in terms of Ai,k1 and ω1?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionA wave pulse on a string has the dimensions shown in figure. The wave speed is v=1cm/s.
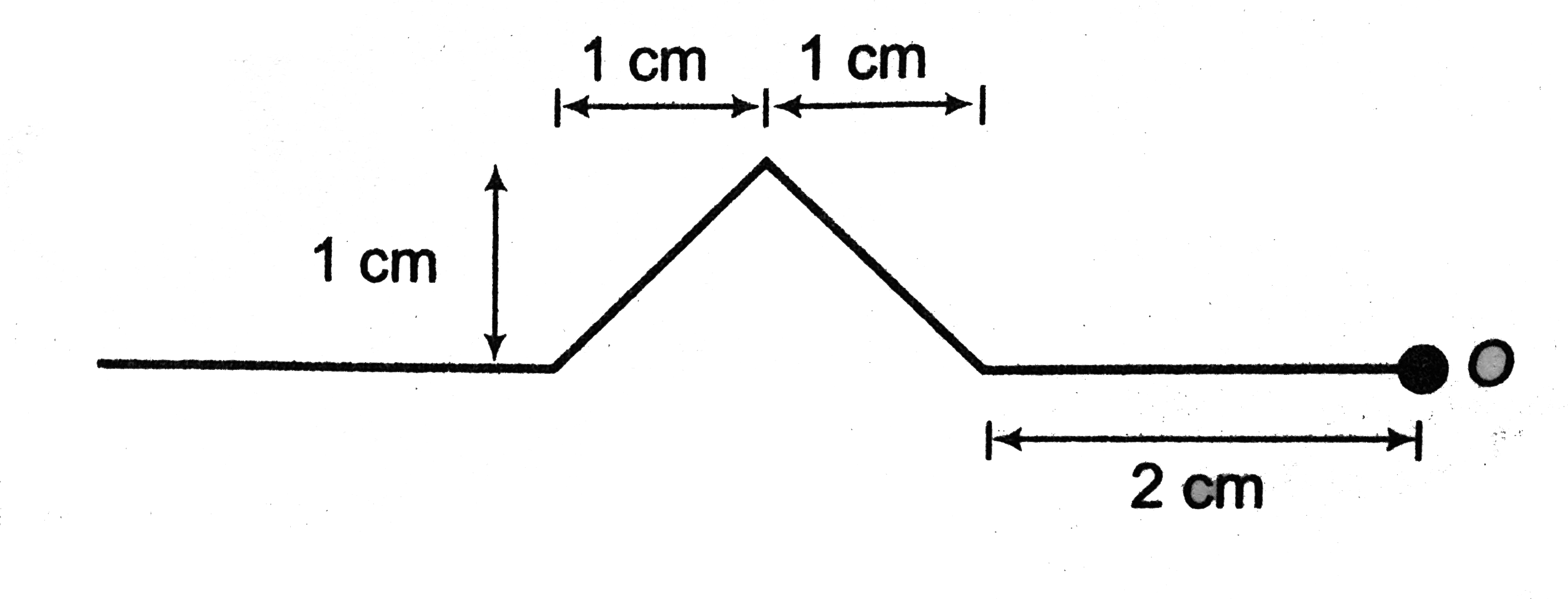
(a) If point O is a fixed end, draw the resultant wave on the string at t=3 s and t=4 s.
(b) Repeat part (a) for the case in which O is a free end.
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA pulse shown here is reflected from the rigid wall A and then from free end B. The shape of the string after these 2 reflection will be
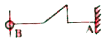
View SolutionA long wire PQR is made by joining two wires PQ and QR of equal radii. PQ has length 4.8m and mass 0.06kg. QR has length 2.56m and mass 0.2kg. The wire PQR is under a tension of 80N. A sinusoidal wave-pulse of amplitude 3.5cm is sent along the wire PQ from end P. No power is dissipated during the propagation of the wave-pulse. Calculate,
(a) the time taken by the wave-pulse to reach the other end R of the wire, and
(b) the amplitude of the reflected and transmitted wave-pulse after the incident wave-pulse crosses the joint Q.
View SolutionThe speed of sound in water is 1500 m/s. A boat man hears an echo 3 s after sending a sound pulse into the sea. What is the depth of the sea?
View SolutionA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
the shape of the string is drawn at t=0 and lthe area of the pulse elclosed by the string and the x−string is measured. It will be equal to
View Solution
