The radius of our galaxy is about 3×1020m.With what speed should a person travel so that he can reach from the centre of the galaxy to its edge in 20 years of his lifetime ?
To solve the problem of determining the speed at which a person must travel to reach the edge of the galaxy from its center in 20 years of their own lifetime, we can follow these steps:
1. Understand the Problem:
- The radius of the galaxy is given as R=3×1020 m.
- The time experienced by the traveler is t0=20 years.
2. Convert Time to Seconds:
- We need to convert the time from years to seconds for our calculations.
- t0=20 years=20×365×24×60×60
- t0=20×365×24×60×60=6.312×108 seconds.
3. Relate Distance, Speed, and Time:
- The distance the person travels (the radius of the galaxy) can be expressed as:
R=V⋅t0
where V is the speed of the traveler.
4. Apply the Concept of Length Contraction:
- According to the theory of relativity, the actual distance R as seen by an observer moving at speed V is given by:
R=R0√1−V2c2
where R0 is the proper length (the radius of the galaxy), and c is the speed of light.
5. Set Up the Equation:
- We can equate the two expressions for R:
V⋅t0=R0√1−V2c2
Substituting R0=3×1020 m and t0=6.312×108 s, we have:
V⋅(6.312×108)=3×1020√1−V2c2
6. Square Both Sides:
- To eliminate the square root, we square both sides:
(V⋅6.312×108)2=(3×1020)2(1−V2c2)
7. Expand and Rearrange:
- Expanding both sides gives:
V2⋅(6.312×108)2=9×1040−9×1040V2c2
- Rearranging gives:
V2((6.312×108)2+9×10401c2)=9×1040
8. Solve for V2:
- Isolating V2:
V2=9×1040(6.312×108)2+9×10401c2
9. Calculate V:
- Finally, calculate V using the known value of c (approximately 3×108 m/s):
V≈0.9999996c
Final Answer:
The speed V at which the person should travel is approximately 0.9999996 times the speed of light c.
- The radius of the galaxy is given as R=3×1020 m.
- The time experienced by the traveler is t0=20 years.
- We need to convert the time from years to seconds for our calculations.
- t0=20 years=20×365×24×60×60
- t0=20×365×24×60×60=6.312×108 seconds.
- The distance the person travels (the radius of the galaxy) can be expressed as:
R=V⋅t0
where V is the speed of the traveler.
- According to the theory of relativity, the actual distance R as seen by an observer moving at speed V is given by:
R=R0√1−V2c2
where R0 is the proper length (the radius of the galaxy), and c is the speed of light.
- We can equate the two expressions for R:
V⋅t0=R0√1−V2c2
Substituting R0=3×1020 m and t0=6.312×108 s, we have:
V⋅(6.312×108)=3×1020√1−V2c2
- To eliminate the square root, we square both sides:
(V⋅6.312×108)2=(3×1020)2(1−V2c2)
- Expanding both sides gives:
V2⋅(6.312×108)2=9×1040−9×1040V2c2
- Rearranging gives:
V2((6.312×108)2+9×10401c2)=9×1040
- Isolating V2:
V2=9×1040(6.312×108)2+9×10401c2
- Finally, calculate V using the known value of c (approximately 3×108 m/s):
V≈0.9999996c
The speed V at which the person should travel is approximately 0.9999996 times the speed of light c.
Topper's Solved these Questions
- THE SPECIAL THEORY OF RELATIVITYBook:HC VERMA ENGLISHChapter:THE SPECIAL THEORY OF RELATIVITYExercise:Objective
Explore 2 Videos
- THE SPECIAL THEORY OF RELATIVITYBook:HC VERMA ENGLISHChapter:THE SPECIAL THEORY OF RELATIVITYExercise:Objective 2
Explore 1 Video
- THE SPECIAL THEORY OF RELATIVITYBook:HC VERMA ENGLISHChapter:THE SPECIAL THEORY OF RELATIVITYExercise:Short answer
Explore 2 Videos
- THE NUCLEOUSBook:HC VERMA ENGLISHChapter:THE NUCLEOUSExercise:Short answer
Explore 12 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBook:HC VERMA ENGLISHChapter:THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTExercise:Short Question
Explore 9 Videos
Similar Questions
A person can see things clearly upto 3m what is the power of lens he should use so that he can see upto 12 m ?
View SolutionThe distance of a galaxy from the earth is 5.6×1025 m. Assuming the speed of light to be 3×108 m s−1 find the time taken by light to travel this distance.
View Solution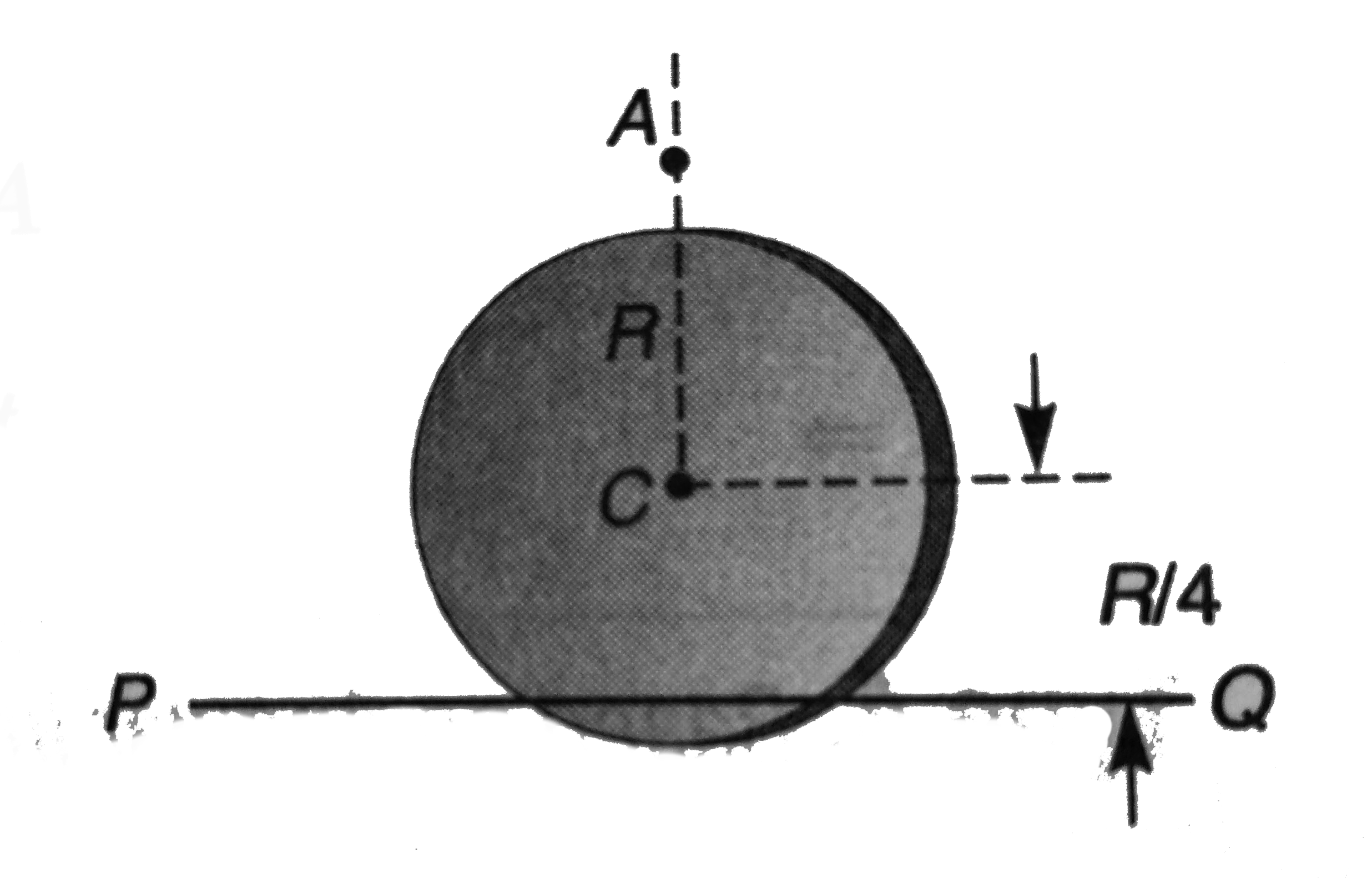
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionA swimmer S is in the sea at a distance d km from the closest point A on a straight shore The house of the swimmer is at a distance Lkm from A on the shore. He can swim at a speed of ukm/hr and walk at a speed of vkm/hr(v>u). At what point on the shore should he land so that he reaches his house in the shortest possible time?
View SolutionA stress of 106N/m2 is required for breaking a material. If the density of the material is 3×103Kg/m3, then what should be the minimum length of the wire made of the same material so that it breaks by its own weight (g=10m/s2)
View SolutionDistance between the centres of two rings is a. The masses of these rings are M and 4M. A body of mass m is fired straight from the centre of the heavier ring. What should be its minimum initial speed to cross of lighter ring ? The radius of the both ring is R. (Assume a>>R).

View SolutionWater at 20∘ is flowing in a pipe of radius 20.0cm . The viscosity of water at 20∘C is 1.005 centipise. If the water's speed in the centre of the pipe is 3.00m/s, what is water's speed:
(a) 10.0cm from the centre of the pipe(half way between the centre and the walls)
(b) at the wall of the pipe?
View SolutionA particle is travelling in a circular path of radius 4m. At a certain instant the particle is moving at 20m/s and its acceleration is at an angle of 37∘ from the direction to the centre of the circle as seen from the particle
(i) At what rate is the speed of the particle increasing?
(ii) What is the magnitude of the acceleration?
View SolutionLet us consider that our galaxy consists of 2.5×1011 stars each of one solar mass. How long will this star at a distance of 50,000 light year from the galastic entre take to complete one revolution? Take the diameter of the Milky way to be 105ly.G=6.67×10−11Nm2Kg−2.(1ly=9.46×1015m)
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular speed 100s−1. The radius of the cylinder is 0.25m. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
View Solution