The reading of an ammeter in the circuit
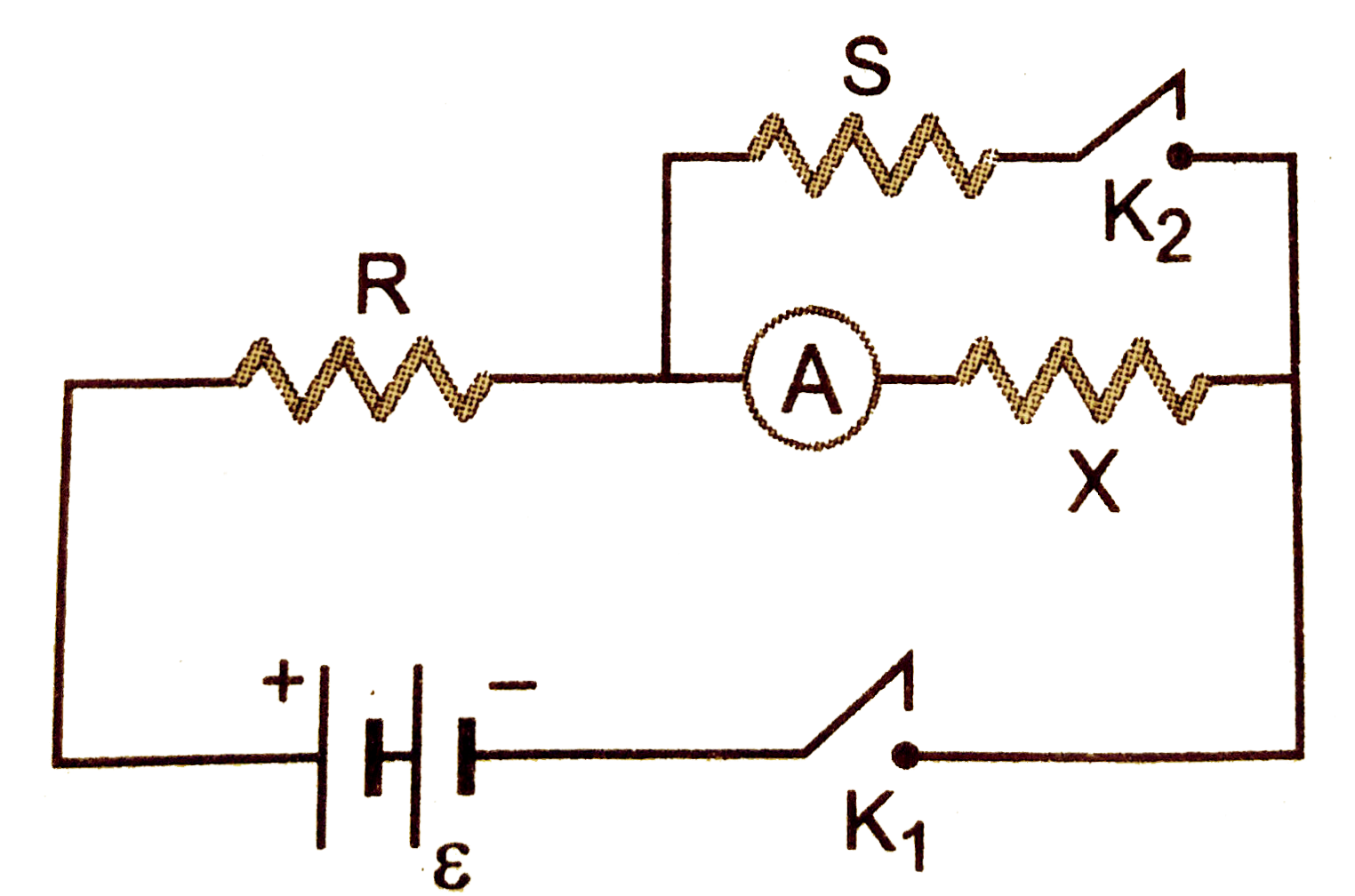
(i) I when key K1 closed key K2 is open
(ii) I/2 when both keys K1andK2 are closed Find the expression for the resistance of X in terms of the resistances of R and S
The correct Answer is:RSR−S
When key K1 is closed and K2 is open resistance of the circuit =R+X. So current
I1=IεR+X …..(i)
When key K1 is closed and K2 both are closed SandX will be in parallel then their effective resistance is
R'=SXS+X
Total resistance of circuit =R+R'=R+SXS+X
Total current I2=εR+SXS+X
Current through resistance X will be
I'2=I2×SS+X=εR+SXS+X×S(R+X)
=εS(S+X)R+SX.......(ii)
As I'2=I2
so I2=εS(S+R)R+SX [from (i) and (ii)]
or ε(R+X)2=εS(S+X)R+SX
On similarlly X=RSR−S
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)4videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-29videos
COMMUNICATION SYSTEMS
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
The reading of an ideal ammeter, in the circuit shown here, equals (i) I when key K1 is closed but key K2 is open , (ii) I2 when both keys K1 and K2 are closed. Find the expression for the resistance of X in terms of the resistance R and S.
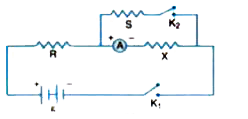 View Solution
View SolutionIn the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
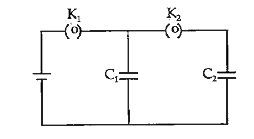 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Initially K1 is closed, now if K2 is also closed, find heat dissipated in the resistances of connecting wires
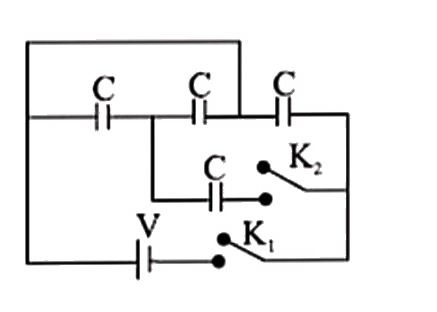 A12CV2B23CV2C13CV2D14CV2
A12CV2B23CV2C13CV2D14CV2 - Question 2 - Select One
Shown in the figure is an R−L circuit. Just after the key (K) is closed
 Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit - Question 3 - Select One

In the given ciruit Ammeter reading is same when both switches S1,S2 are closed or opened. The value of resistance R isA200ΩB100ΩC400ΩD−300Ω

The battery is charged from full wave rectifier fed by a sinuoidal voltage (see figure). Idea diodes, ammeter and voltmeter show the time average value. At idle with only key K1 closed, coltmeter shows 12 V, and current is then absent, ie, reading of ameter is 0. if only the key K2 is closed, the voltmeter shows battery voltage at 12.3 V. during charging when the K1 and K2 are closed, the voltmeter shows 12.8 V and ammeter shows 5 A. Find the internal resistance of battery.View SolutionShown in the figure is a parallel R , L,C circuit with key K1 closed and K2 opened . When K1 is opened and K2 is closed simultaneously find the maximum potential difference across the capacitor and maximum charge stored in it .
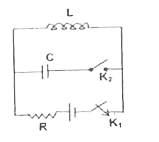 View Solution
View Solutionthe galvameter deflection , when key K1 is clossed but K2 is open equals θ0 (see figure ) On clossing k2 also and adjusting R2 to 5Ω , the deflection in galvanometer becomes θ05 the resistnce of the galvanometer is then , given by [Neglect the internal resistance of battery]:
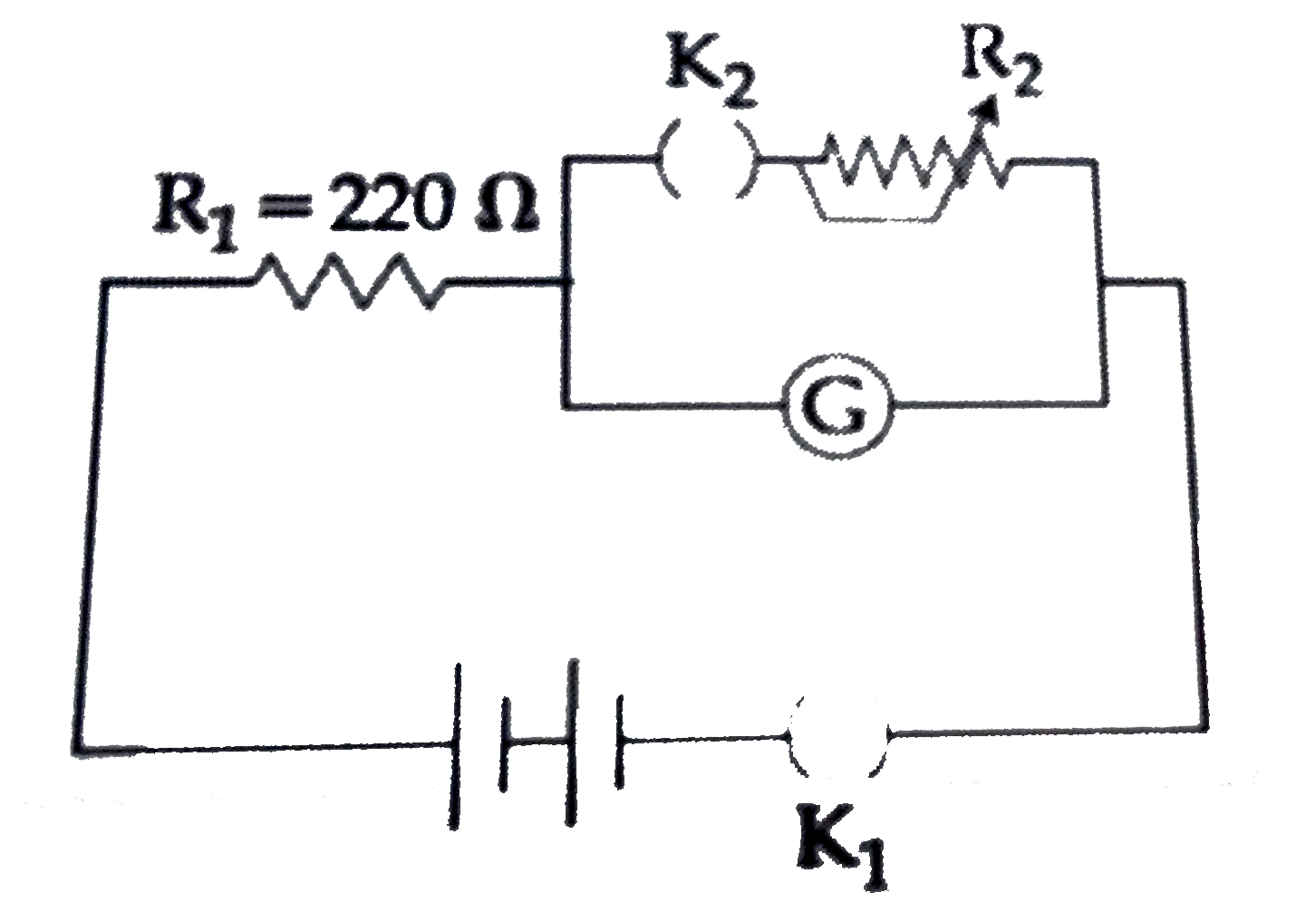 View Solution
View SolutionInitially K1 is closed, now if K2 is also closed, find heat dissipated in the resistances of connecting wires
 View Solution
View SolutionIn the circuit shown, keys K1 and K2 both are closed the ammeter reads I0. But when K1is open and K2 is closed, the ammeter reads I0/2. Assuming that ammeter resistance is much less than R2, the values of r and R1 is Omega are
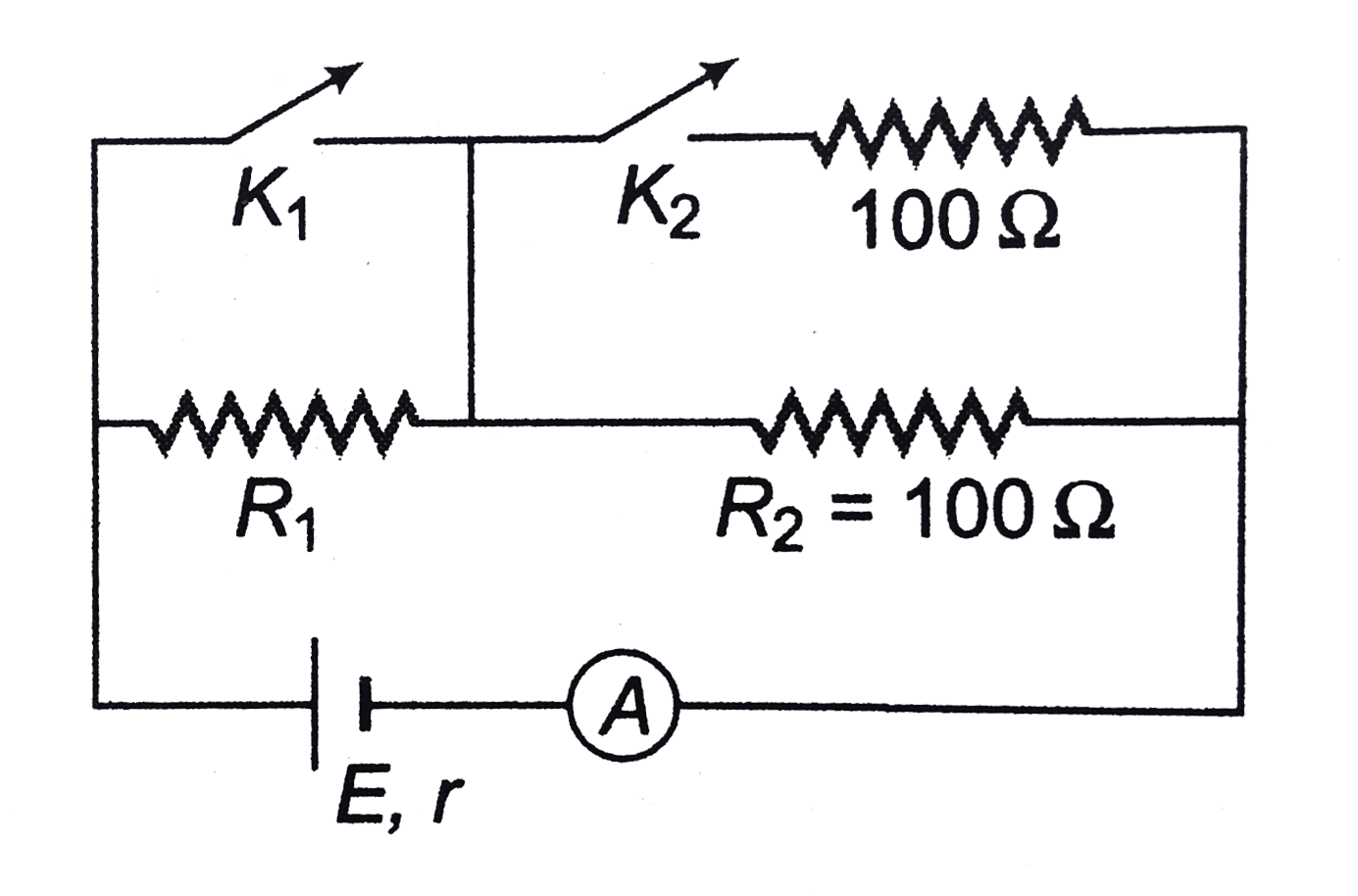 View Solution
View Solution

