The reading of an ideal ammeter, in the circuit shown here, equals (i) I when key K1 is closed but key K2 is open , (ii) I2 when both keys K1 and K2 are closed. Find the expression for the resistance of X in terms of the resistance R and S.
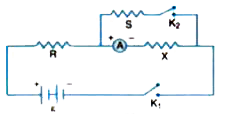
We know that resistance of an ideal ammeter is zero.
(i) When only key K1 is closed, the current flowing through the ammeter is given as :
I=εR+X ...(i)
(ii) When key K2 is also closed, the circuit current becomes
I.=εR+SXS+X
and the current flowing through the ammeter is given as :
I2=SS+X.I.=(SS+X).εR+SXS+X=Sε(S+X)R+SX ...(ii)
Multiplying (ii) by 2 and then equating with (i), we get
εR+X=2Sε(S+X)R+SX
⇒(S+X)R+SX=2S(R+X) or SR+XR+SX=2SR+2SX
⇒XR−SX=SR or X=RS(R−S)
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS - II
8 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION A (MULTIPLE CHOICE QUESTIONS))
6 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS
42 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - SELF ASSESSMENT TEST SECTION-C (VERY SHORT ANSWER QUESTIONS)
3 Videos
Similar Questions
The reading of an ammeter in the circuit
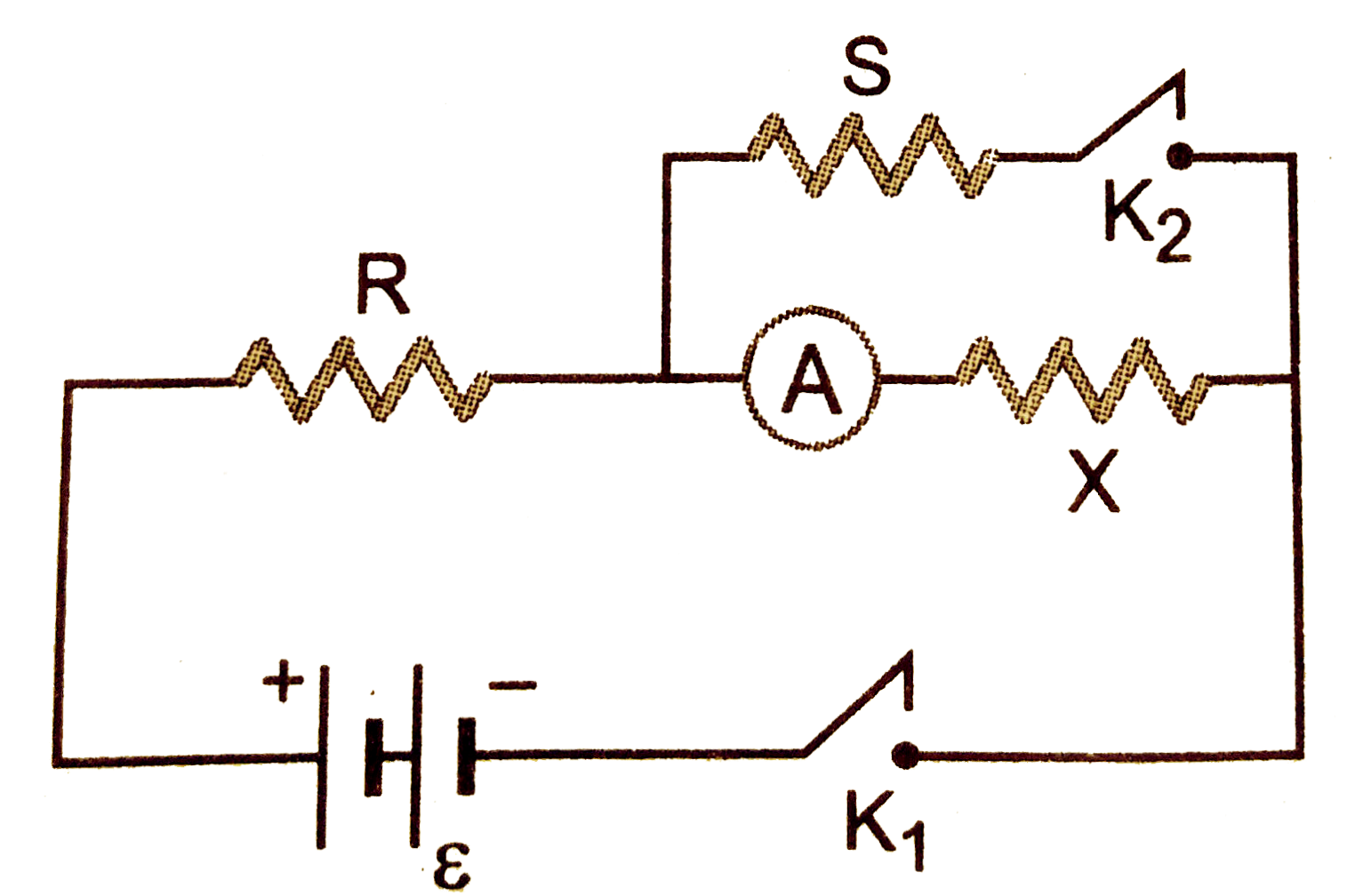
(i) I when key K1 closed key K2 is open
(ii) I/2 when both keys K1andK2 are closed Find the expression for the resistance of X in terms of the resistances of R and S
View SolutionThe reading of an ammeter in the circuit

(i) I when key K1 closed key K2 is open
(ii) I/2 when both keys K1andK2 are closed Find the expression for the resistance of X in terms of the resistances of R and S
View Solution
Knowledge Check
Shown in the figure is an R−L circuit. Just after the key (K) is closed
 Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
Athe current in the circuit is zeroBpotential drop across the resistor is zeroCemf developed across the inductor equals the emf of the batteryDno heat is dissipated in the circuit
In the circuit shown in Figure, initially key K1 is closed and key K2 is open. Then K1 is opened and K2 is closed. Then
View SolutionFor the given circuit. Calculate reading of ammeter when key K is closed.
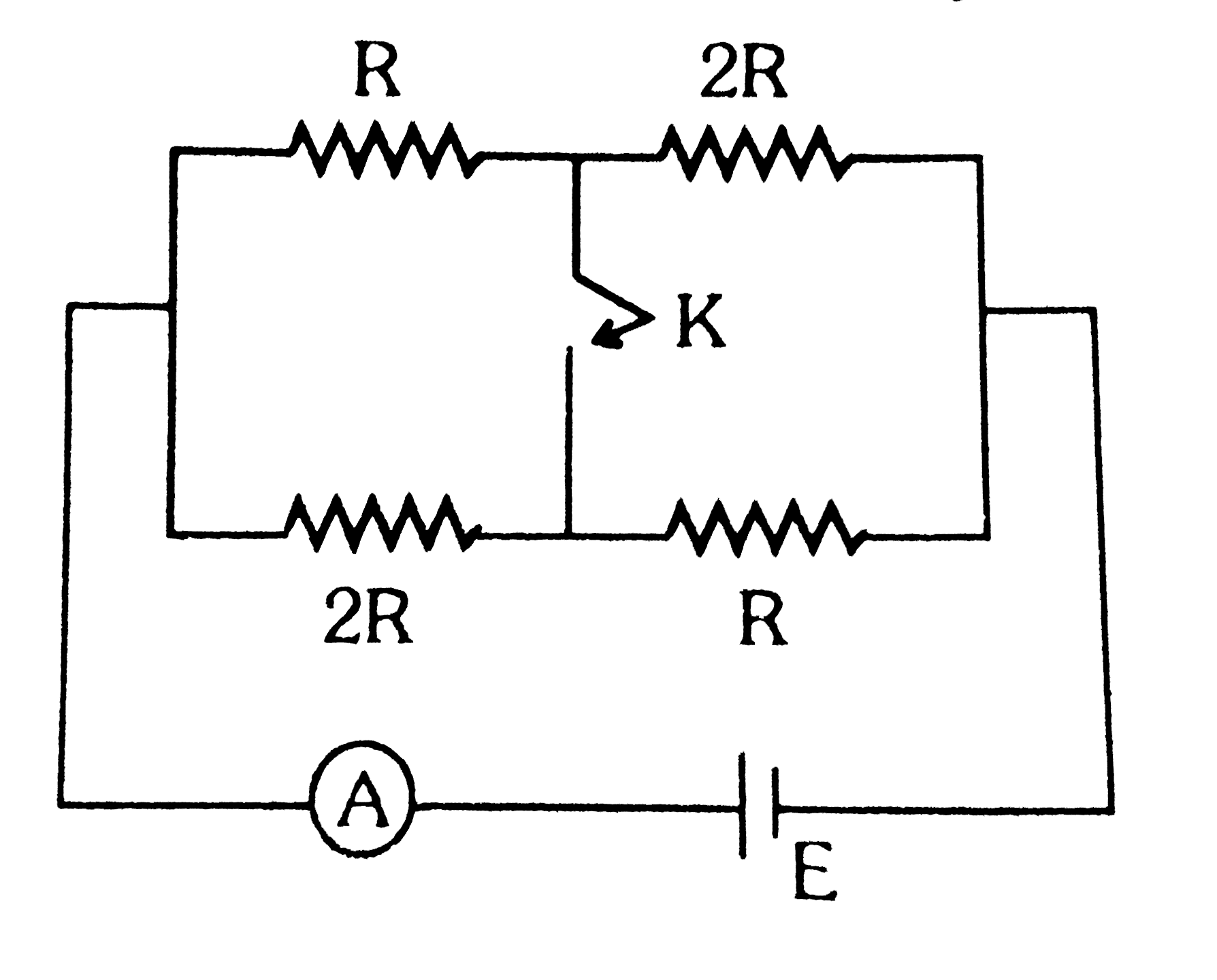
View SolutionFor the given circuit. Calculate reading of ammeter when key K is closed.

View SolutionShown in the figure is an R−L circuit. Just after the key (K) is closed

View Solution
Calculate the reading of A when
(i) K is closed.
(ii) K is open.
View SolutionIn the circuit shown in the figure, reading of ammeter is I1 when only S1 is closed, reading of of ammeter is is I2 when only S2 is closed and reading of Ammeter,is I3 when both S1 and S2 are closed then
_PHY_E05_114_Q01.png) .
.
View SolutionIn the circuit shown in the figure, reading of ammeter is I1 when only S1 is closed, reading of of ammeter is is I2 when only S2 is closed and reading of Ammeter,is I3 when both S1 and S2 are closed then
_PHY_E05_114_Q01.png) .
.
View Solution
