The refractive index μ of a medium is found to vary with wavelength λ as μ=A+Bλ2. What are the dimensions of A and B?
mu = velocity of light in vacuumvelocity of light in medium
=dimensionless number
Aμ=A+Bλ2,∴, A must be
dimensionless, and B=μλ2=[L2]
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Conceptual Problem
65 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - NCERT Exercises
40 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
When white light travels through glass, the refractive index of glass (μ=velocity of light in air/velocity of light in glass) is found to vary with wavelength as μ=A+Bλ2. Using the principle of homogeneity of dimensions, Find the SI units in which the constants A and B expressed.
View SolutionThe refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
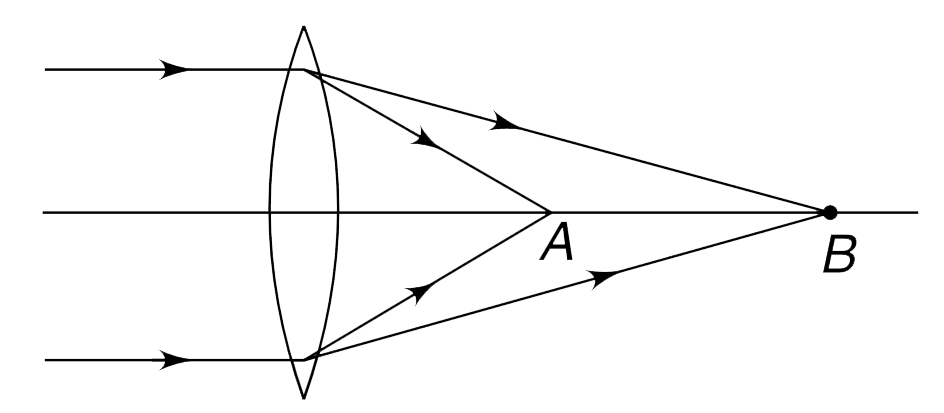
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
View Solution
Knowledge Check
Refractive index (μ) of a medium depends upon
Atemperature of the mediumBwavelength of the incident lightCnature and physical state of the mediumDall the aboveWhen light of wavelength λ travels through glass, the refractive index of glass varies with wavelength as μ=A+Bλ2. What are the dimensional formulae of A and B?
A[M0L0T0][M0L2T−1]B[M0L1T−1][M0L2T0]C[M0L0T0][M0L2T0]D[M1L0T1][M0L1T1]The refractive index of a medium is given by μ=A+Bλ2 where A and B are constants and λ is the wavelength of light.
Then the dimensions of B are the same as that ofAWavelengthBAreaCVolumeDVelocity
The correct curve between refractive index μ and wavelength λ will be

View SolutionSuppose refractive index μ is given as μ=A+Bγ2 where A and B are constants and γ is wavelength, then dimensions of B are same as that of
View SolutionHow does refractive (µ) of a material vary with respect to wavelength (λ)? A and B are constants
View SolutionRefractive index mu is given as μ=A+Bλ2, where A and B are constants and lambda is wavelength, then dimensions of B are same as that of
View SolutionThe correct curve between refractive index μ and wavelength λ will be

View Solution
