The refractive index of air with respect to glass is expressed as gμa=sinisinr.
(a) Write down a similar expression for aμg in terms of the angles i and r.
(b) if angle r=90∘, what is the corresponding angle i called ?
(c) What is the physical significance of the angle i in part (b) ?
The correct Answer is:(a) aμg=sinrsini,
(b) critical angle,
(c) If angle of incidence exceeds the value of i obtained in part (b), total internal reflection occurs.
Let's solve the question step by step.
Step 1: Write down the expression for the refractive index of air with respect to glass.
The refractive index of air with respect to glass is given by:
μag=sinisinr
Step 2: Write down a similar expression for μga.
To find the expression for μga, we take the inverse of the original equation. Thus, we have:
μga=sinrsini
Step 3: Analyze the case when r=90∘.
If the angle of refraction r is 90∘, we can substitute this value into our expression for μga:
μga=sin(90∘)sini=1sini
Step 4: Identify the corresponding angle i when r=90∘.
When r=90∘, the angle i is referred to as the critical angle, denoted by ic.
Step 5: Discuss the physical significance of the critical angle.
The physical significance of the critical angle ic is that it marks the boundary between refraction and total internal reflection. When the angle of incidence i is greater than the critical angle ic, total internal reflection occurs, meaning that all the light is reflected back into the medium rather than being refracted.
Summary of the Solution:
(a) The expression for μga is:
μga=sinrsini
(b) The corresponding angle i when r=90∘ is called the critical angle ic.
(c) The physical significance of the critical angle ic is that it is the angle of incidence above which total internal reflection occurs.
---
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D) MULTIPLE CHOICE TYPE
3 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) NUMERICALS
3 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
The refractive index of water with respect to air is aμw and of glass with respect to air is aμg. Express the refractive index of glass with respect to water.
View SolutionRefractive index of a glass as light ray passes from air to glass is given by n=sinisinr. In a centain experiment , I and r ware found to be 45∘±3∘and30∘±3∘, then error in n is nearly
View SolutionA point source S is placed at the bottom of different layers as shown in the figure. The refractive index of bottom most layer is μ0. The refractive index of any other upper layer is μ(n)=μ0−μ04n−18 where n=1,2………….A ray of light with angle i slightly more than 30∘ starts from the source S. Total internal reflection takes place at the upper surface of a layer having n equal to

View SolutionUse the given figure to express :
(i) a in terms of b and f,
(ii) e in terms of f and g,
(iii) d in terms of a and e,
(iv) c in terms of e and g.
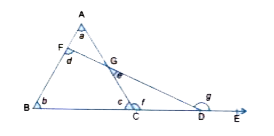
View Solution
In the adjacent diagram, AO is a ray of light incident on a rectangular glass slab.
(a) Complete the path of the ray till it emerges out of the slab.
(b) In the diagram, mark the angle of incidence (i) and the angle of refraction (r) at the first interface. how is the refractive index of glass related to the angles i and r ?
(c) Mark angle of emergence by the letter e. how are the angles i and e related ?
(d) Which two rays are parallel to each other ? Name them
(e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray. state one factor that affects the lateral displacement.
View Solution(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of a triangular glass prisms in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of prism is √2
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View SolutionA ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction, and (ii) the angle of deviation for the ray ?
View Solution
