Draw a neat labelled ray diagram to show total internal reflection of a ray of light incident normally on one face of a 30∘,90∘,60∘ prism.
To solve the problem of drawing a neat labeled ray diagram to show total internal reflection of a ray of light incident normally on one face of a 30∘,90∘,60∘ prism, follow these steps:
1. Draw the Prism: Start by sketching a right-angled prism with angles 30∘, 60∘, and 90∘. Label the vertices as A, B, and C where A is the vertex with 30∘, B is the vertex with 90∘, and C is the vertex with 60∘.
2. Incident Ray: Draw a ray of light that strikes the face AB of the prism normally (at a 90∘ angle). Since it is normal incidence, the angle of incidence is 0∘.
3. Draw the Normal Line: At the point where the ray strikes face AB, draw a normal line perpendicular to that face. This line will help in visualizing the angles of incidence and refraction.
4. Refraction at Face AB: Since the ray strikes normally, it will pass straight through the prism without bending. Mark the point where the ray exits face AC.
5. Angle of Incidence at Face AC: Now, at face AC, determine the angle of incidence. Since the internal angle at vertex B is 90∘, and the angle at vertex C is 60∘, the angle of incidence at face AC will be 60∘ (because the total angle around point B is 180∘).
6. Total Internal Reflection: Since the angle of incidence (60∘) is greater than the critical angle for glass (approximately 42∘), total internal reflection will occur. Draw the reflected ray inside the prism at an angle of 60∘ to the normal at face AC.
7. Exit Ray: Finally, draw the ray as it exits the prism from face BC. Since the angle of incidence at face BC is 30∘ (the remaining angle in the triangle), which is less than the critical angle, the ray will refract out of the prism.
8. Label the Diagram: Clearly label all the parts of the diagram: the incident ray, reflected ray, refracted ray, normals, angles of incidence, and the angles of the prism.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D) MULTIPLE CHOICE TYPE3videos
REFRACTION OF LIGHT AT PLANE SURFACES
- BOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) NUMERICALS3videos
REFRACTION OF LIGHT AT PLANE SURFACES
- BOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:5videos
REFRACTION OF LIGHT
- BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)2videos
REFRACTION THROUGH A LENS
Similar Questions
Draw a diagram to show the reflection of a light ray incident normally on a plane mirror.
View SolutionDraw a labelled ray diagram to illustrate (a) critical angle (b) total internal reflection for a ray of light moving from one medium to another.
View SolutionDraw a ray diagram to illustrate how a ray of light incident obliquely on one face of a rectangular glass slab of uniform thickness emerges.
View SolutionComplete the following diagrams in Fig. by drawing the reflected ray for the incident rays A and B.
 View Solution
View SolutionDraw a neat and labelled diagram, when a ray of white light passes through an equilateral prism.
View SolutionDraw the incident ray and the reflected ray. if a light ray is incident on a plane mirror with the angle of incidence 30∘.
View SolutionDraw a diagram to show the reflection of a ray of light by a plane mirror. In the diagram, label the incident ray, the reflected ray, the normal, the angle of incidence and the angle of reflection.
View SolutionA ray of light falls normally on one face of a right angled prims of refracting angle A. It suffers two total internal reflections before coming out of prism parallel to incident ray as shown. Refractive index to prism material will be:
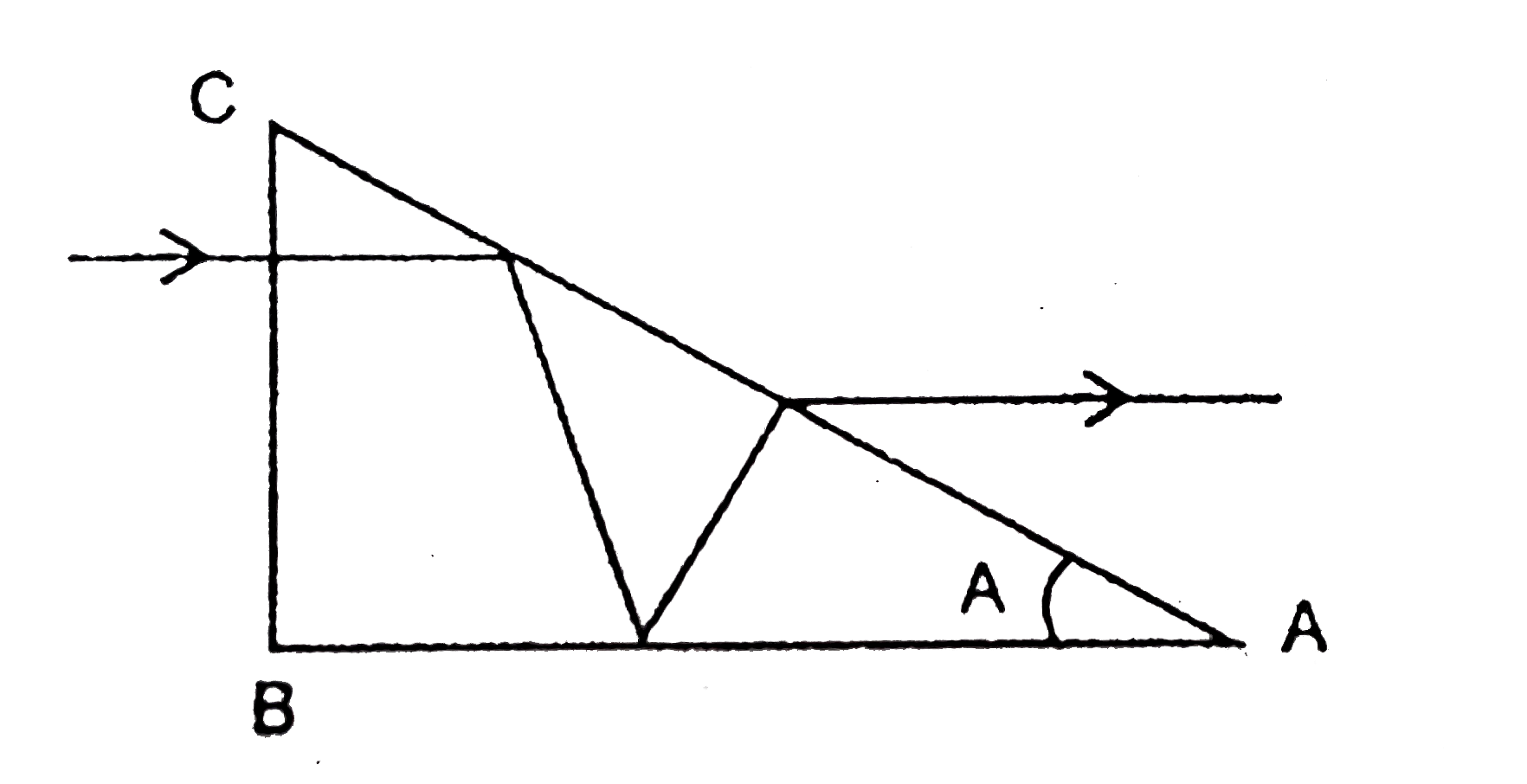 View Solution
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
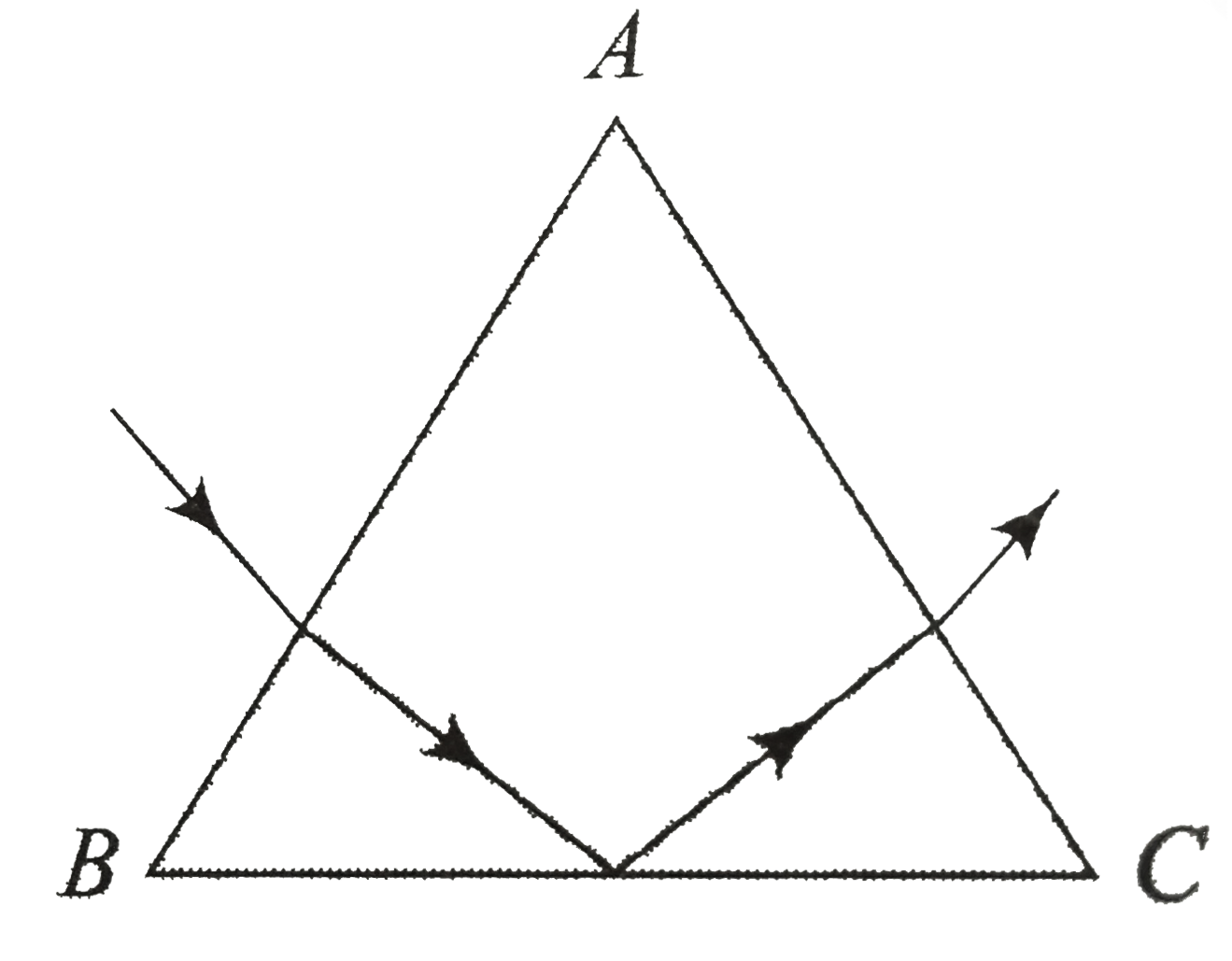 View Solution
View Solution(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of a triangular glass prisms in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of prism is √2View Solution

