The refractive index of glass is 1⋅5 from a point P inside a glass slab, draw rays PQ, PB and PC incident on the glass-air surface at an angle of incidence 30∘,42∘and60∘ respectively.
(a) In the diagram show the approximate direction
of these rays as they emerge out of the slab.
(b) What is the angle of refraction for the ray PB
(Take sin42∘=23)
The correct Answer is:(b) 90∘.
To solve the problem step by step, we will first address part (a) by drawing the rays and then move on to part (b) to calculate the angle of refraction for ray PB.
2. Draw the glass slab:
- Draw a horizontal line to represent the glass-air interface. Label the top part as "Air" and the bottom part as "Glass".
3. Draw the incident rays:
- From point P inside the glass slab, draw ray PQ making an angle of 30° with the normal at the interface.
- Draw ray PB making an angle of 42° with the normal.
- Draw ray PC making an angle of 60° with the normal.
4. Determine the direction of the rays as they emerge:
- For ray PQ (i1 = 30°): Use Snell's law to find the angle of refraction (r1) as it exits into the air.
- For ray PB (i2 = 42°): This ray is at the critical angle, so it will emerge parallel to the interface.
- For ray PC (i3 = 60°): This ray will undergo total internal reflection since its angle of incidence is greater than the critical angle.
5. Label the emerging rays:
- Draw the emerging ray from PQ at an angle r1 with respect to the normal in the air.
- Draw ray PB emerging parallel to the interface.
- Indicate that ray PC does not emerge but reflects back into the glass.
Part (b): Calculating the Angle of Refraction for Ray PB
1. Use Snell's Law:
- Snell's law states that n1sin(i)=n2sin(r).
- Here, n1 (refractive index of glass) = 1.5, n2 (refractive index of air) = 1, and i=42°.
2. Rearranging Snell's Law:
- We can write it as sin(r)=n1n2sin(i).
- Substituting the values:
sin(r)=1.51sin(42°)
3. Using the given value:
- We know sin(42°)=23.
- Therefore,
sin(r)=1.5×23=1
4. Finding the angle of refraction:
- Since sin(r)=1, this means r=90°.
Final Answers
- (a) The rays PQ, PB, and PC are drawn with their respective directions as they emerge from the slab.
- (b) The angle of refraction for ray PB is 90°.
- Draw a horizontal line to represent the glass-air interface. Label the top part as "Air" and the bottom part as "Glass".
- From point P inside the glass slab, draw ray PQ making an angle of 30° with the normal at the interface.
- Draw ray PB making an angle of 42° with the normal.
- Draw ray PC making an angle of 60° with the normal.
- For ray PQ (i1 = 30°): Use Snell's law to find the angle of refraction (r1) as it exits into the air.
- For ray PB (i2 = 42°): This ray is at the critical angle, so it will emerge parallel to the interface.
- For ray PC (i3 = 60°): This ray will undergo total internal reflection since its angle of incidence is greater than the critical angle.
- Draw the emerging ray from PQ at an angle r1 with respect to the normal in the air.
- Draw ray PB emerging parallel to the interface.
- Indicate that ray PC does not emerge but reflects back into the glass.
1. Use Snell's Law:
- Snell's law states that n1sin(i)=n2sin(r).
- Here, n1 (refractive index of glass) = 1.5, n2 (refractive index of air) = 1, and i=42°.
- We can write it as sin(r)=n1n2sin(i).
- Substituting the values:
sin(r)=1.51sin(42°)
- We know sin(42°)=23.
- Therefore,
sin(r)=1.5×23=1
- Since sin(r)=1, this means r=90°.
- (a) The rays PQ, PB, and PC are drawn with their respective directions as they emerge from the slab.
- (b) The angle of refraction for ray PB is 90°.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(D) MULTIPLE CHOICE TYPE
3 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) NUMERICALS
3 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
A light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View SolutionA ray of light falls normally on a glass slab. Draw a diagram showing the path of the ray till it emerges out of the slab. What is the angle of incidence and angle of refraction at each surface of slab ?
View Solution
Knowledge Check
Unpolarized light is incident on a plane glass surface. The angle of incidence so that reflected and refracted rays and perpendicular to each other, then
Ataniβ=μ2Btaniβ=μCsiniβ=μDcosiβ=μLight is incident on a glass surface at polarising angle of 57.5∘ Then the angle between the incident ray and the refracted ray is
A57.5∘B115∘C205∘D145∘
One side of a glass slab is silvered as shown in the figure. A ray of light is incident on the other side at angle of incidence 45∘. Refractive index of glass is given as √2. The deflection suffered by the ray when it comes out of the slab is
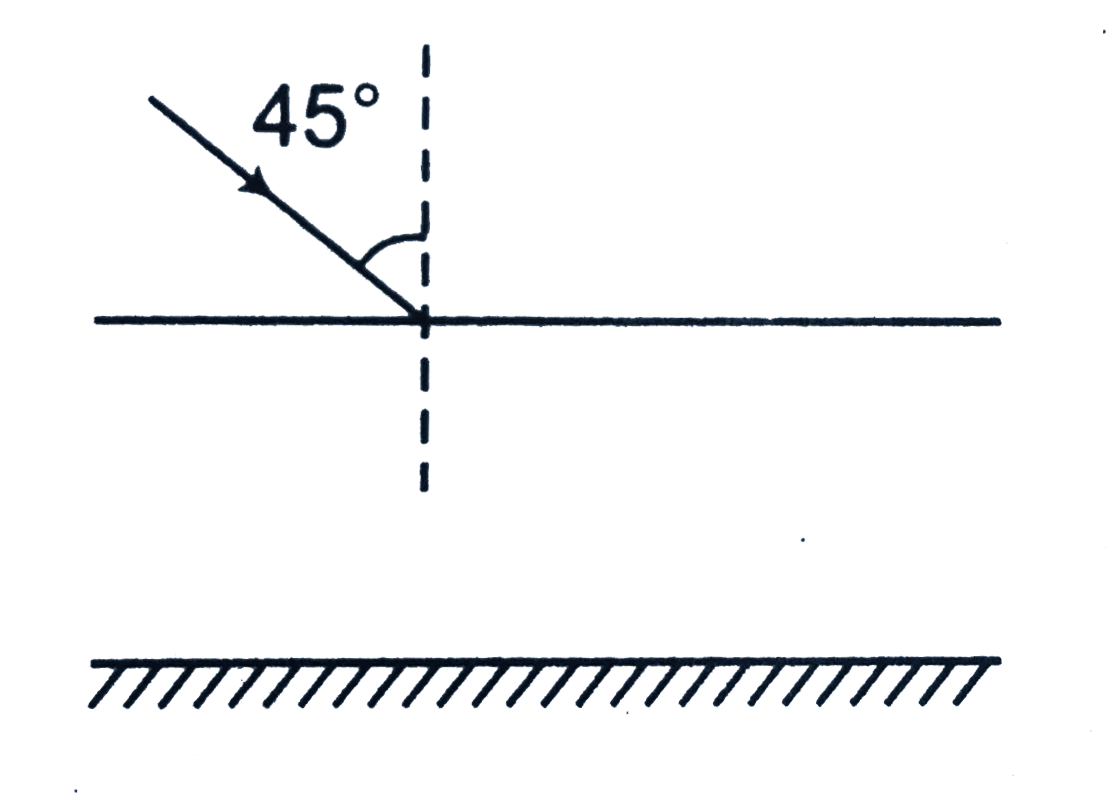
View SolutionOne side of a glass slab is silvered as shown. A ray of light is incident on the other side at angle of incidence i=45∘ . Refractive index of glass is given as 1.5. The deviation of the ray of light from its initial path when it comes out of the slab is

View SolutionOne side of a glass slab is silvered as shown. A ray of light is incident on the other side at angle of incidence i=45∘. Refractive index of glass a is given as 1.5. The diviation of the ray of light from its initial path when it comes out of the slab is

View SolutionUnpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to eachother ?
View SolutionA ray of light falls normally on a rectangular glass slab.
Draw a ray diagram showing the path of the ray till it emerges out of the slab.
View SolutionA ray of light strikes the surface of a rectangular glass slab such that the angle of incidence in air is (i) 0∘,(ii)45∘. In each case, draw a diagram to show the path taken by the ray as it passes through the glass slab and emerges from it.
View Solution
