The region between x=0 and x=L is filled with uniform steady magnetic field B0ˆk. A particle of mass m, positive charge q and velocity v0ˆi travels along x-axis and enters the region of the magnetic field. Neglect the gravity throughout the question.
a. Find the value of l if the particle emerges from the region of magnetic field with its final velocilty at an angel 30∘ to its initial velocity.
b. Find the final velocity of the particle and the time spent by it in the magnetic field, if themagnetic field now extends upto 2.1L.
To solve the problem step-by-step, we will break it down into parts (a) and (b) as given in the question.
Part (a)
Given:
- A particle of mass m, positive charge q, and initial velocity v0^i enters a uniform magnetic field →B=B0^k.
- The particle emerges from the magnetic field at an angle of 30∘ to its initial velocity.
Step 1: Analyze the motion of the charged particle in the magnetic field.
The magnetic force acting on the particle is given by the Lorentz force:
→F=q→v×→B
Here, →v=v0^i and →B=B0^k.
Step 2: Calculate the magnetic force.
Using the right-hand rule, we find:
→F=qv0^i×B0^k=qv0B0(^i×^k)=qv0B0(−^j)=−qv0B0^j
This force acts in the negative y-direction.
Step 3: Determine the radius of the circular motion.
The magnetic force provides the centripetal force required for circular motion:
F=mv2r
Setting the magnetic force equal to the centripetal force:
qv0B0=mv2r
From this, we can express the radius r:
r=mv0qB0
Step 4: Relate the radius to the angle of exit.
At the exit point, the particle makes an angle of 30∘ with the initial velocity. The horizontal distance L can be expressed in terms of r:
L=rcos(30∘)=r√32
Substituting the expression for r:
L=mv0qB0⋅√32
Step 5: Solve for L.
Rearranging gives us:
L=√3mv02qB0
Part (b)
Given:
- The magnetic field now extends up to 2.1L.
Step 1: Determine the final velocity.
Since the particle completes a semicircular path within the magnetic field, when it exits, its velocity will be in the opposite direction:
→vfinal=−v0^i
Step 2: Calculate the time spent in the magnetic field.
The time spent in the magnetic field can be calculated using the distance traveled and the speed:
Distance=Circumference of semicircle=πr
Substituting for r:
Distance=π(mv0qB0)
Now, the time t spent in the magnetic field is:
t=DistanceSpeed=π(mv0qB0)v0=πmqB0
Final Answers:
- Part (a): L=√3mv02qB0
- Part (b): Final velocity →vfinal=−v0^i and time spent t=πmqB0
- A particle of mass m, positive charge q, and initial velocity v0^i enters a uniform magnetic field →B=B0^k.
- The particle emerges from the magnetic field at an angle of 30∘ to its initial velocity.
The magnetic force acting on the particle is given by the Lorentz force:
→F=q→v×→B
Here, →v=v0^i and →B=B0^k.
Using the right-hand rule, we find:
→F=qv0^i×B0^k=qv0B0(^i×^k)=qv0B0(−^j)=−qv0B0^j
This force acts in the negative y-direction.
The magnetic force provides the centripetal force required for circular motion:
F=mv2r
Setting the magnetic force equal to the centripetal force:
qv0B0=mv2r
From this, we can express the radius r:
r=mv0qB0
At the exit point, the particle makes an angle of 30∘ with the initial velocity. The horizontal distance L can be expressed in terms of r:
L=rcos(30∘)=r√32
Substituting the expression for r:
L=mv0qB0⋅√32
Rearranging gives us:
L=√3mv02qB0
- The magnetic field now extends up to 2.1L.
Since the particle completes a semicircular path within the magnetic field, when it exits, its velocity will be in the opposite direction:
→vfinal=−v0^i
The time spent in the magnetic field can be calculated using the distance traveled and the speed:
Distance=Circumference of semicircle=πr
Substituting for r:
Distance=π(mv0qB0)
Now, the time t spent in the magnetic field is:
t=DistanceSpeed=π(mv0qB0)v0=πmqB0
- Part (a): L=√3mv02qB0
- Part (b): Final velocity →vfinal=−v0^i and time spent t=πmqB0
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEY ENGLISHChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
The region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.
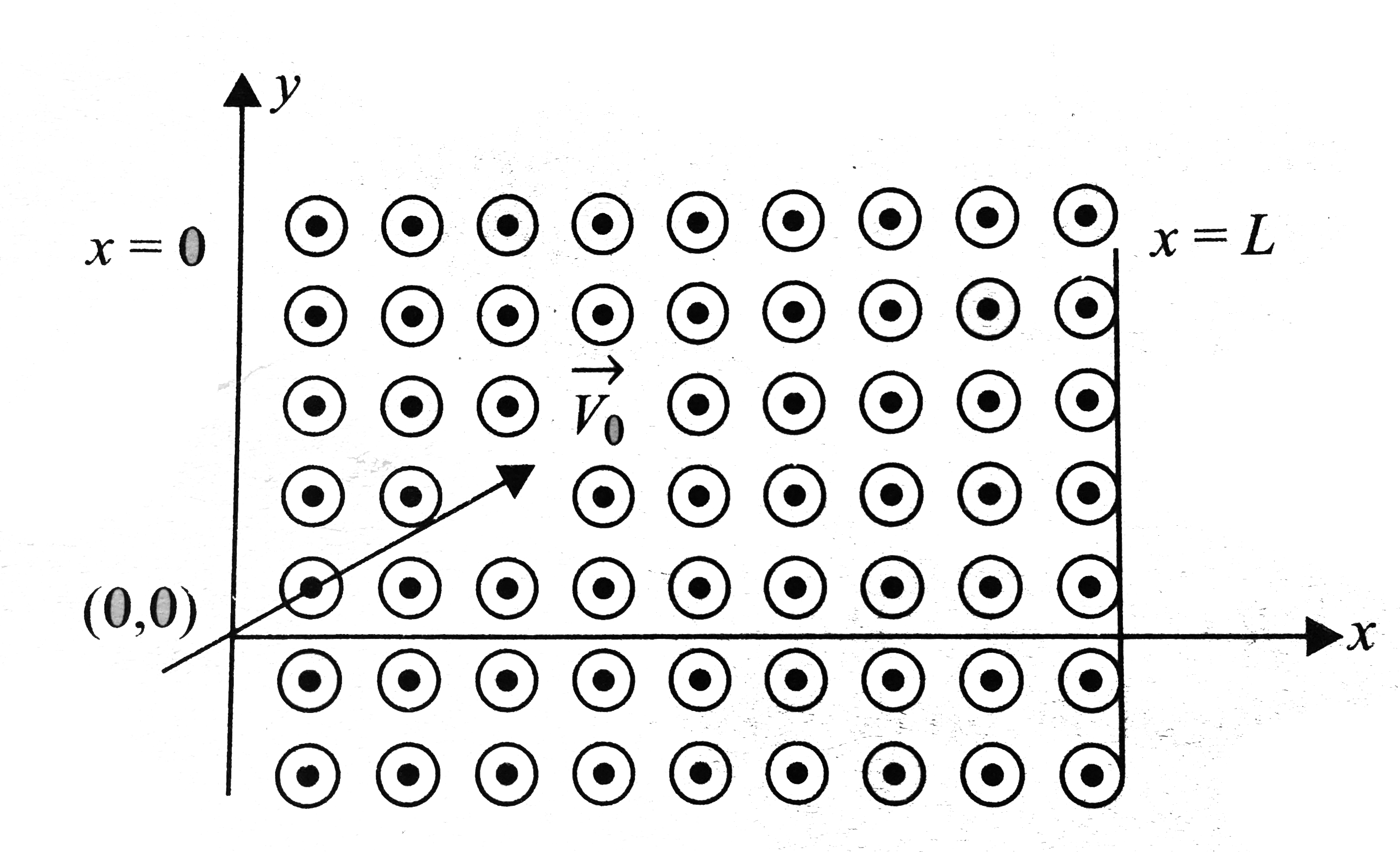
The value of L if the particle emerges from the region of magnetic field with its velocity 100(ms−1)ˆi is
View SolutionThe region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.

The maximum and minimum values of L such that velocity of emerging particle makes angle π/3 with the y-axis are
View SolutionA charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
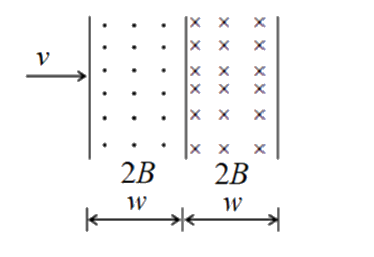
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
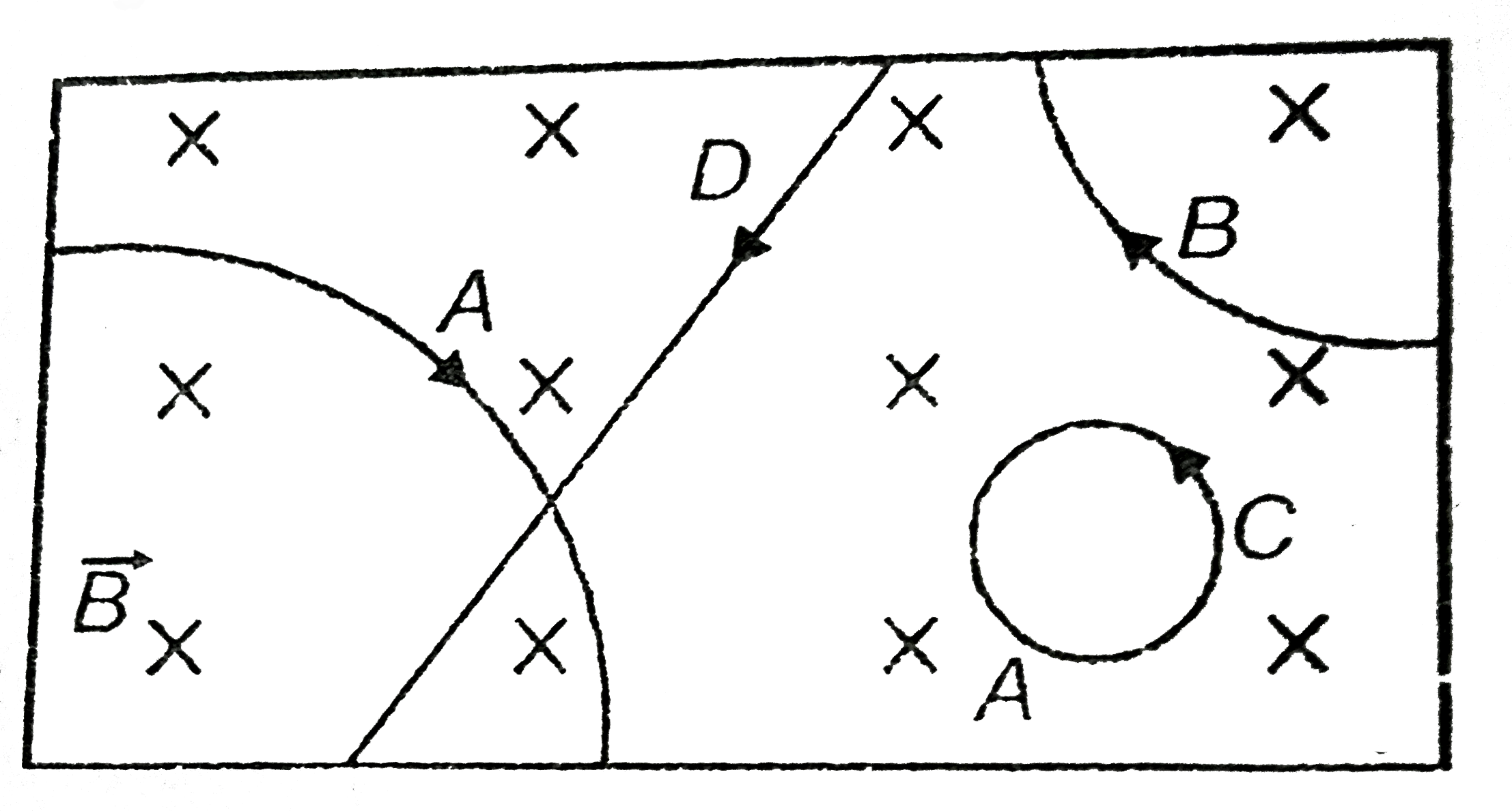
View SolutionA charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force. The path of the particle is a circle. Is this statement true or false?
View Solution
