A charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
an ellipse
straight line
a circle
a heilical
The correct Answer is:D
To determine the path of a charged particle entering a magnetic field at an angle, we can follow these steps:
1. Identify the Given Information:
- A charged particle enters a magnetic field B.
- The initial velocity V makes an angle of 45∘ with the magnetic field B.
2. Resolve the Velocity into Components:
- The velocity can be resolved into two components:
- Component parallel to the magnetic field:
V∥=Vsin(45∘)=V⋅1√2≈0.707V
- Component perpendicular to the magnetic field:
V_{\perpendicular} = V \cos(45^\circ) = V \cdot \frac{1}{\sqrt{2}} \approx 0.707V
3. Analyze the Motion of the Particle:
- The component of velocity parallel to the magnetic field (V∥) will cause the particle to move in a straight line along the direction of the magnetic field.
- The component of velocity perpendicular to the magnetic field ( V_{\perpendicular} ) will cause the particle to undergo circular motion due to the magnetic force acting on it.
4. Combine the Motions:
- The combination of the straight-line motion (due to V∥) and the circular motion (due to V_{\perpendicular} ) results in a helical path.
- The particle moves forward in the direction of the magnetic field while simultaneously moving in a circular path due to the perpendicular component of its velocity.
5. Conclusion:
- Therefore, the path of the charged particle will be helical.
Final Answer:
The path of the particle will be helical.
- A charged particle enters a magnetic field B.
- The initial velocity V makes an angle of 45∘ with the magnetic field B.
- The velocity can be resolved into two components:
- Component parallel to the magnetic field:
V∥=Vsin(45∘)=V⋅1√2≈0.707V
- Component perpendicular to the magnetic field:
V_{\perpendicular} = V \cos(45^\circ) = V \cdot \frac{1}{\sqrt{2}} \approx 0.707V
- The component of velocity parallel to the magnetic field (V∥) will cause the particle to move in a straight line along the direction of the magnetic field.
- The component of velocity perpendicular to the magnetic field ( V_{\perpendicular} ) will cause the particle to undergo circular motion due to the magnetic force acting on it.
- The combination of the straight-line motion (due to V∥) and the circular motion (due to V_{\perpendicular} ) results in a helical path.
- The particle moves forward in the direction of the magnetic field while simultaneously moving in a circular path due to the perpendicular component of its velocity.
- Therefore, the path of the charged particle will be helical.
The path of the particle will be helical.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II
79 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A charged particle moves in a magnetic field →B=10ˆi with initial velocity →u=5→i+4ˆj. The path of the particle will be
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View SolutionA charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force. The path of the particle is a circle. Is this statement true or false?
View SolutionA charged particle of mass m & charge q enters a zone of uniform magnetic field B with a velocity v making an angle θ with the boundary of the zone, having width d, when the particle penetrates half-way into the zone, the change in energy of the particel is
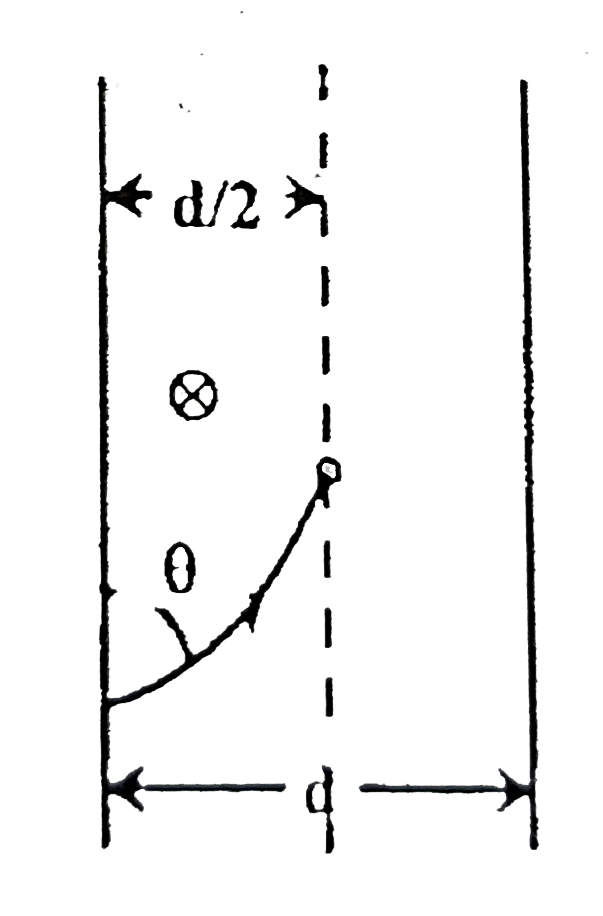
View SolutionAssertion: A charged particle enters in a magnetic field B=B0ˆiwithvelocityv=v0ˆi+v0ˆj, then minimum speed of charged particle may be v0.
Reason: A variable acceleration particle may be v0.
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
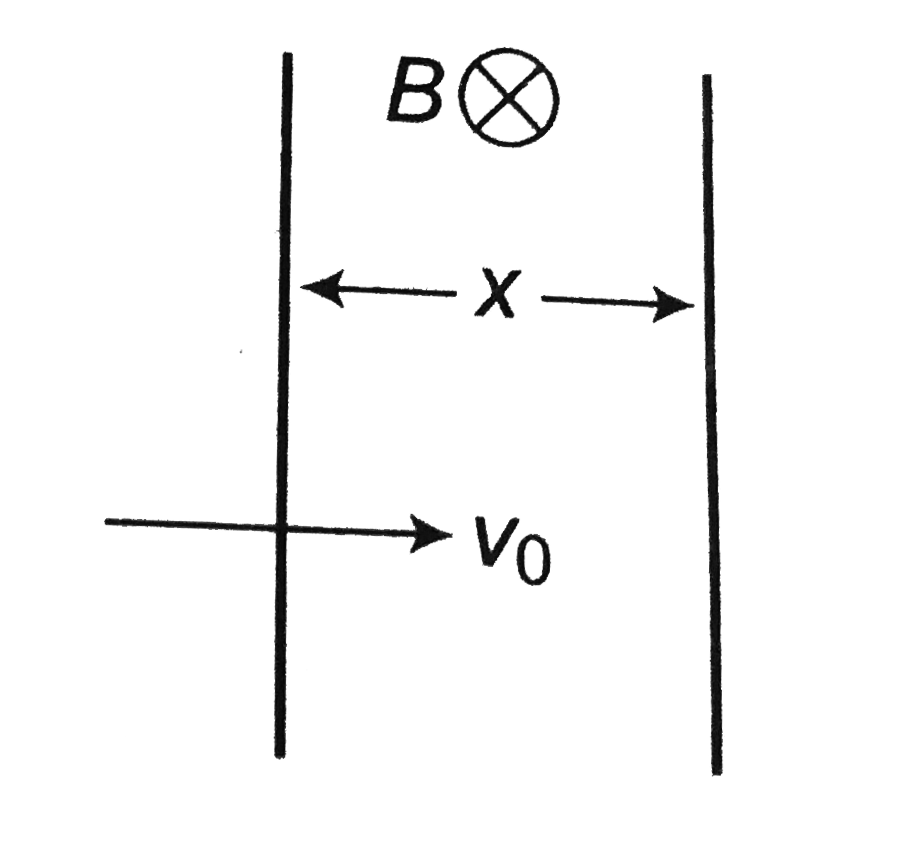
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA particle enters uniform constant magnetic field region with is initial velocity parallel to the field direction. Which of the following statements about its velocity is correct ?(neglect the effects of other fields )
View SolutionA proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
View Solution
