The relaxation time τ is nearly independent of applied electric field E whereas it changes significiantly with temperature T. First fact is (in part) responsible for Ohm's law whereas the second fact leads to variation of p with temperature. Elaborate why ?
To elaborate on the relationship between relaxation time (τ), electric field (E), temperature (T), and their effects on Ohm's law and resistivity (ρ), we can break down the explanation into two main parts:
Part 1: Independence of Relaxation Time from Electric Field and Ohm's Law
1. Understanding Relaxation Time:
- Relaxation time (τ) is the average time between successive collisions of charge carriers (like electrons) in a conductor. It is a measure of how quickly these carriers can respond to an applied electric field.
2. Independence from Electric Field:
- The problem states that τ is nearly independent of the applied electric field E. This means that even if we increase the electric field, the relaxation time does not change significantly.
3. Drift Velocity and Relaxation Time:
- The drift velocity (Vd) of charge carriers in an electric field can be expressed as:
\(
V_d = \frac{eE}{m}τ
\)
- Here, e is the charge of the electron, and m is its mass. If τ remains constant as E changes, then Vd will change linearly with E.
4. Ohm's Law:
- Ohm's law states that the current (I) through a conductor is directly proportional to the voltage (V) across it, given by:
\(
V = IR
\)
- If τ is constant, the resistance (R) remains constant as well, leading to a linear relationship between V and I. This is the essence of Ohm's law.
Part 2: Variation of Resistivity with Temperature
1. Impact of Temperature on Relaxation Time:
- The second part of the question states that τ changes significantly with temperature (T). As temperature increases, the thermal energy of the charge carriers increases, leading to more frequent collisions.
2. Resistivity Formula:
- The resistivity (ρ) of a material can be expressed as:
\(
ρ = \frac{m}{n e^2 τ}
\)
- Here, n is the number density of charge carriers. If τ changes significantly with temperature, it will directly affect the resistivity.
3. Temperature Dependence:
- As temperature increases, if τ decreases (due to increased collisions), the resistivity ρ will also decrease, assuming n and e remain constant. This explains why resistivity varies with temperature.
4. Conclusion:
- The independence of τ from E supports Ohm's law by keeping resistance constant, while the dependence of τ on T explains the variation of resistivity with temperature.
Summary
- Ohm's Law: τ independent of E → constant resistance → linear V−I relationship.
- Resistivity Variation: τ dependent on T → changes in resistivity with temperature.
- Relaxation time (τ) is the average time between successive collisions of charge carriers (like electrons) in a conductor. It is a measure of how quickly these carriers can respond to an applied electric field.
- The problem states that τ is nearly independent of the applied electric field E. This means that even if we increase the electric field, the relaxation time does not change significantly.
- The drift velocity (Vd) of charge carriers in an electric field can be expressed as:
\(
V_d = \frac{eE}{m}τ
\)
- Here, e is the charge of the electron, and m is its mass. If τ remains constant as E changes, then Vd will change linearly with E.
- Ohm's law states that the current (I) through a conductor is directly proportional to the voltage (V) across it, given by:
\(
V = IR
\)
- If τ is constant, the resistance (R) remains constant as well, leading to a linear relationship between V and I. This is the essence of Ohm's law.
- The second part of the question states that τ changes significantly with temperature (T). As temperature increases, the thermal energy of the charge carriers increases, leading to more frequent collisions.
- The resistivity (ρ) of a material can be expressed as:
\(
ρ = \frac{m}{n e^2 τ}
\)
- Here, n is the number density of charge carriers. If τ changes significantly with temperature, it will directly affect the resistivity.
- As temperature increases, if τ decreases (due to increased collisions), the resistivity ρ will also decrease, assuming n and e remain constant. This explains why resistivity varies with temperature.
- The independence of τ from E supports Ohm's law by keeping resistance constant, while the dependence of τ on T explains the variation of resistivity with temperature.
- Ohm's Law: τ independent of E → constant resistance → linear V−I relationship.
- Resistivity Variation: τ dependent on T → changes in resistivity with temperature.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - MCQs (More than one options)
5 Videos
- COMMUNICATION SYSTEMBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - LONG ANSWER TYPE QUESTION
5 Videos
Similar Questions
Dependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
When CaCO3 is heated to a high temperature , it undergoes decomposition into CaO and CO2 whereas it is quite stable at room temperature . The most likely explanation of it, is
View SolutionElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature TC(0). An interesting property of super conductors is that their critical temperature becomes smaller than TC(0) if they are placed in a magnetic field, i.e., the critical temperature TC(B) is a function of the magnetic field strength B. The dependence of TC(B) on B is shown in the figure.
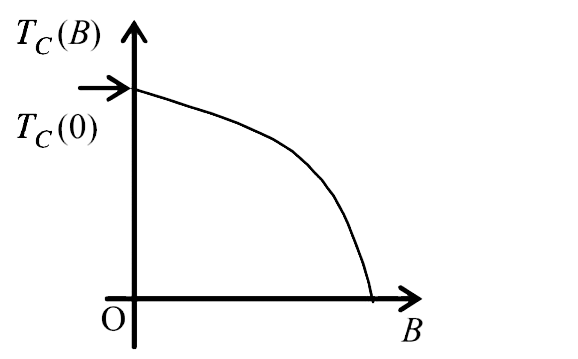 .
.
In the graphs below, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic fields B1(solid line) and B2 (dashed line). If B2 is larget than B1 which of the following graphs shows the correct variation of R with T in these fields?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
The enthalpy change for a certain rection at 300 K is −15.0 K cal mol−1 . The entropy change under these conditions is −7.2 cal K−1mol−1 . The free energy change for the reaction and its spontaneous/ non-spontaneous character will be
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.050kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, above what temperature will the reaction become spontaneous?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=−40Kcal at 400 k cal mol−1. The reaction is spontaneous, below this temperature , it is not . The values fo ΔG and ΔS at 400 k are respectively
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 25∘,X2O4(l)→2XO2(g)
ΔH=2.1Kcal and ΔS=20calK−1. The reaction would be
View SolutionAn insulting container of volume 2V0 is divided in two equal parts by a diathermic (conducting) fixed piston. The left part contains one mole of monoatomic ideal gas whereas right part contains two moles of the same gas. Initial pressue on each side is P0. The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) initial temperature in the two sides, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
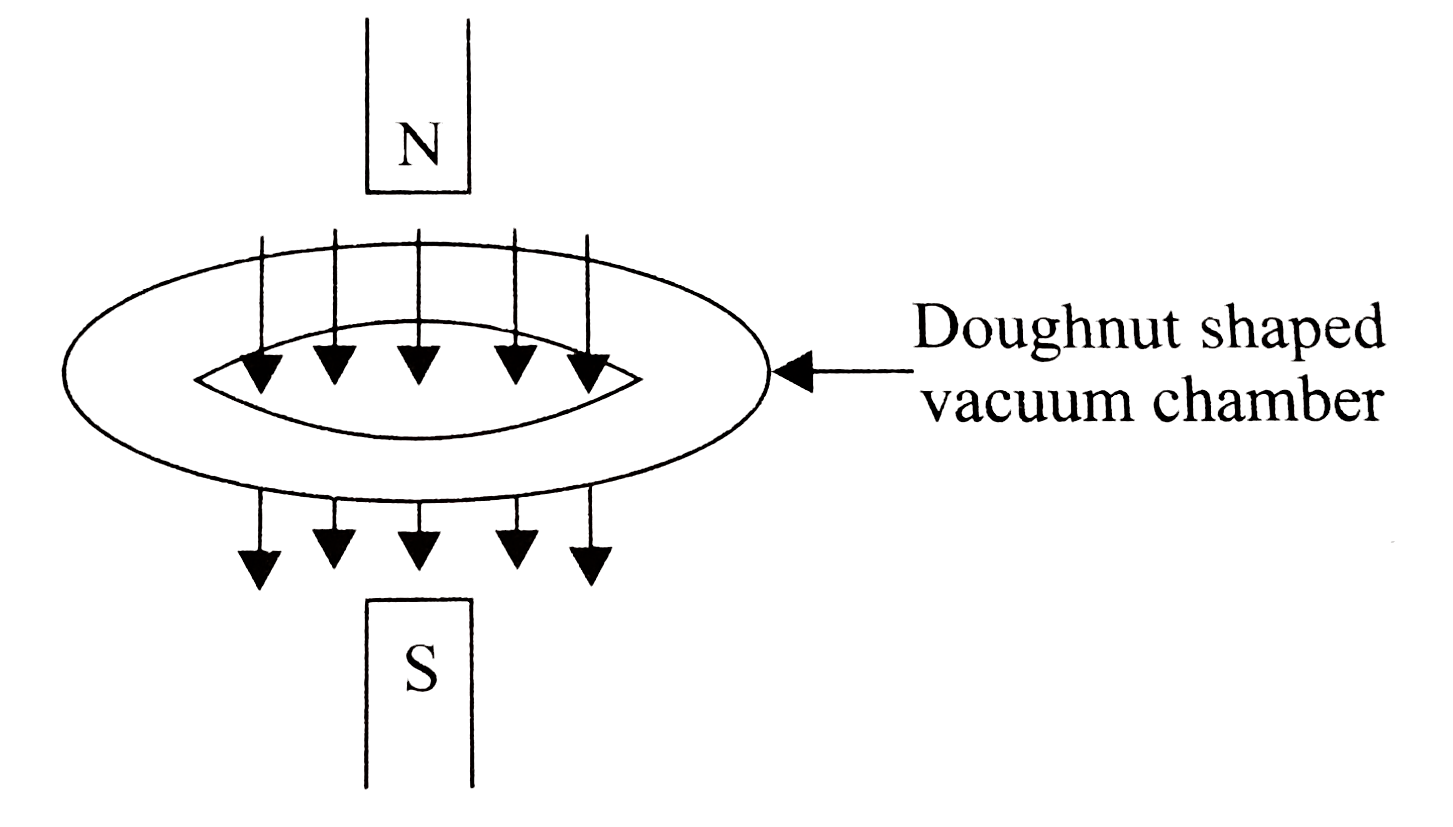
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic flux
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
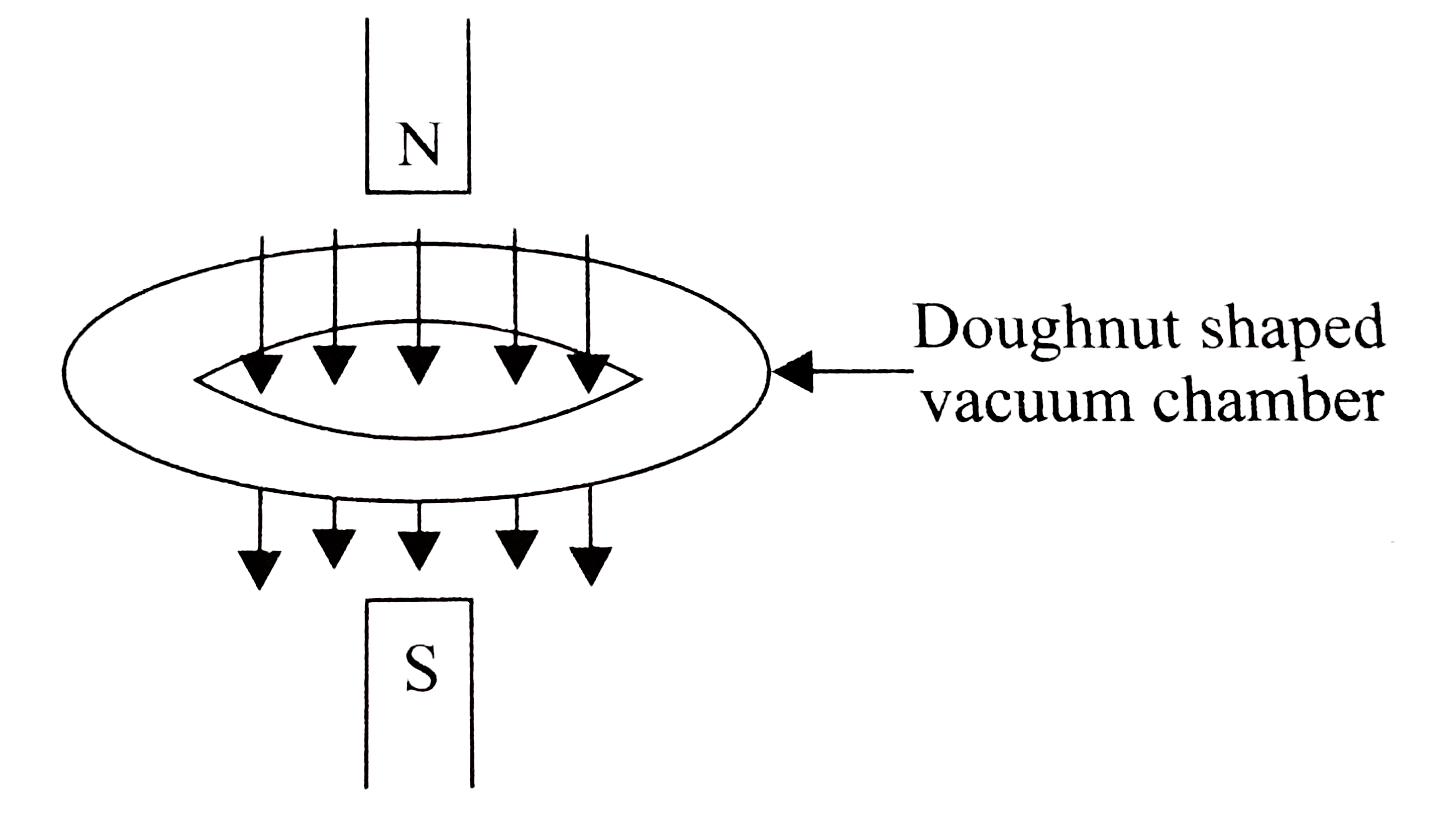
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path must
View SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
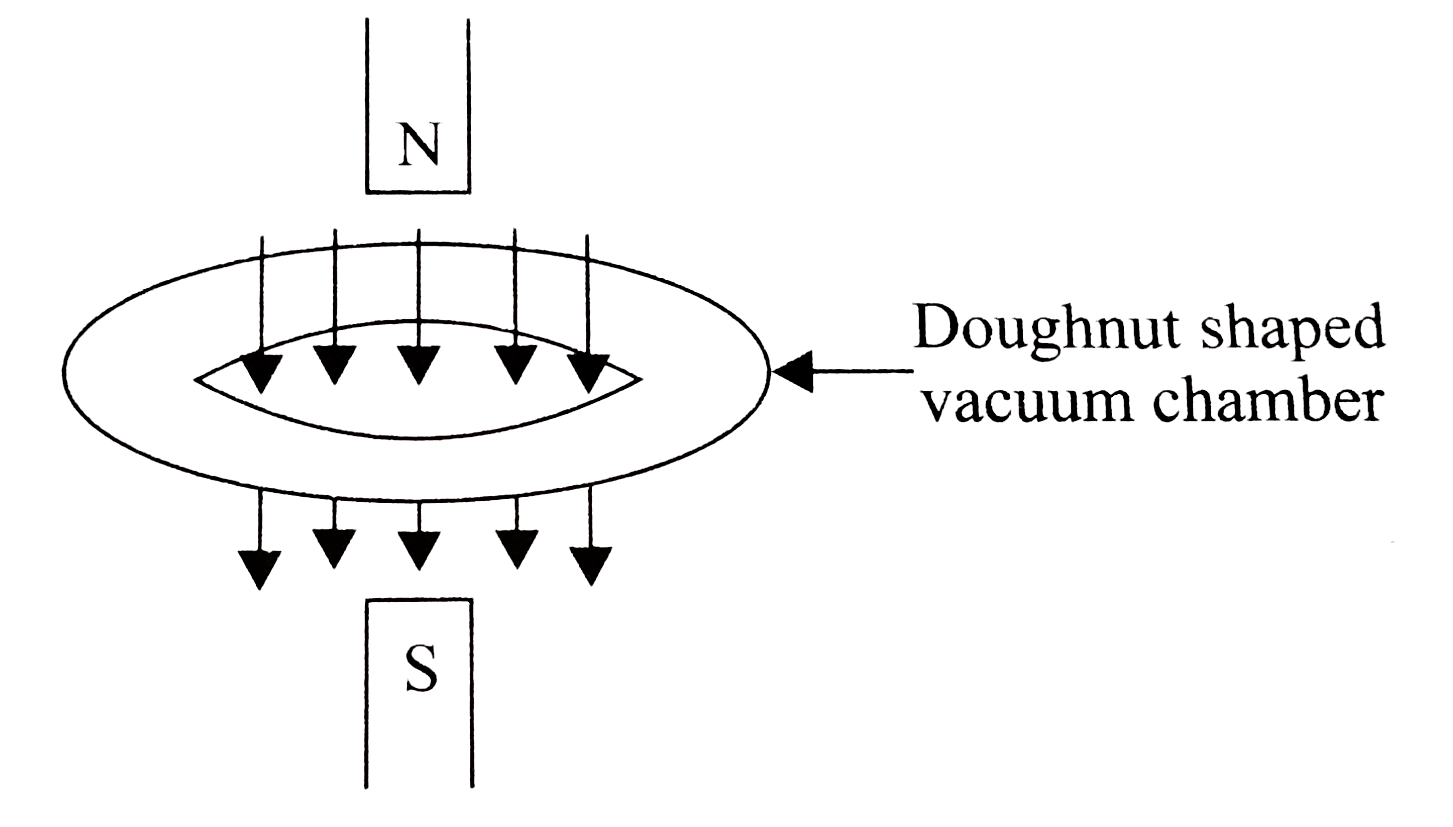
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?
View Solution