Question

The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.

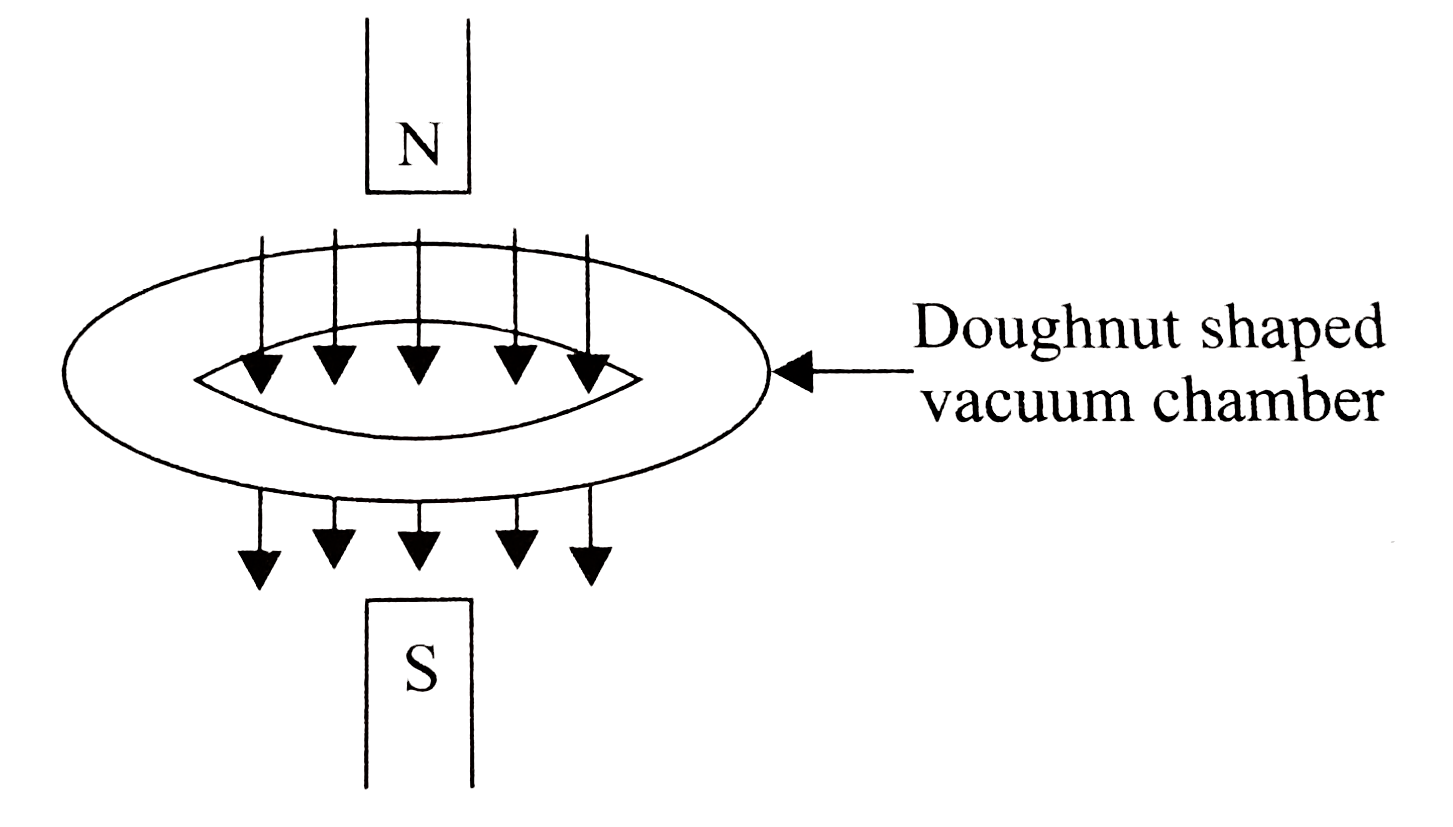
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by ${\displaystyle 2\pi aE=d\left(\varphi \right)/dt}$, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or ${\displaystyle m{v}^2/a=qvB}$ then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ${\displaystyle \epsilon =(d\left(\varphi \right)/dt)}$. Its energy after 'n' trips around the loop will be ${\displaystyle q\left(n\left(\epsilon \right)\right)}$.
Variable magnetic flux

Options

A. can chane sinusoidally
B. should either increase or decrease all the time
C. must becomes zero when induced field is maximum
D. none of these

Answer

B

Explanation

To produce electric field in one direction, magnetic flux should either increase or decrease all the time.