The remaining volume of a glass vessel is constant at all temperature if 1x of its volume is filled with mercury. The coefficient of volume expansion of mercury is 7 times that of glass. The value of x should be
5
7
6
8
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the volume expansions of mercury and glass in the context of the given conditions.
1. Understanding the Problem:
We have a glass vessel that has a constant remaining volume when filled with mercury. The volume expansion coefficient of mercury is 7 times that of glass. We need to find the value of x such that 1x of the vessel's volume is filled with mercury.
2. Initial Volume Setup:
Let the total volume of the glass vessel be V. The volume filled with mercury is Vx, and the remaining volume of the glass vessel is:
Vremaining=V−Vx=V(1−1x)
3. Volume Expansion Relation:
For the remaining volume to be constant, the expansion of the glass must equal the expansion of the mercury. The volume expansion can be expressed as:
ΔVglass=βgVglassΔT
ΔVmercury=βmVmercuryΔT
where βg is the coefficient of volume expansion for glass and βm=7βg for mercury.
4. Setting Up the Equation:
The volume of glass is the remaining volume:
Vglass=V(1−1x)
The volume of mercury is:
Vmercury=Vx
Therefore, we can write the expansions as:
βgV(1−1x)ΔT=7βg(Vx)ΔT
5. Cancelling Common Terms:
Since ΔT and V are common in both sides, we can cancel them out:
(1−1x)=7(1x)
6. Solving for x:
Rearranging the equation gives:
1−1x=7x
Multiplying through by x to eliminate the fraction:
x−1=7
Thus,
x=8
Final Answer:
The value of x should be 8.
We have a glass vessel that has a constant remaining volume when filled with mercury. The volume expansion coefficient of mercury is 7 times that of glass. We need to find the value of x such that 1x of the vessel's volume is filled with mercury.
Let the total volume of the glass vessel be V. The volume filled with mercury is Vx, and the remaining volume of the glass vessel is:
Vremaining=V−Vx=V(1−1x)
For the remaining volume to be constant, the expansion of the glass must equal the expansion of the mercury. The volume expansion can be expressed as:
ΔVglass=βgVglassΔT
ΔVmercury=βmVmercuryΔT
where βg is the coefficient of volume expansion for glass and βm=7βg for mercury.
The volume of glass is the remaining volume:
Vglass=V(1−1x)
The volume of mercury is:
Vmercury=Vx
Therefore, we can write the expansions as:
βgV(1−1x)ΔT=7βg(Vx)ΔT
Since ΔT and V are common in both sides, we can cancel them out:
(1−1x)=7(1x)
Rearranging the equation gives:
1−1x=7x
Multiplying through by x to eliminate the fraction:
x−1=7
Thus,
x=8
The value of x should be 8.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
Pressure remaining constant, at what temperature the volume of a gas will be double of its volume at 0∘C ?
A100∘CB546∘CC273KD546K
An ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of the gas is-
View SolutionA barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
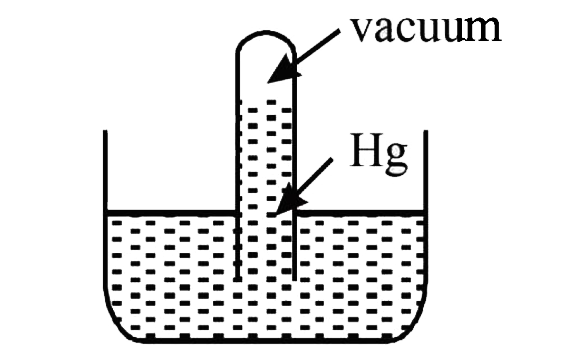
View SolutionState true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
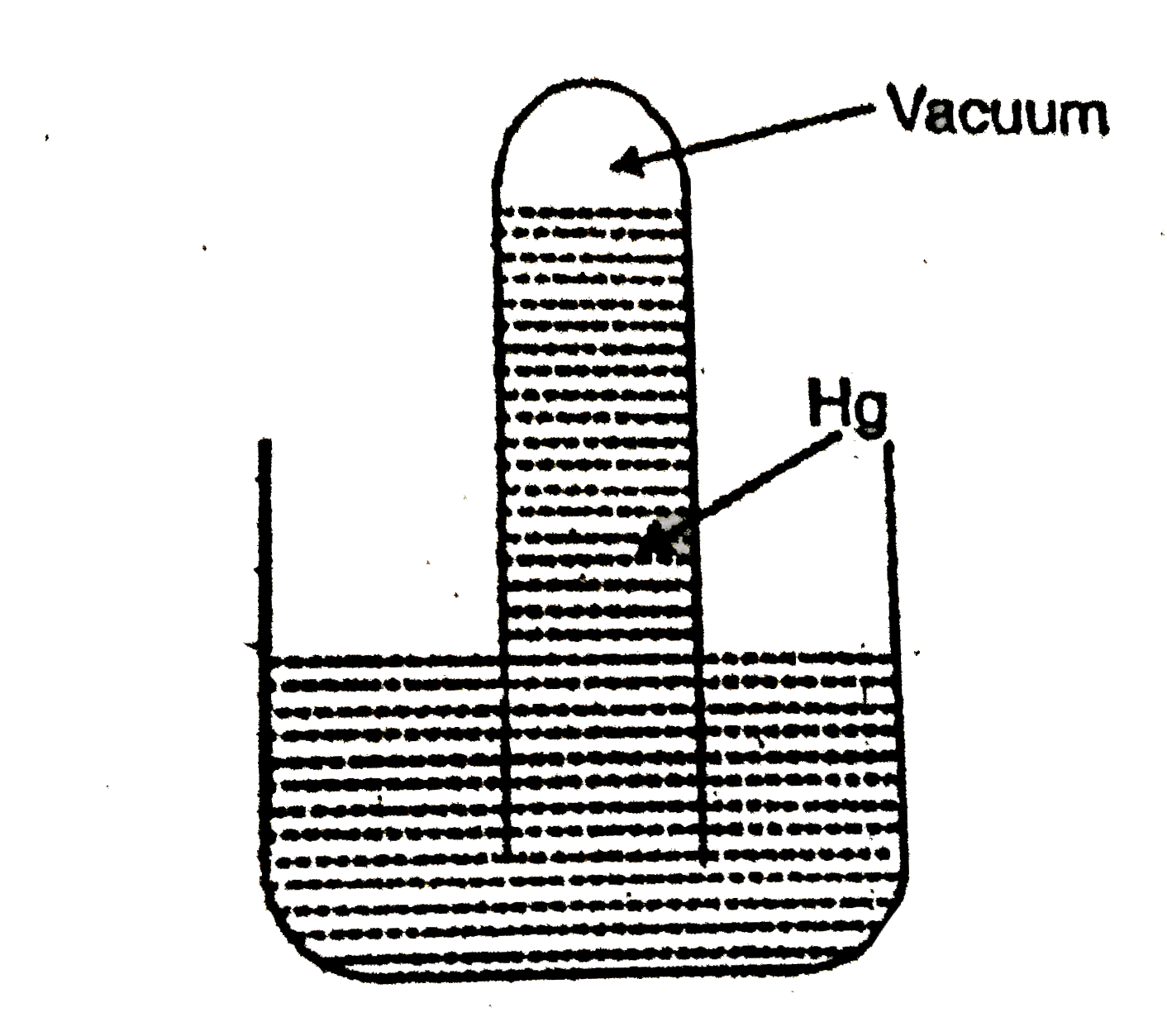
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury could be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4∘C−1 and 9×10−6∘C−1 respectively.
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4C−1 and 9.0×10−6C−1. respectively.
View SolutionWhen a block of iron in mercury at 0∘C, fraction K1of its volume is submerged, while at the temperature 60∘C, a fraction K2 is seen to be submerged. If the coefficient of volume expansion of iron is γFe and that of mercury is γHg, then the ratio (K1)/(K2) can be expressed as
View SolutionA glass vessel measures exactly 10cm xx 10 cm xx 10 cm at 0∘C. It is filled completely with mercury at this temperature. When the temperature is raised to 10∘C, 1.6cm3 of mercury overflows. Calculate the coefficient of volume expansion of mercury. coefficient of linear expansion of glass =6.5×10−6C−1.
View Solution
