The resistance of wire $A B C$ is double of resistance of wire $A D C$ . The magnetic field at $O$ is

Video Solution

Text Solution

Verified by Experts

(a)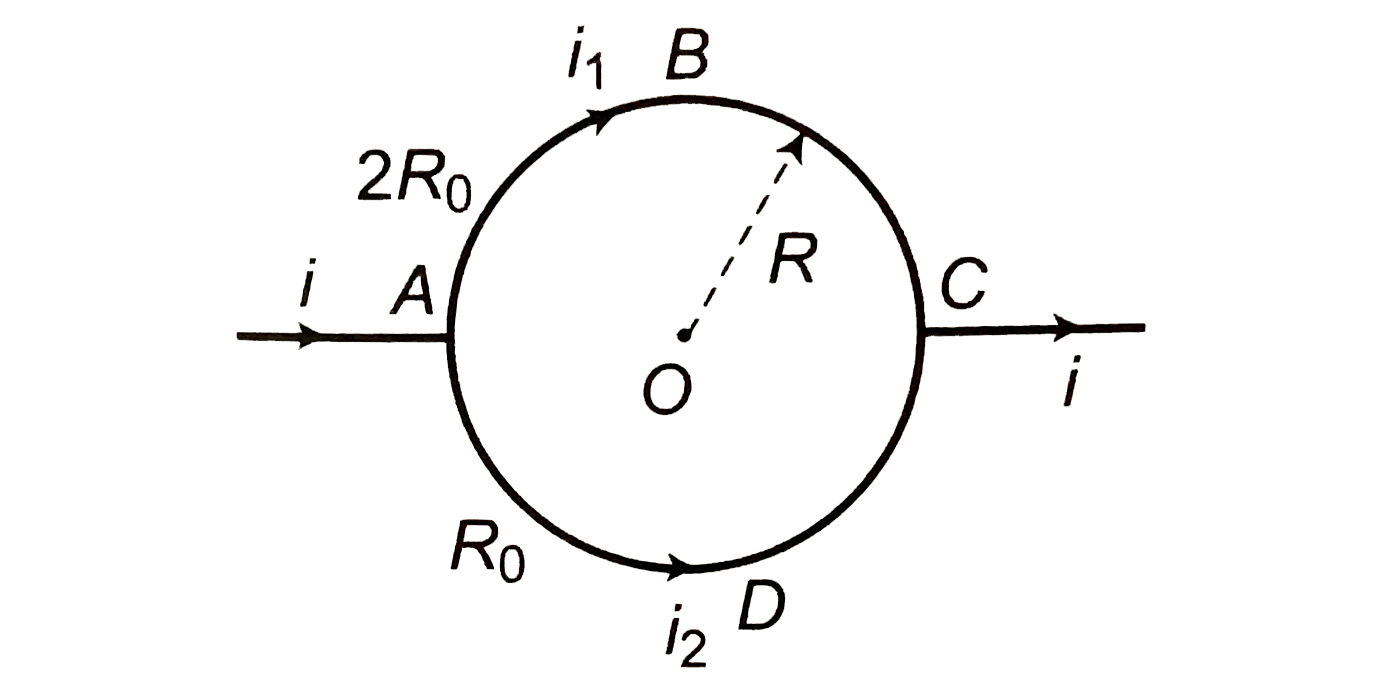
$R_{A B C} = R_{1} = 2 R_{0}, R_{A D C} = R_{2} = R_{0}$
$i_{1} = \frac{R_{0}}{R_{0} + 2 R_{0}} . i = \frac{i}{3}, i_{2} = i - i_{1} = \frac{2 i}{3}$
$B_{1} = \frac{μ_{0} i_{1}}{2 R} \frac{.1}{2} = \frac{μ_{0} i}{12 R}, \otimes$
$B_{2} = \frac{μ_{0} i_{2}}{2 R} \frac{.1}{2} = \frac{μ_{0} i}{6 R}, ⊙$
$B_{O} = B_{2} - B_{1} = \frac{μ_{0} i}{12 R}, ⊙$
(b)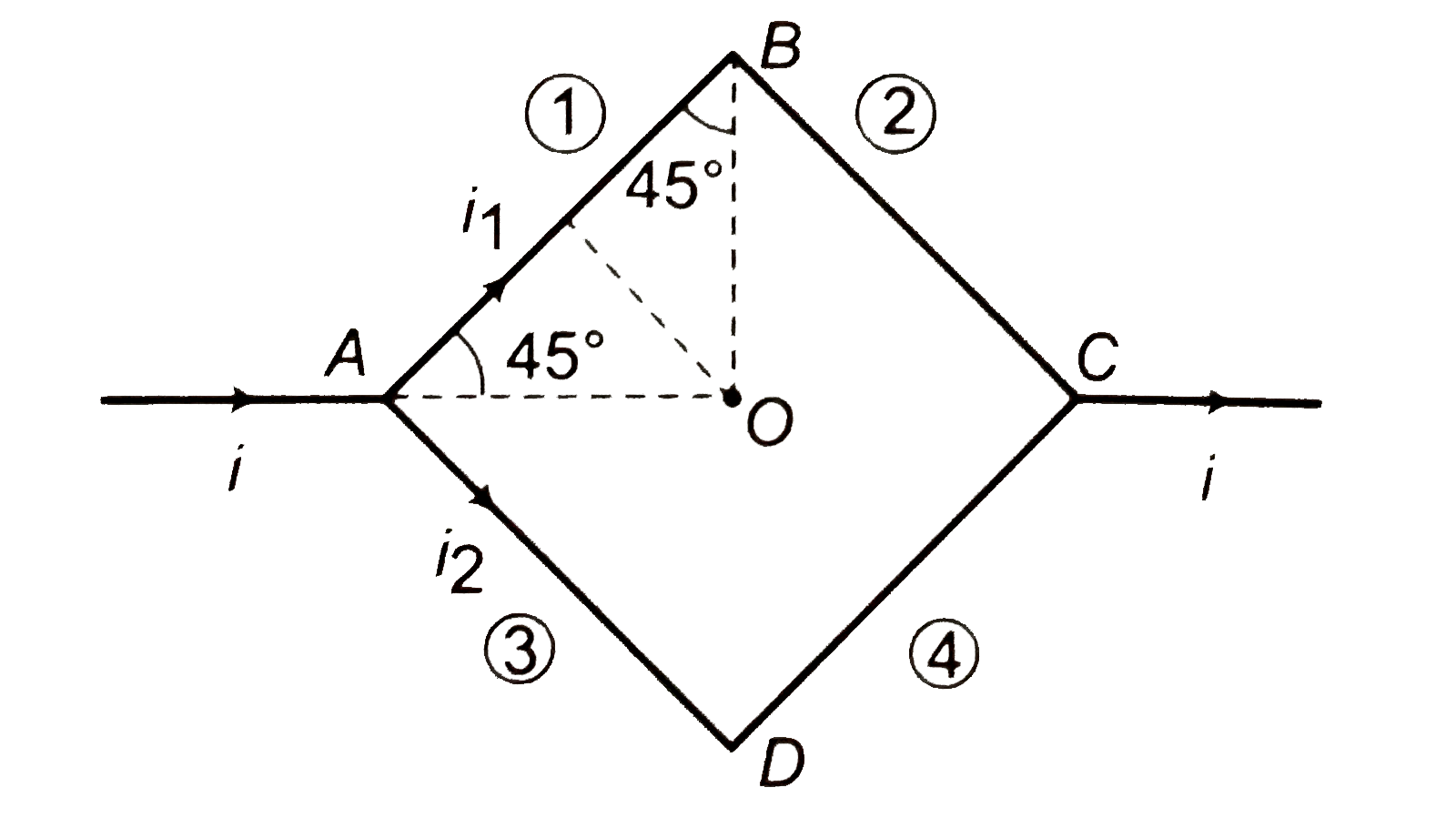
$R_{A B C} = R_{1} = R_{0}, R_{A D C} = R_{2} = R_{0}$
$i_{1} = \frac{2 R_{0}}{R_{0} + 2 R_{0}} i = \frac{2 i}{3}, i_{2} = i - i_{1} = \frac{i}{3}$
$B_{1} = \frac{μ_{0} i_{1}}{4 π d} ({cos 45}^{\circ} + {cos 45}^{\circ}) = \frac{μ_{0} i_{1}}{2 \sqrt{2} π d}$
$= \frac{μ_{0} (2 i / 3)}{2 \sqrt{2} π (\frac{a}{2})} = \frac{2 μ_{0} i}{3 \sqrt{2} π a} = B_{2}, \otimes$
$B_{3} = \frac{μ_{0} i_{2}}{4 π d} ({cos 45}^{\circ} + {cos 45}^{\circ}) = \frac{μ_{0} i_{2}}{2 \sqrt{2} π d}$
$= \frac{μ_{0} (i / 3)}{2 \sqrt{2} π (\frac{a}{2})} = \frac{μ_{0} i}{3 \sqrt{2} π a} = B_{4}, ⊙$
$B_{O} = (B_{1} + B_{2}) - (B_{3} + B_{4})$
$\frac{4 μ_{0} i}{3 \sqrt{2} π a} - \frac{2 μ_{0} i}{3 \sqrt{2} π a}$
$= \frac{\sqrt{2} μ_{0} i}{3 π a}, \otimes$
(c)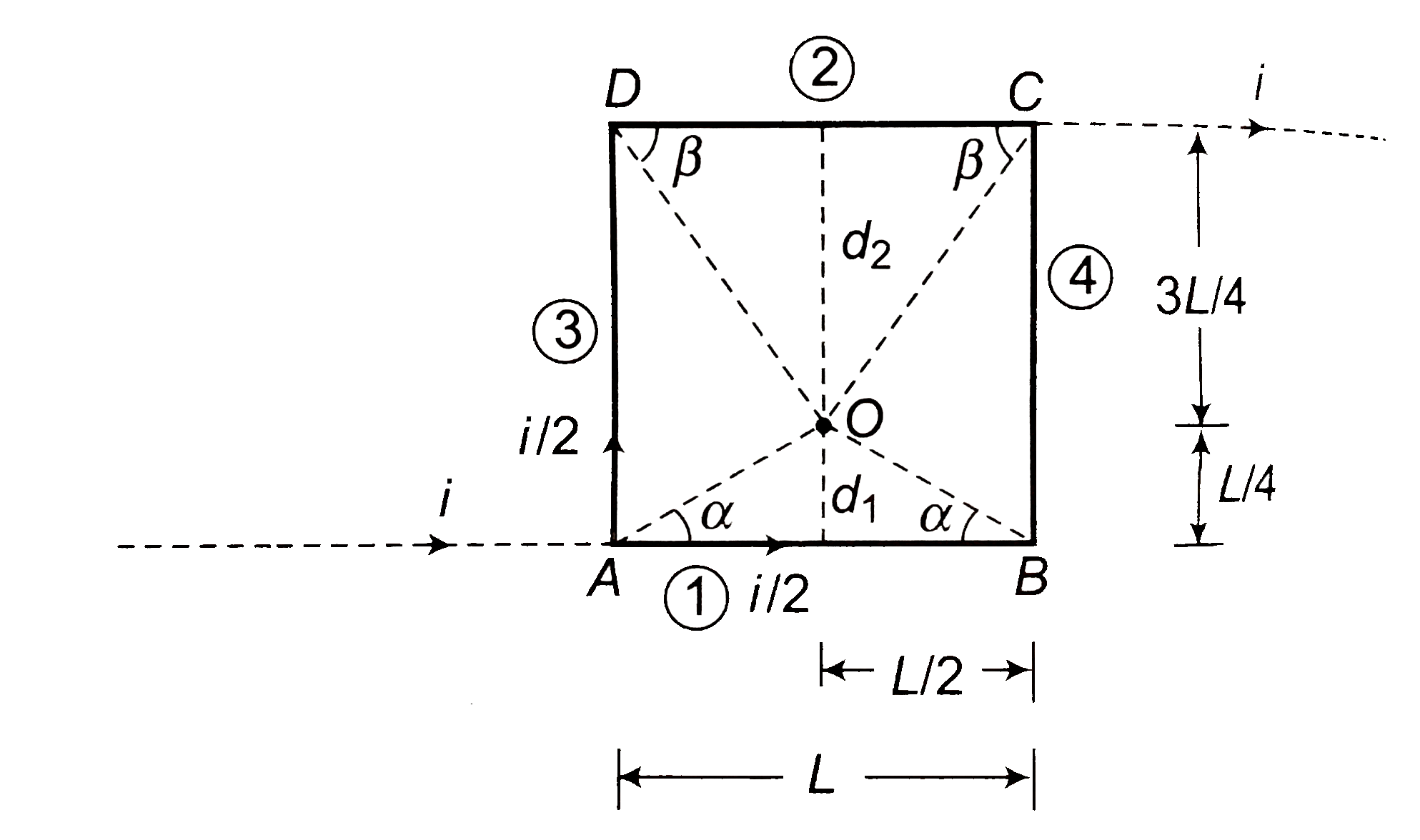
Magnetic field at $O$ :
Due to the wire $A B :$
$d_{1} = L / 4, cos α = \frac{L / 2}{\sqrt{{(L / 2)}^{2} + {(L / 4)}^{2}}} = \frac{2}{\sqrt{5}}$
$B_{1} = \frac{μ_{0} (i / 2)}{4 π d_{1}} [cos α + cos α]$
$= \frac{μ_{0} (i / 2)}{4 π (L / 4)} \times 2 \times \frac{2}{\sqrt{5}} = \frac{2 μ_{0} i}{\sqrt{5} π L}, ⊙$
Due to the wire $D C$
$d_{2} = 3 L / 4, cos β = \frac{L / 2}{\sqrt{{(L / 2)}^{2} + {(L / 4)}^{2}}} = \frac{2}{\sqrt{13}}$
$B_{2} = \frac{μ_{0} (i / 2)}{4 π d_{2}} [cos β + cos β]$
$\frac{μ_{0} (i / 2)}{4 π . (3 L / 4)} \times 2 s s \frac{2}{\sqrt{13}} = \frac{2 μ_{0} i}{3 \sqrt{13} π L}, \otimes$
Magnetic field due to $A D$ is equal and opposite to $B C$
$B_{O} = B_{1} - B_{2} = \frac{2 μ_{0} i}{π L} (\frac{1}{\sqrt{5}} - \frac{1}{2 \sqrt{13}}), ⊙$

Updated on:21/07/2023

The resistance of a wire is
Adirectly proportional to its area of cross-section
Binversely proportional to its area of cross-section
Cindependent of its area of cross-section
Dproportional to square of its area of cross-section
The resistance of the fuse wire is
Alow
Bmoderate
Czero
Dvery high
The resistivity of a wire
AVaries with its length
BVaries with its mass
CVaries with it cross section
DIs independent of length, cross section and mass of the wire