The resostivity of an impurity-free semiconductor at room tempterature is ρ=50Ωcm. It becomes equal to ρ1=40Ωcm. When the semiconductor is illuminated with light, and t=8ms after swithching off the light source the resistivity becomes equal to ρ2=45Ωcm. Find the mean lifetime of conduction electrons and holes.
We write the conductivity of the simple as σ=σi+σγ
where σi= intrinsic conductivity and σγ is the photo conductivity. At t=0, assuming saturation we have
1ρ1=1ρ+σγ0orσγ0=1ρ1−1ρ
Time t after light source is switched off
we have beacuse of recombination of electron and holes in the sample
σ=σi+σγ0e−t/T
where T= mean lifetime of electrons and holes.
Thus Thus1ρ2=1ρ+(1ρ1−1ρ)e−t/T
or 1ρ2−1ρ=(1ρ1−1ρ)e−t/T
or et/T=1ρ1−1ρ1ρ2−1ρ=ρ2(ρ−ρ1)ρ1(ρ−ρ2)
Hence T=t/In{ρ2(ρ−ρ1)ρ1(ρ−ρ2)}
Substitution gives T=9.87ms~0.01sec
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
In Hall effect measurements a plate of width h=10mm and length l=50mm made of p-type semiconductor was placed in a magnetic field with induction B=5.0kG. A potential difference V=10V was applied across the edges of the plate. In this case the hall field is VH=50mV and resistivity ρ=2.5Ω,cm. Find the concentration of holes and hole mobility.
View SolutionρCu=12(μΩ)(cm), ρNi=51(μΩ)(cm). If both conductors have equal length diameter 2mm each and have equivalent resistance of 3Ω. Find l

View Solution
Knowledge Check
An intrinsic semiconductor has a resistivity of 0.50 Ω m at room temperature. Find the intrinsic carrier concentration if the mobilities of electrons and holes are 0.39m2V−1s−1 and 0.11m2V−1s−1 respectively
A1.2×1018/m3B2.5×1019/m3C1.9×1020/m3D3.1×1021/m30.1 M solution of an electrolyte A+B− placed in a conductivity cell wilth electrodes 4 cm apart and each with area of cross-section equal to 2 sq cm was found to have a resistance of 200Ω. The molar conductivity of the solution will be
A25cm2/ΩB100cm2/ΩC0.25cm2/ΩD400cm2/ΩAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
A20ΩB10ΩC60ΩD40Ω
In the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
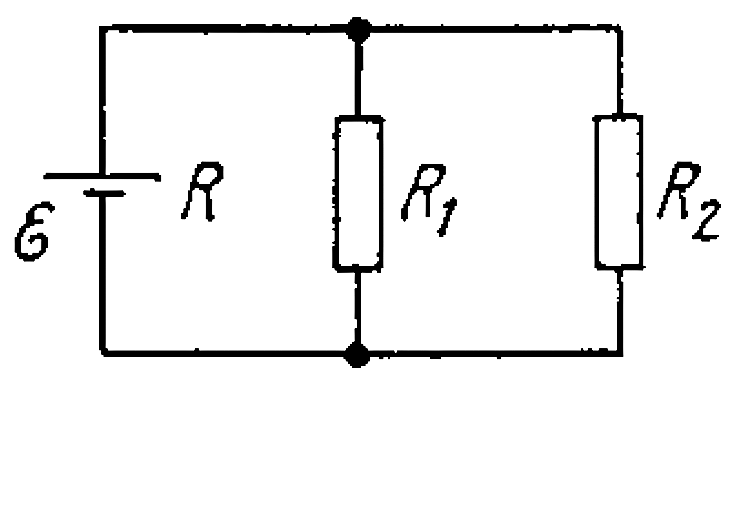
View SolutionIn the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.

View SolutionCalculate the resistivity (in Ωm) of a p type semiconductor if the density of holes is 1014cm−3and their mobility is 450cm2V−1s−1.(As the semiconductor is p-type, contribution of electrons can be ignored)
View SolutionA vertical shaft of light from a projector forms a light spot S=100cm2 in area on the celling of a round room of radius R=2.0m. The illuminance of the spot is equal to E=10001x. The reflection coeffiecient of the celling is equal to ρ=0.80. find the maximum illuminance of the well produced by the light reflected from the celling. the reflection is assumed to obey Lambert's law.
View SolutionAn intrinsic semiconductor has a resistivity of 0.50 Ω m at room temperature. Find the intrinsic carrier concentration if the mobilities of electrons and holes are 0.39m2V−1s−1 and 0.11m2V−1s−1 respectively
View Solution
