The resultant loudness at a point P is n dB higher than the loudness of S1 which is one of the two identical sound sources S1 and S2 reaching at that point in phase. Find the value of n.
Loudness due to S1=I1=ka2 where a is the amplitude and loudness due to S1 and S2 both
I2=k(2a)2=4I1
n=10log10(4I1I1)=10log10(4)=10(0.6)=6
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Comprehension144videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
The resultant loudness at a point P is n dB higher than the loudness of S1 whoch is one of the two identical sound sources S1 and S2 reaching at that point in phase. Find the value of n.
View SolutionSound level /loudness at any point in a room is increased from "50dB" to "60dB" by increasing the pressure amplitude, if final pressure amplitude is "K" times that of initial. Find the value of (K^(2))/(5)
View Solution
Knowledge Check
- Question 1 - Select One
Two identical sound S1 and S2 reach at a point P is phase. The resultant loudness at point P is n dB higher than the loudness of S1 the value of n is :
A2B4C5D6 - Question 2 - Select One
Which one of the two lodine atoms will be more reactive in the SN1 and SN2 reaction ?
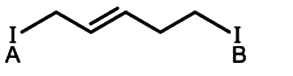 AA will be faster in SN1 reaction but slower in SN2BA will be faster both in SN1 and SN2 reactionCA and B will be equally reactive.DB will be faster in both SN1 and SN2 reaction
AA will be faster in SN1 reaction but slower in SN2BA will be faster both in SN1 and SN2 reactionCA and B will be equally reactive.DB will be faster in both SN1 and SN2 reaction - Question 3 - Select One
Two identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
A2B4C5D6
In Fig. , two point sources S1 and S2 which are in phase and separated by distance D=1.5λ , emit identical sound waves of wavelength λ.
(a) What is the path length difference of the waves from S1 and S2 at point P1, which lies on the perpendicular bisector of distance D, at a distance greater than D from the sources ? (That is, what is the difference in the distance from source S1 to point P1 and the distance from source S2 to P1?) What type of interference occurs at P1 ?
(b) What are the path length difference and type of interference at point P2 in fig.
(c ) Figure shows a circle with a radius much greater than D, centered on the midpoint between sources S1 and S2. What is the number of points N around this circle at which the interference is fully constructive? (That is, at how many points do the waves arrive exactly in phase?)View SolutionIn the shown fig. S1 and S2 are two identical coher- ent sources of sound, separated by a distance d. A receiver moves along the line XY (which is parallel to line S1 S2) to detect the intensity of sound at various points on the line. Distance of line XY from line S1 S2 isD(>>d). Point O is the foot of perpendicular bisector of the line S1 S2 on XY. Distance of first intensity maxima (on line XY) measured from O is y. Find percentage change in value of y if the temperature of air increases by 1%.
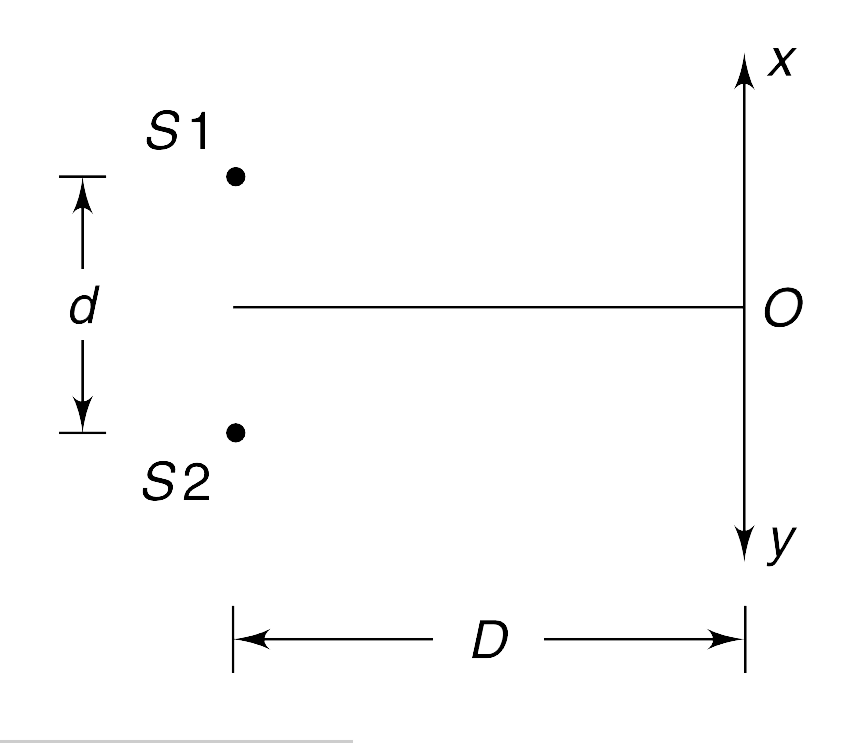 View Solution
View SolutionTwo sound sources oscillate in phase with a frequency of 100 Hz. At a point 1.74 m from one source and 1.16 m from the other, the amplitudes of sound from the two sources are A and 2 A respectively. Calculate the amplitude of the resultant disturbance at the point. [Speed of sound in air is v=348ms–1]
View SolutionTwo sources of sound S1andS2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0 . (a) If theta equals 45∘, what will be the intensity of sound detected at this point if one of the sources is switched off ? (b) What will be the answer of the previous part if θ=60∘ ?
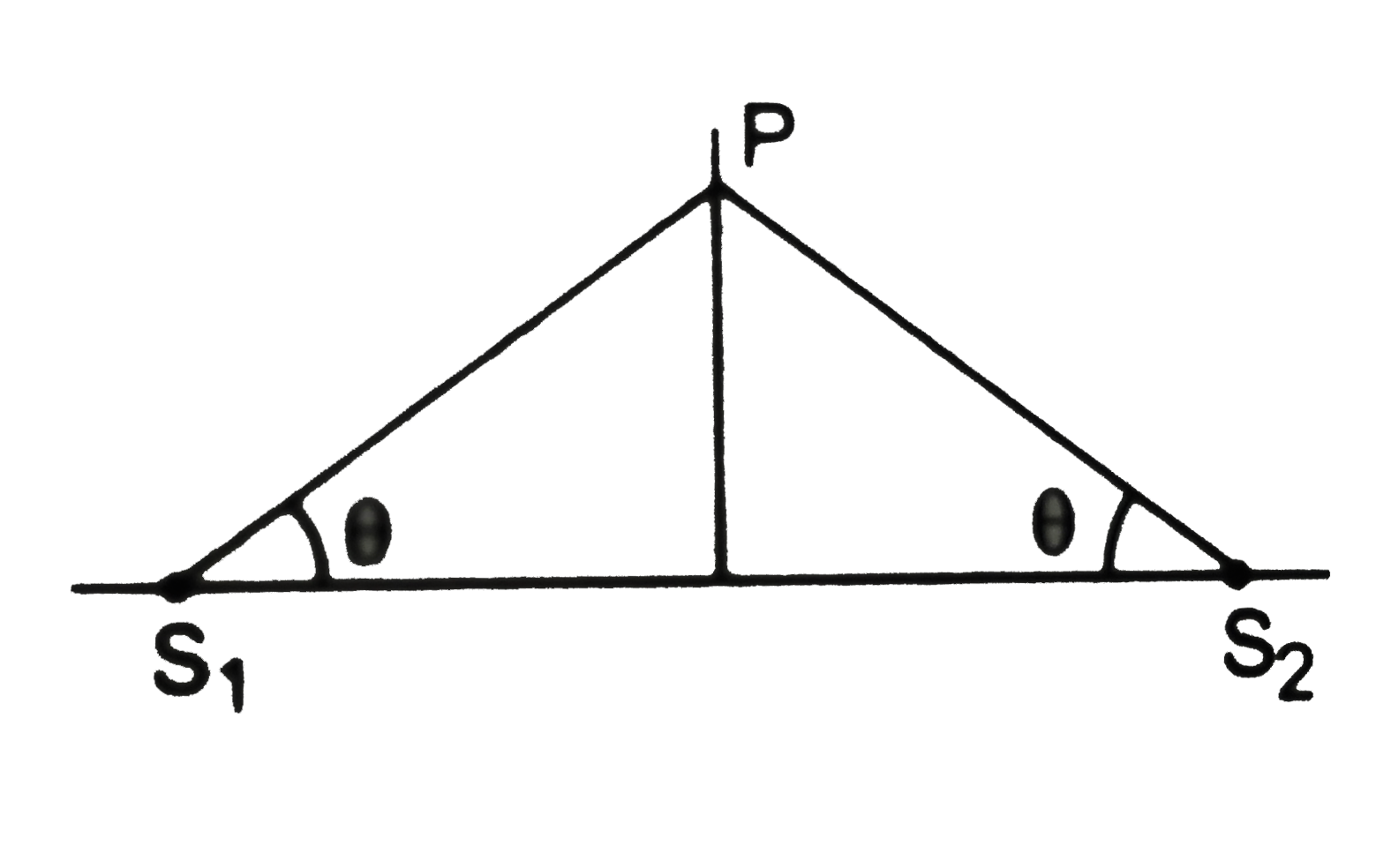 View Solution
View SolutionWhen beats are produced by two progressive waves of same amplitude and of nearly same frequencies then the maximum loudness of the resulting sound is n times the loudness of each of the component wave trains. The value of n is
View Solution

