Question

The resultant of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is perpendicular to the vector $\overrightarrow{A}$ and its magnitude is equal to half of the magnitude of the vector $\overrightarrow{B}$. Find out the angles between $\overrightarrow{A}$ and $\overrightarrow{B}$.
.

Explanation

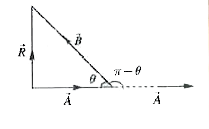
Since `vecR` is perpendicular to `vecA`. figure shows the three vectors `vecA, vecB and vec`R.
angle between `vecA and vecB` is p-q
`"sin" q=(R)/(B)=(B)/(2B)=(1)/(2)`
`rArr q=30^(@) rArr` angle between A and B is `150^(@)`