The simple 2Kg pendulum is released from rest in the horizontal position. As it reaches the bottom position, the cord wraps around the smooth fixed pin aat B and continues in the smaller arc in the vertical plane. Calculate the magnitude of the force R supported by the pin at B when the pendulum passes the position θ=30∘,(g=9.8m/s2)
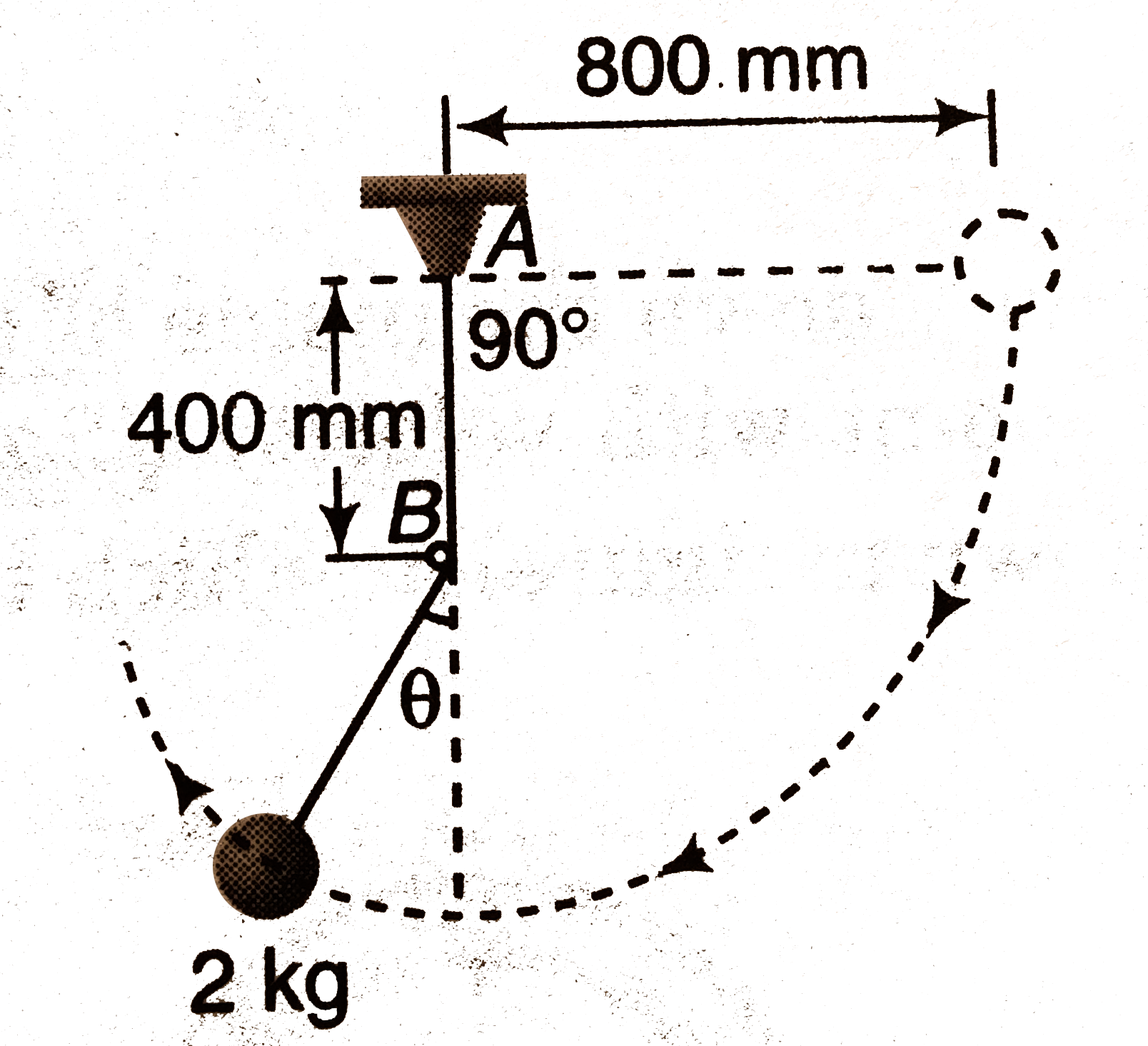
The correct Answer is:D
Speed of bob in the given position,
v=√2gh
Here, h=(400+400cos30∘)mm
=746mm=0.746m
:. v=√2×9.8×0.746=3.82m/s

Now T−mgcosθ=mv2r
T=2×9.8×cos30∘+2×(3.82)2(0.4)
or T=90N
:. R=Tsin30∘=45N
T'=Tcos30∘
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
The collar A is free to slide along the smooth shaft B mounted in the frame. The plane of the frame is the vertical . Determine the horizontal acceleration a of the frame necessary to maintain the collar in a fixed position on the shaft. (g=9.8m/s2)

View SolutionA wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View Solution
Knowledge Check
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
Aπ4Bcos−1(1√3)Csin−1(1√3)Dπ3A simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–
 Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2
Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2The bob of a 0.2 m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is
AgBg2C√3g2Dg4
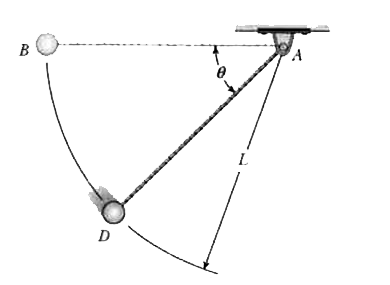
The pendulum bob B of mass M is released from rest when θ=0∘. Determine the intitial tension in the cord and also at the instant the bob reaches point D,θ=θ1. Neglect the size of the bob. Give M=3kg,θ1=45∘,L=2m,g=9.81m/s2.
View SolutionTwo small balls of equal mass are joined by a light rigid rod. If they are released from rest in the position shown and slide on the smooth track in the vertical plane, the speed of balls when A reaches B's position and B is at B is r=0.25m B
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View SolutionThe bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance.
(Take g=10ms−2)
View SolutionTwo identical pendulums A an dB are suspended from the same point. Both are givne positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles θ1 and θ2 with the vertical respectively.
View Solution
