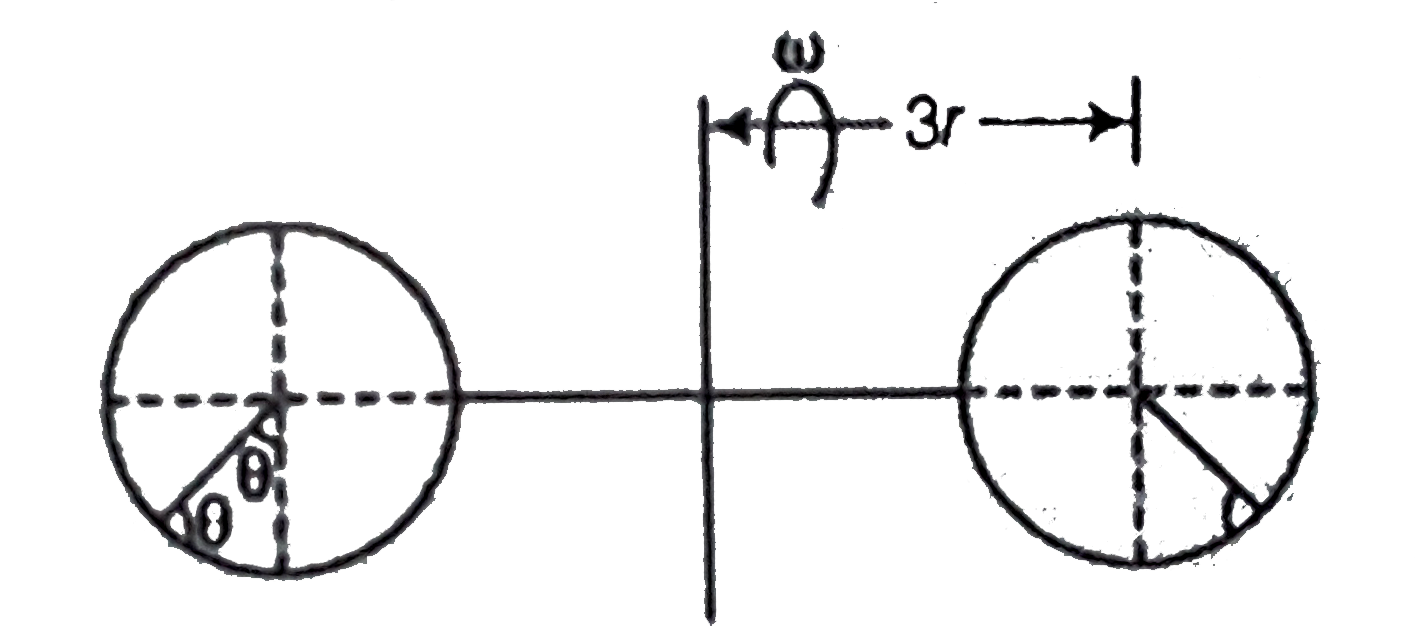
The small sphericla balls are free to move on the inner surface of the rotating spherical chamber of radius R=0.2m If the balls reach a steady at angular position θ=45∘, the anglular speed ω of devices is
8rad/s
2rad/s
3.64rad/s
9.34rad/s
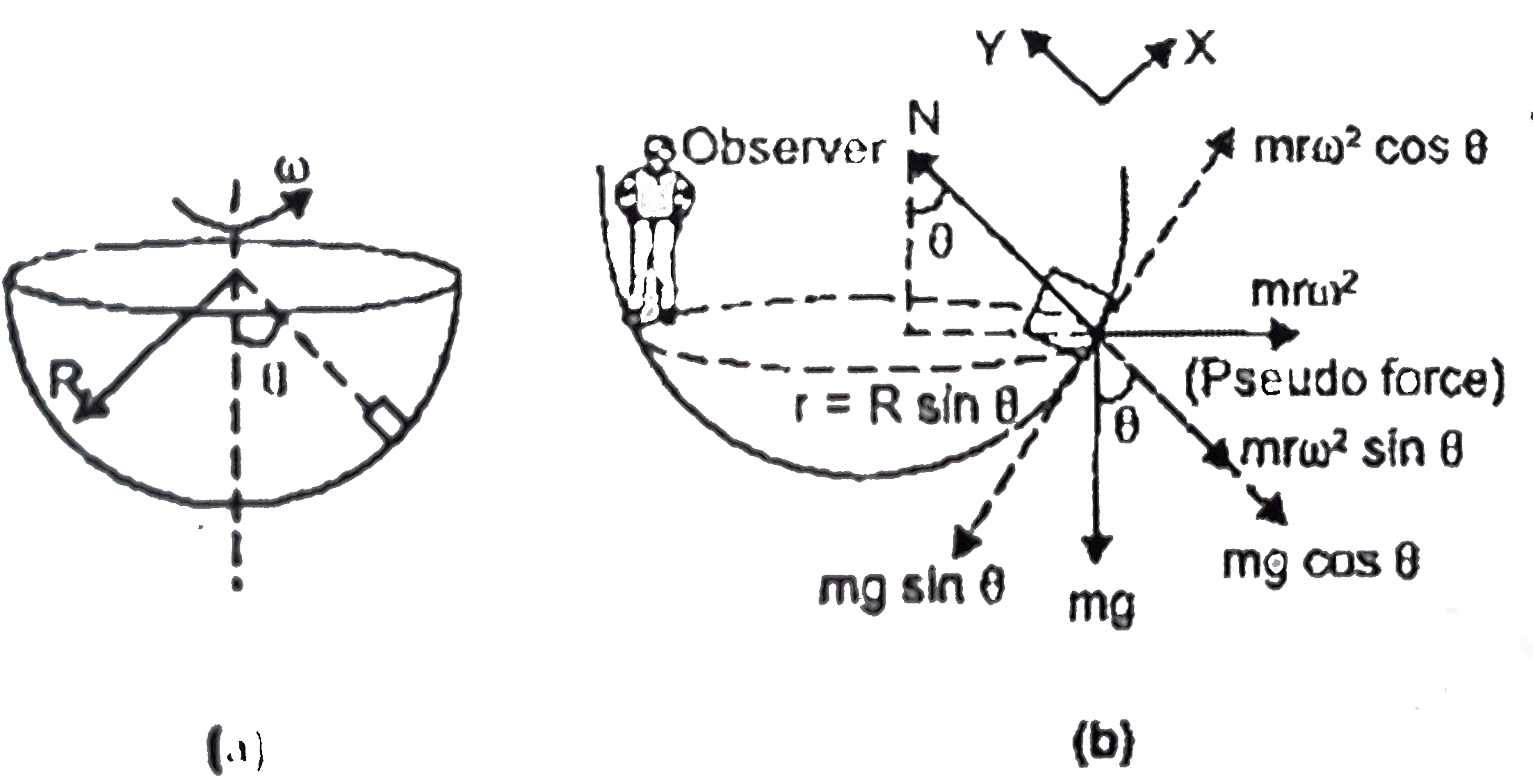
(c) Here, R=0.2m
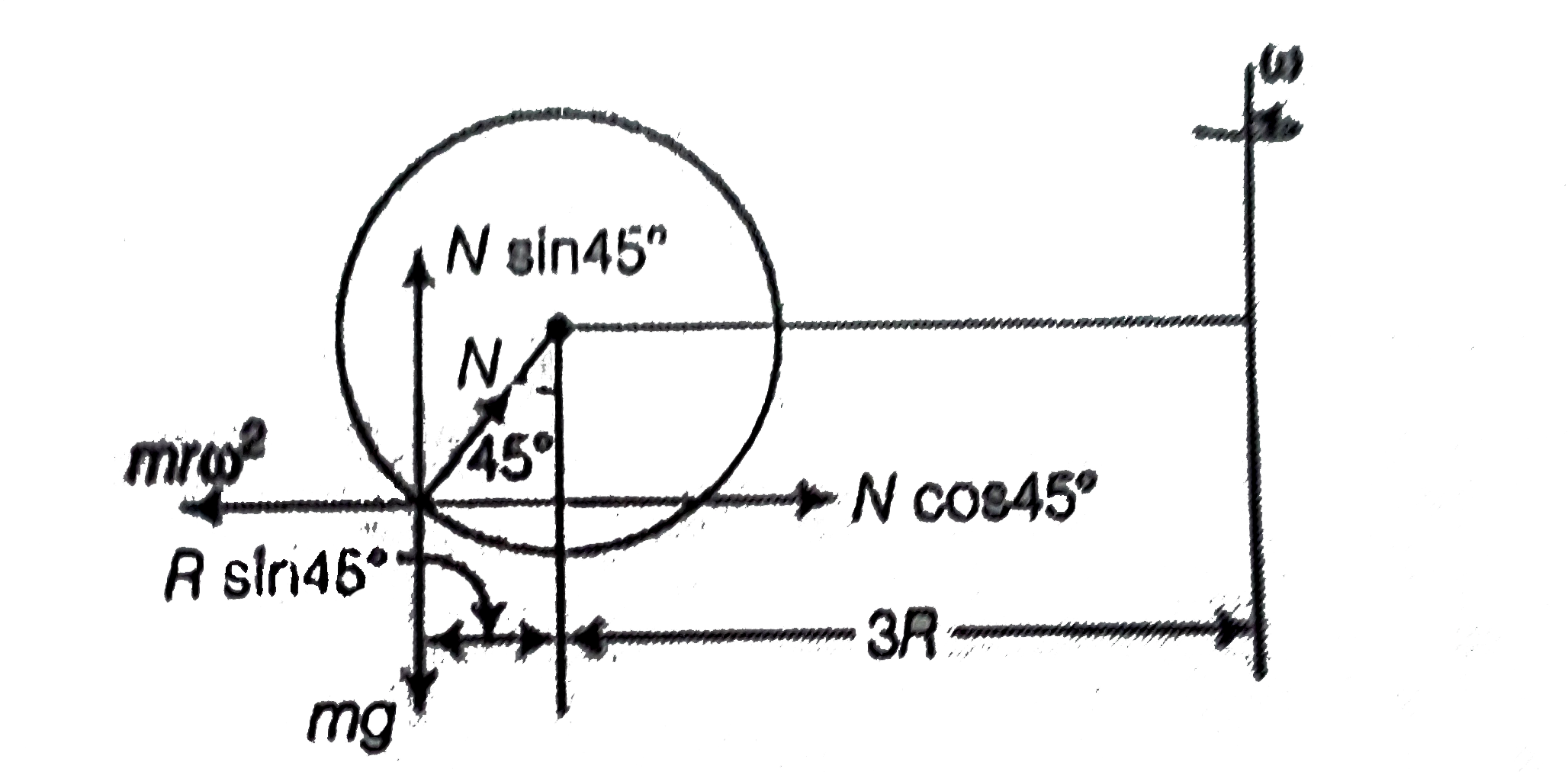
From figure r=3R+Rsin45∘
In the fram of rotating spherical chamber (n0n-inertial)
Ncos45∘=mrω2
Nsin45∘−mg
Dividing Eq. (ii) by Eq(i), we get
∴ tan45∘=mgmrω2=grω2
∴ ω=√gr=
⎷⎛⎜⎝g3R+R√2⎞⎟⎠=3.64rad/s
Topper's Solved these Questions
Similar Questions
A small insect is climbing slowly along the inner wall of a hemispherical bowl of radius R. The insect is unable to climb beyond θ=45∘. Whenever it tries to climb beyond θ=45∘, it slips.
(a) Find the minimum angular speed ω with which the bowl shall be rotated about its vertical radius so that the insect can climb upto θ=60∘.
(b) Find minimum ω for which the insect can move out of the bowl.

View SolutionA package of mass m is placed inside a drum that rotates in the vertical plane at the constant angular speed ω=1.36 rad/s. If the package reaches the position θ=45∘ before slipping determine the coefficient of friction between the package and drum. See fig.
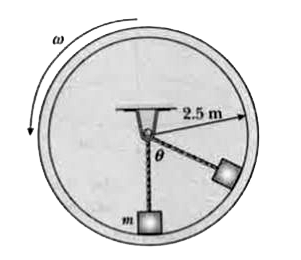
View Solution
Knowledge Check
A small spherical steel ball is placed a little away from the centre of a large concave mirror of radius of curvature 2.5 m, if the ball is released, then the period of the motion will be (g=10m/s2)
Aπ/4sBπ/2sCπ/sD2πsA disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity ω0 and released. The angular speed of the disc when the balls reach the end of the disc is -
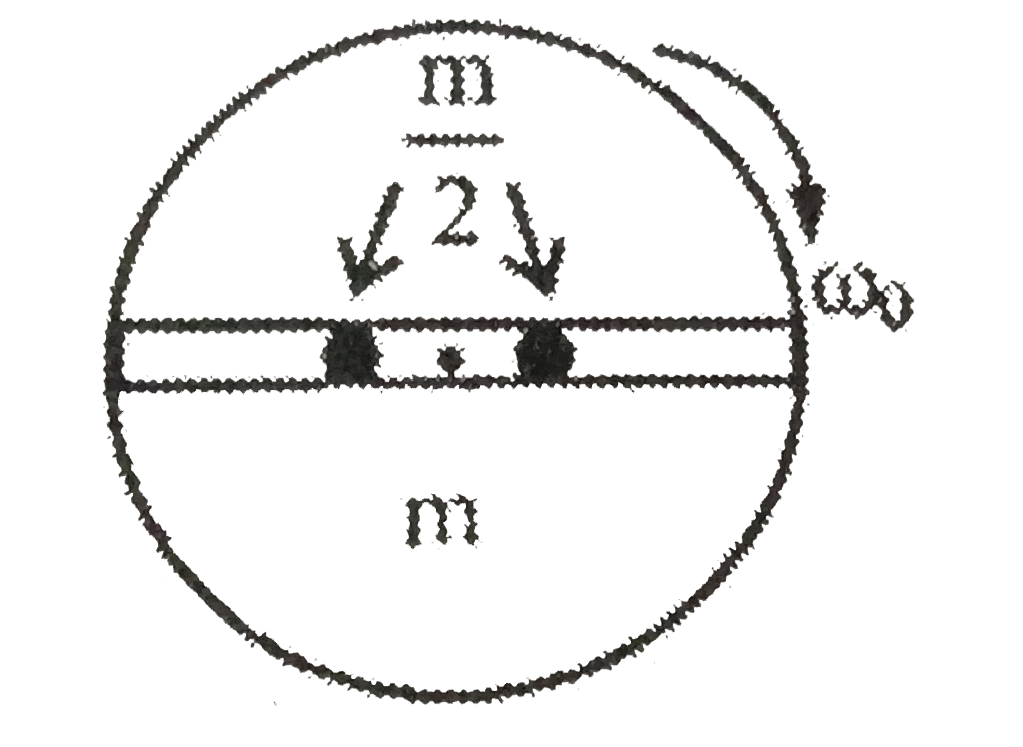 Aω02Bω03C2ω03Dω04
Aω02Bω03C2ω03Dω04A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc isAω02Bω03C2ω03Dω04
A small ball of mass m is released from rest from the position shown . All contact surface are smooth . The speed of the ball when it reaches its lowest position is
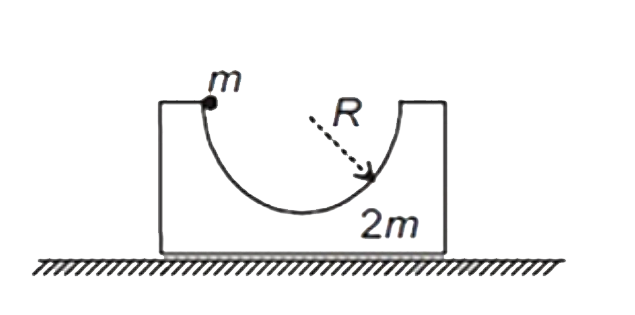
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA person stands in contact against the inner surface of a cylindrical drum of radius (R ) rotating with angular velocity ω . The coefficient of friction between the inner surface of the minumum rotational speed of the cylinder , which enables the person to ramain stuck to the wall , when the platform on which the person was standing is suddenly removed ?
View Solution