The table records the mass and speed of an object travelling at constant velocity on a frictionless track, as performed by a student conducting a physics lab exercise. In her analysis, the student had to state the trial in which the object had the greatest momentum and the trial in which it had the greatest kinetic energy. which of the following gives the correct answer?
Greatest Momentum-Trial 1, Greatest Kinetic Energy-Trial 3
Greatest Momentum-Trial 2, Greatest Kinetic Energy-Trial 2
Greatest Momentum-Trial 3, Greatest Kinetic Energy-Trial 2
Greatest Momentum-Trial 4, Greatest Kinetic Energy-Trial 4
The correct Answer is:C
Since momentum, p, is equal to mv, we just multiply the two entries (m and v) in each row of the table and see which one is the greatest. This occurs in triel 3, where p=(2kg)(2m/s)=4kg.m/s. so, the answer must be either (C) or (D). To decided which, we only need to find the kinetic energy of the object in trial 2 and trial 3 and choose the one that's greater. since 12mv2=12(1kg)(3m/s)2=92J in trial 2, but only 12(2kg)(2m/s)2=4J is Trial 3, we seee that the object's kinetic energy is greater in trial 2, so the answer is (C).
Topper's Solved these Questions
Similar Questions
Two object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object has greatest terminal speed in the liquid ?
View Solution
Knowledge Check
Uniform cicular motion is used in physics to describe the motion of an object traveling at a constant speed in a circle. The speed of the object is called tangential velocity and it can be calculated using the formula abovce, where r is the radius of the circle and T is the time is takes for the object to make one complete circle, called a peroid. WHich of the following formulas could be used to find the length of one period if you know the tengential velocity and the radius of the circle ?
AT=v2πrBT=2πrvCT=2πrvDT=12πrvAcceleration versus time graph for four objects are shown below. All axes have the same scale. Which object had the greatest change in velocity during the interval ?
A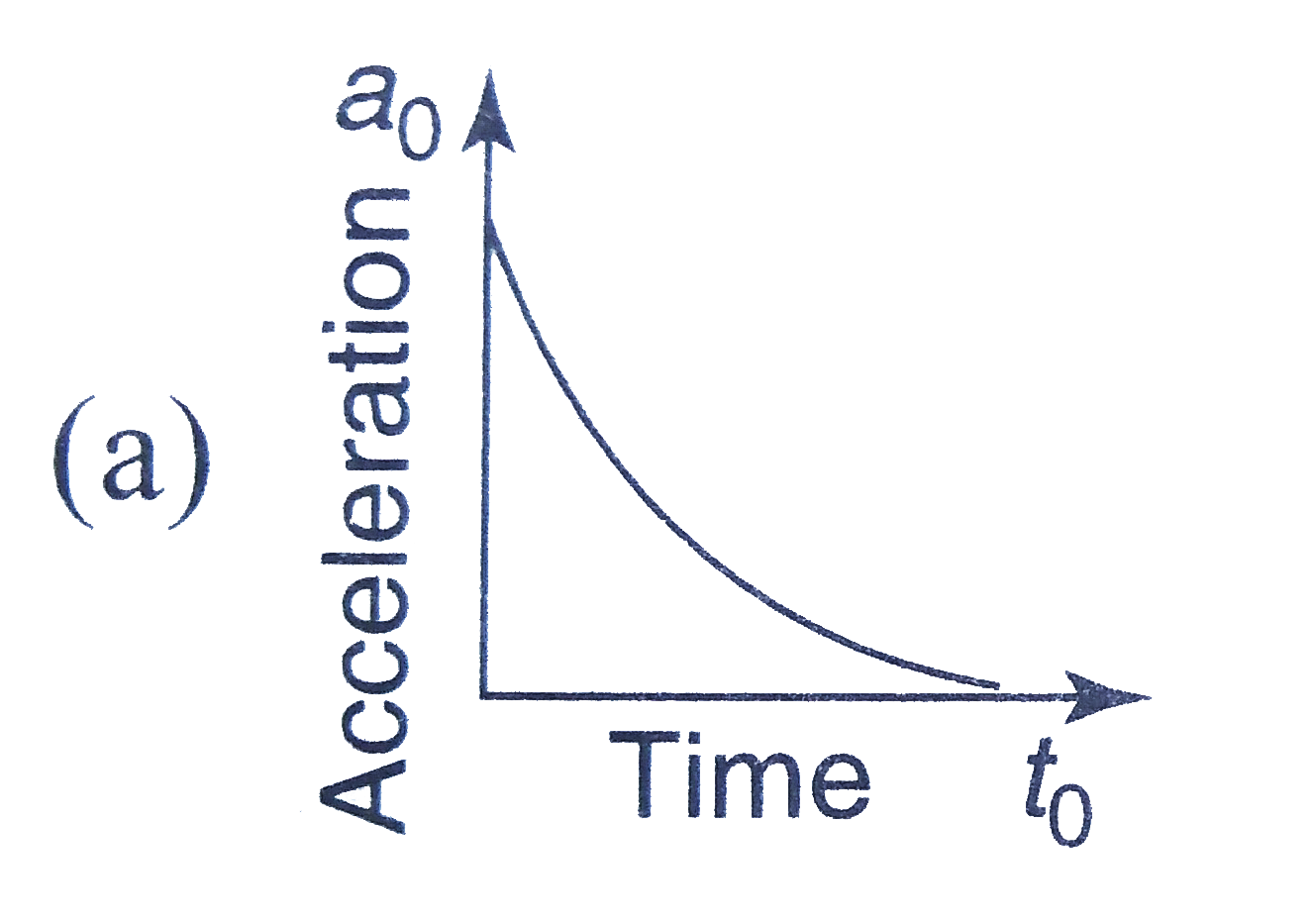 .B
.B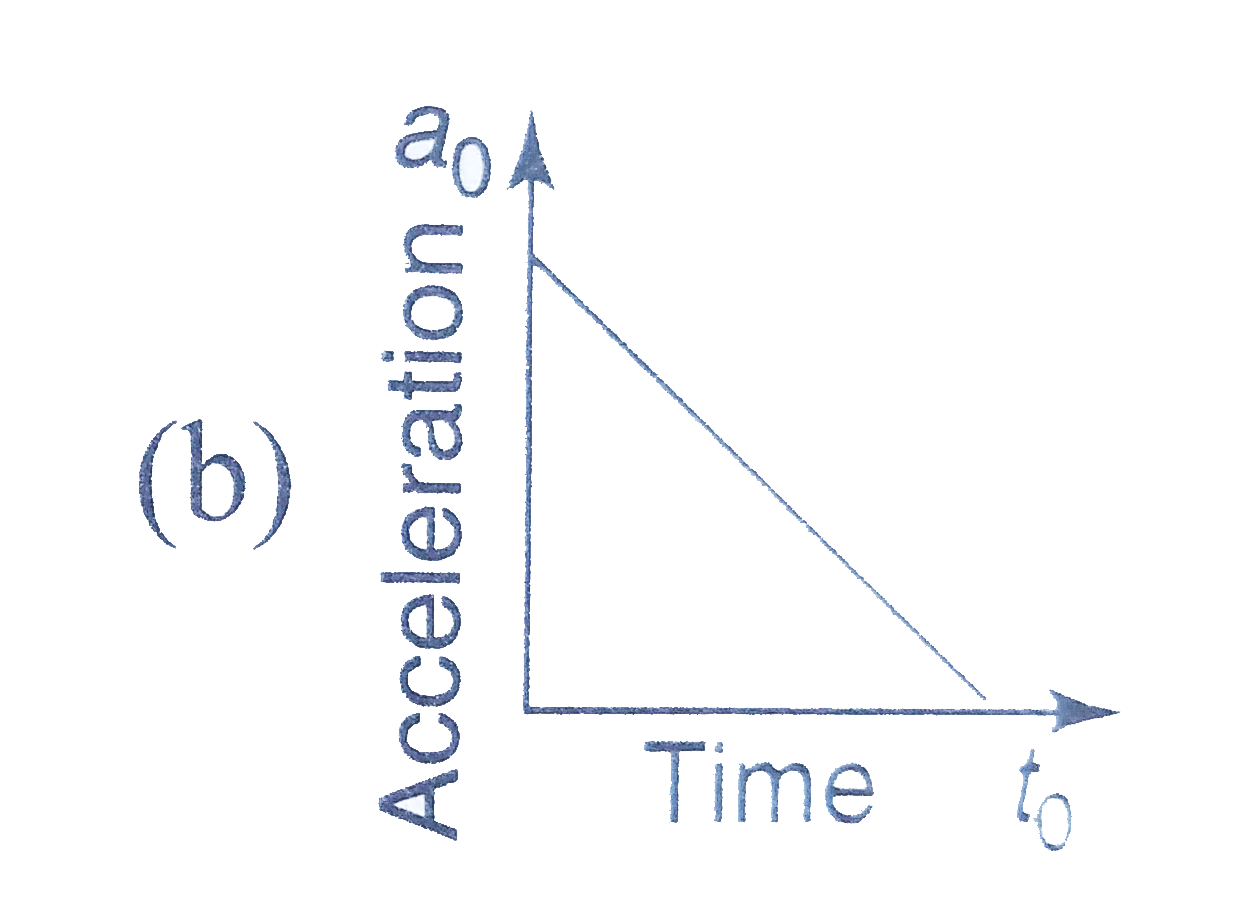 .C
.C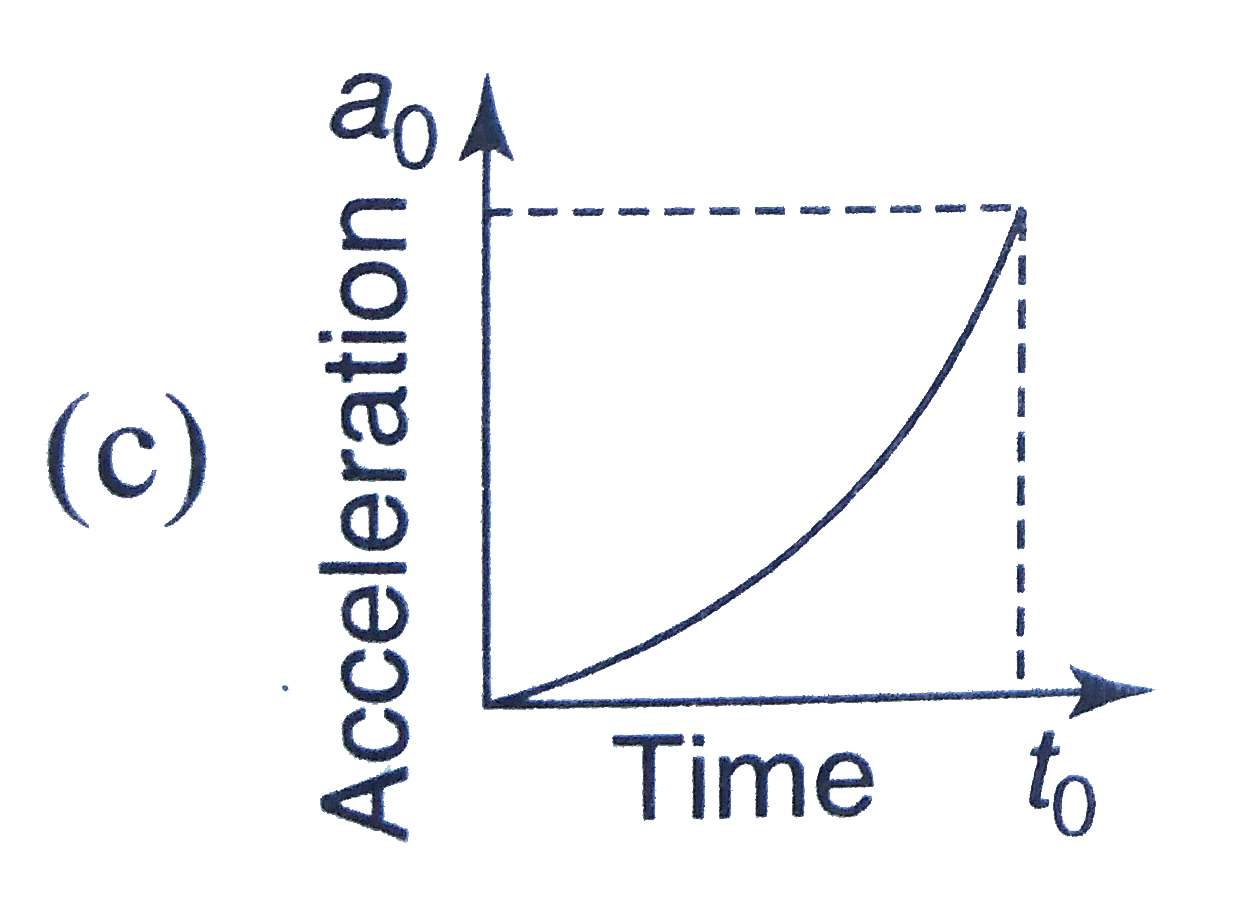 .D
.D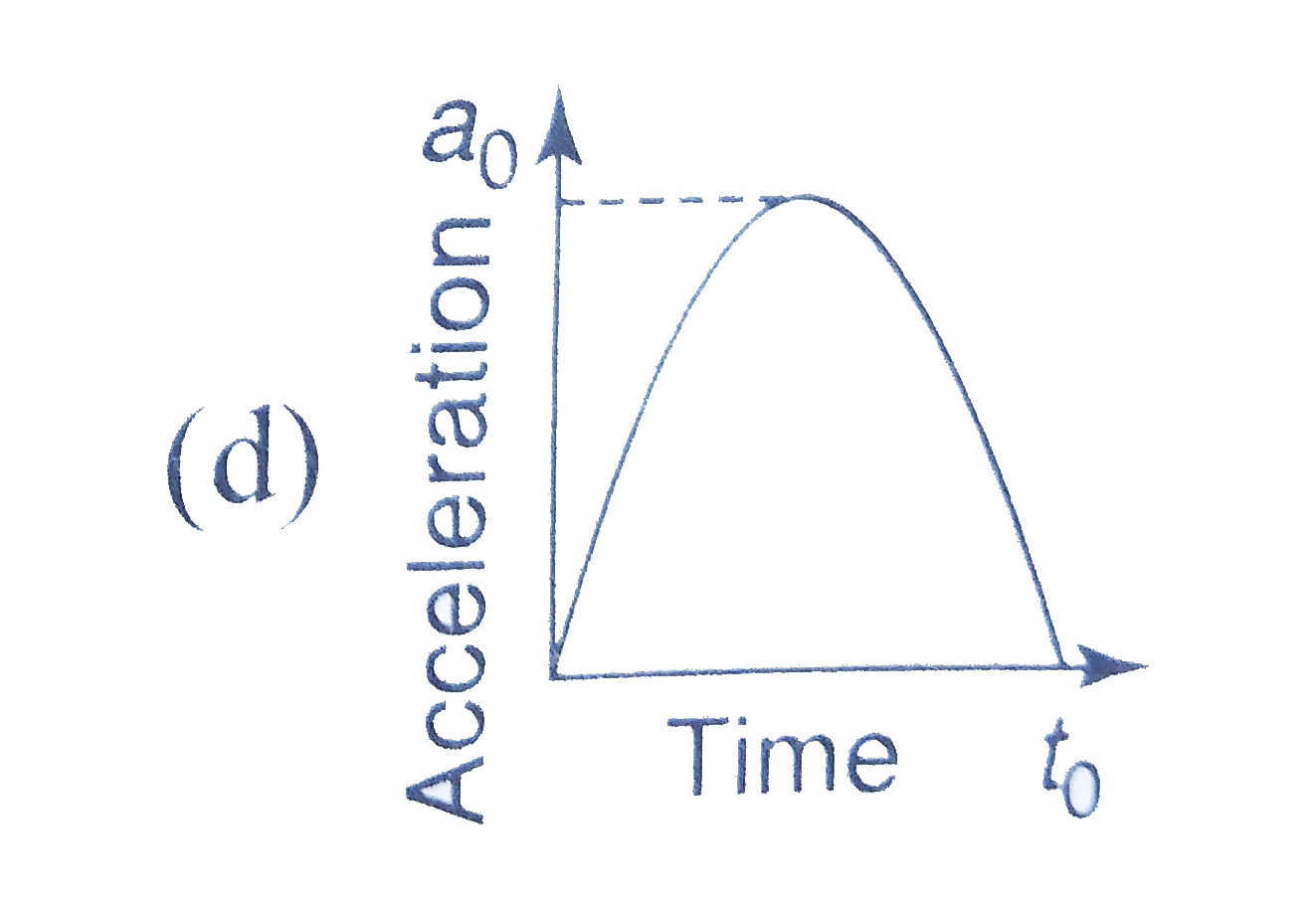 .
.Two object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
Ap1<p2Bp1>p2CK1>K2DK1<K2
A student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student performs another trial in which the ball is launched at speed 5.0m/s. Its range is approximately:
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object has greatest terminal speed in the liquid ?
View SolutionIn a survey of 25 students, it was found that 15 had taken Mathematics, 12 had taken Physics and 11 had taken Chemistry, 5 had taken Mathematics and Chemistry, 9 had taken Mathematics and Physics, 4 had taken Physics and Chemistry and 3 had taken all the three subjects.
Consider the following statements :
1. The number of students who had taken only one subject is equal to the number of students who had taken only two subjects.
2. The number of students who had taken at least two subjects is four times the number of students who had taken all the three subjects.
Which of the above statements is/are correct ?
View Solution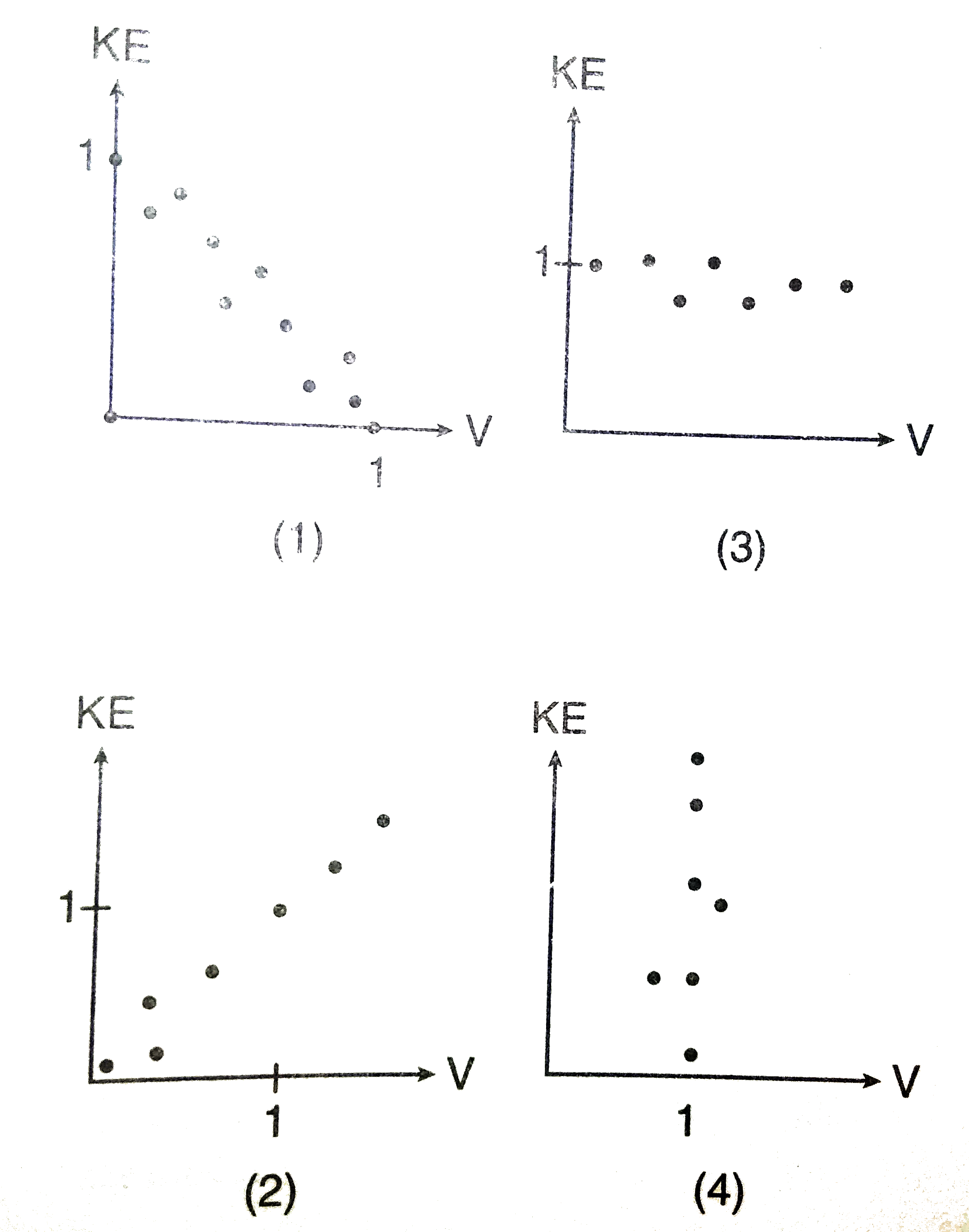
In the physics lab, a student determined the kinetic energy, KE, of an object at various velocities, V, and found a strong positive association between KE and V. Which of the above scatterplots show this relationship?
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
The student performs another trial in which the ball is launched at speed 5.0m/s. Its range is approximately:
View Solution
