The thermal powered density u is generated uniformly inside a uniform sphere of radius R and thermal conductivity Find the temperature distribution in the sphere when the steady state temperature at the surface is T0.
The correct Answer is:[T0+u(R2−r2)6k]
To find the temperature distribution in a uniform sphere with a uniform thermal power density U generated inside it, we can follow these steps:
Step 1: Understand the Problem
We have a uniform sphere of radius R and thermal conductivity k. Inside this sphere, there is a uniform thermal power density U. The steady-state temperature at the surface of the sphere is given as T0. We need to find the temperature distribution T(r) within the sphere.
Step 2: Set Up the Heat Equation
In a steady state, the heat generated inside the sphere must equal the heat conducted to the surface. The heat conduction can be described by Fourier's law:
dqdt=−kAdTdr
where A is the surface area of a sphere at radius r, which is 4πr2.
Step 3: Heat Generation Inside the Sphere
The heat generated inside the sphere can be expressed as:
dqdt=U⋅V
where V is the volume of the sphere of radius r, given by 43πr3.
Step 4: Equate Heat Generation and Heat Conduction
Setting the two expressions for heat equal gives:
−k⋅4πr2dTdr=U⋅43πr3
Step 5: Simplify the Equation
We can simplify this equation by canceling 4π from both sides:
−kr2dTdr=U3r3
Rearranging gives:
dTdr=−U3kr
Step 6: Integrate the Equation
Integrating both sides with respect to r:
∫dT=−U3k∫rdr
This results in:
T=−U6kr2+C
where C is the constant of integration.
Step 7: Apply Boundary Conditions
We know that at the surface of the sphere (where r=R), the temperature T(R)=T0:
T0=−U6kR2+C
Solving for C:
C=T0+U6kR2
Step 8: Write the Final Temperature Distribution
Substituting C back into the equation for T:
T(r)=−U6kr2+T0+U6kR2
This simplifies to:
T(r)=T0+U6k(R2−r2)
Final Answer
The temperature distribution in the sphere is given by:
T(r)=T0+U6k(R2−r2)
We have a uniform sphere of radius R and thermal conductivity k. Inside this sphere, there is a uniform thermal power density U. The steady-state temperature at the surface of the sphere is given as T0. We need to find the temperature distribution T(r) within the sphere.
In a steady state, the heat generated inside the sphere must equal the heat conducted to the surface. The heat conduction can be described by Fourier's law:
The heat generated inside the sphere can be expressed as:
Setting the two expressions for heat equal gives:
We can simplify this equation by canceling 4π from both sides:
Integrating both sides with respect to r:
We know that at the surface of the sphere (where r=R), the temperature T(R)=T0:
Substituting C back into the equation for T:
The temperature distribution in the sphere is given by:
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct
20 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
The thermal power of density ω is generated uniformly inside a uniform sphere of radius R and heat conductivity coefficient x. Find the temperature distribution in the sphere provided the steady-state temperature at its surface is eqal to T0.
View SolutionThermal power of density W is generated uniformly inside a sphere of radius R and thermal conductivity λ. Find the temperature distribution along the radius of the sphere in the steady state of it when its outer surface is at temperature T0.
View Solution
Knowledge Check
The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
Aheat flows in the rod from high temperature to low temperature even if the rod has nonuniform cross sectional area.Btemperature gradient along length is same even if the rod has non uniform cross sectional area.Cheat current is same even if the rod has nono-uniform cross sectional areaDif the rod has uniform cross sectional area the temperature is same at all points of the rod.Three rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
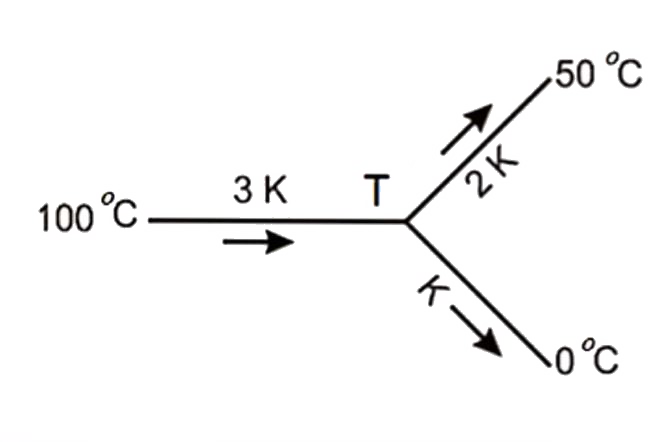A2003∘cB1003∘cC75∘cD503∘c
The thermal power of density 100J/m^(3) is generated at a constant rate inside a uniform sphere of radius 10m and thermal conductivity 0.25wm−1k−1 .The temperature inside the sphere at a distance "5m" from center will be, if steady state temperature at surface is 600k
View SolutionA constant electric current flows along a uniform wire with cross-sectional radius R and heat conductivity coefficient x. A unit volume of the wire generates a thermal power ω. Find the temperature distribution across the wire provided the steady-state temperature at the wire surface is equal to T0.
View SolutionA constant current flows along a wire of radius R and heat conductivity coefficient λ. Heat is produced in unit volume of the wire at a constant rate W. Find the temperature distribution along the radius in the steady state, when the constant temperature of the surface of the wire is T0.
View SolutionHeat is generated uniformly per unit volume inside a spherical volume of radius 1 m and thermal conductivity 16 W/mK at rate of 20W/m3. What is the temperature (in ∘C) of center of sphere if the outer surface temperature of the sphere is 20∘C?
View SolutionA charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionWhat do you mean by variable state and steady state in thermal conduction ? Define temperature gradient
View Solution