The time taken by a simple pendulum to perform 100 vibration is 8 minutes 9 sec in bombay and 8 minutes 20 sec. in pune. Calcualte the ratio of acceleration due to gravity in bombay and pune.
The correct Answer is:1.0455
To solve the problem, we need to use the formula for the time period of a simple pendulum, which is given by:
T=2π√Lg
where:
- T is the time period of the pendulum,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
1. Convert the time taken for vibrations into seconds:
- For Bombay:
- 8 minutes 9 seconds = 8×60+9=489 seconds.
- For Pune:
- 8 minutes 20 seconds = 8×60+20=500 seconds.
2. Calculate the time period for one vibration:
- For Bombay:
- Time period TB=489 seconds100=4.89 seconds.
- For Pune:
- Time period TP=500 seconds100=5.00 seconds.
3. Set up the ratio of the time periods:
- The ratio of the time periods is given by:
TBTP=4.895.00
4. Use the time period formula to express g:
- From the formula T=2π√Lg, we can express g as:
g=4π2LT2
- Therefore, for Bombay and Pune:
gB=4π2LT2B
gP=4π2LT2P
5. Calculate the ratio of gB and gP:
- The ratio of the accelerations due to gravity is:
gBgP=T2PT2B
- Substituting the values of TB and TP:
gBgP=(5.00)2(4.89)2
gBgP=25.0023.9121≈1.04
6. Final ratio of acceleration due to gravity:
- Thus, the ratio of acceleration due to gravity in Bombay and Pune is approximately:
gBgP≈1.04
Final Answer:
The ratio of acceleration due to gravity in Bombay and Pune is approximately 1.04:1.
- T is the time period of the pendulum,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
- For Bombay:
- 8 minutes 9 seconds = 8×60+9=489 seconds.
- For Pune:
- 8 minutes 20 seconds = 8×60+20=500 seconds.
- For Bombay:
- Time period TB=489 seconds100=4.89 seconds.
- For Pune:
- Time period TP=500 seconds100=5.00 seconds.
- The ratio of the time periods is given by:
TBTP=4.895.00
- From the formula T=2π√Lg, we can express g as:
g=4π2LT2
- Therefore, for Bombay and Pune:
gB=4π2LT2B
gP=4π2LT2P
- The ratio of the accelerations due to gravity is:
gBgP=T2PT2B
- Substituting the values of TB and TP:
gBgP=(5.00)2(4.89)2
gBgP=25.0023.9121≈1.04
- Thus, the ratio of acceleration due to gravity in Bombay and Pune is approximately:
gBgP≈1.04
The ratio of acceleration due to gravity in Bombay and Pune is approximately 1.04:1.
Topper's Solved these Questions
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise
233 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Problem
23 Videos
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66 Videos
- Physical worldBOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise
49 Videos
Similar Questions
The acceleration due to gravity on the surface of earth is 9.8ms−2.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint :Te=2π√LgeTm=2π√Lgm
T2eT2m=gmge
gm=T2eT2mge
View SolutionA simple pendulum makes 20 oscillations in one second on the surface of the earth. Determine the time period of the simple pendulum on the surface of a planet where the acceleration due to gravity is one fourth of the acceleration due to gravity on the surface of the earth .
View Solution
Knowledge Check
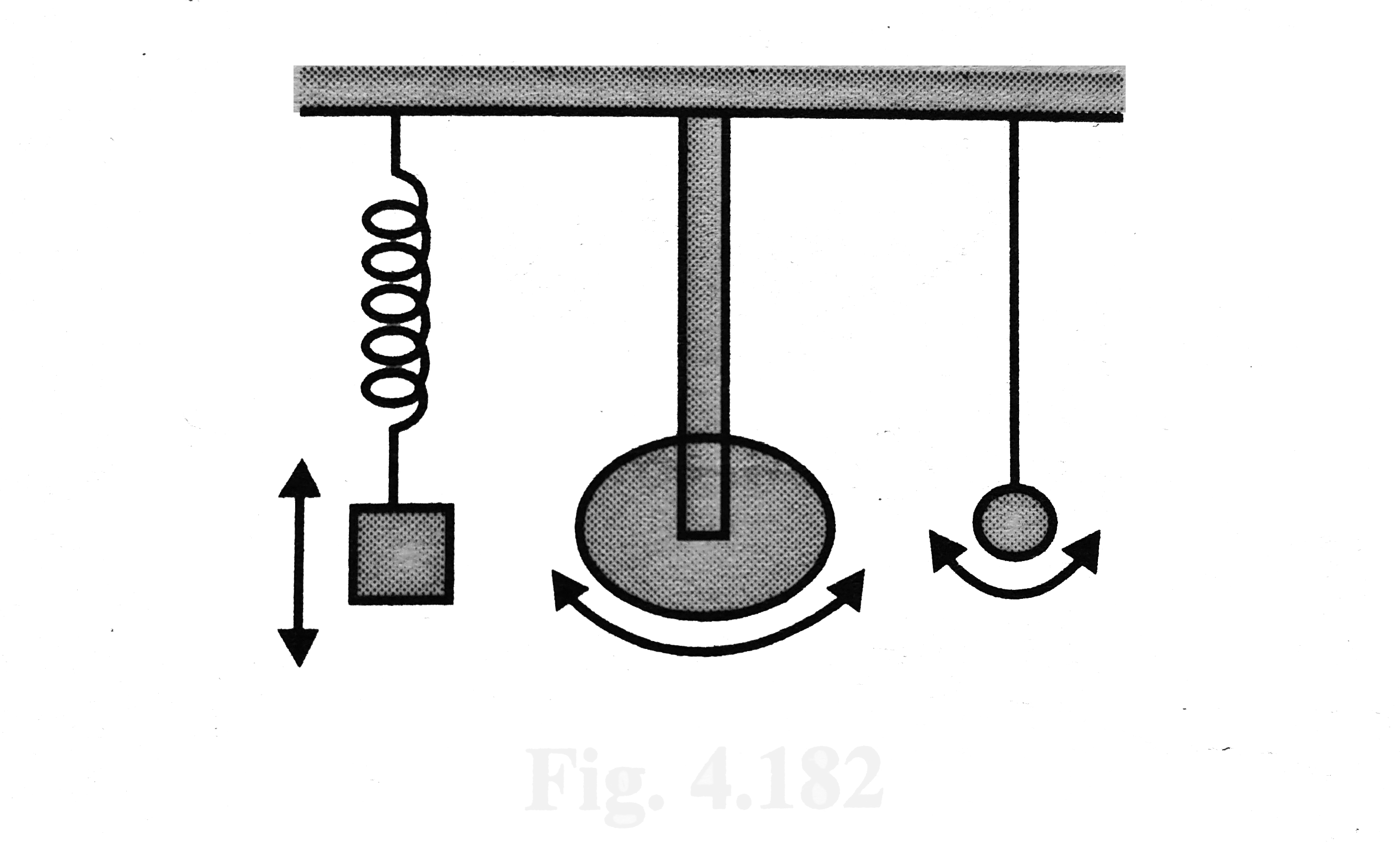
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.AStatement I is true statement II is true, Statement II is a correct explanation for Statement I.BStatement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.CStatement I is true, Statement II is falseDStatement I is false, Statement II is trueA simple pendulum undergoes 20 oscillation's in 30 seconds. What is the percentage error in the value of acceleration due to gravity provided length of pendulum is 55cm, least count of rmeasurement of time and length are 1s and 1mm respectively
A3.4%B6.8%C5.5%D11%
A simple pendulum makes 20 oscillations in one second on the surface of the earth. Determine the time period of the simple pendulum on the surface of a planet where the acceleration due to gravity is one fourth of the acceleration due to gravity on the surface of the earth .
View SolutionThe time period of a pendulum on the surfacce of the moon is 5s. If it is a seconds pendulum on earth and the acceleratio due to gravity on the earth is 9.8ms−2, find the acceleration due to gravity on the surface of the moon.
View SolutionIf the length of a seconds pendulum on a planet is 2 m then the acceleration due to gravity on the surface of that planet is ______ (Take the acceleration due to gravity on the surface of the Earth =9.8 ms−2)
View SolutionThe time periods of two simple pendula having different length is the same on two different planets .if the lengths of the two pendula are in ratio of 1:9, then the ratio of the accelerations due to gravity on the two planets is ______
View SolutionGiven that the mass of the earth is 81.5 times the mass of the moon and the diameter of the moon is 0.27 times that of the earth . Calculate the value of acceleration due to gravity at the surface of the moon . Given 'g' on the earth = 9.8ms−2
View SolutionAn artificial satellite is revolving in a circular orbit at a height of 600 km from the earth's surface. If its time of revolution be 100 minutes, calculate the acceleration due to gravity acting on it towards the earth. Radius of earth =6.4×106 m
View Solution
