Draw displacement-time, velocity-time and acceleration-time graphs for a particle executing simple harmonic motion. Discuss their phase relationship.
To solve the question of drawing displacement-time, velocity-time, and acceleration-time graphs for a particle executing simple harmonic motion (SHM) and discussing their phase relationships, we will follow these steps:
Step 1: Understand the equations of SHM
The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
where:
- A is the amplitude,
- ω is the angular frequency,
- t is time.
Step 2: Draw the Displacement-Time Graph
The displacement-time graph is a sine wave. The graph starts at the origin (0,0) when t=0, reaches the maximum amplitude A at t=T4, returns to 0 at t=T2, reaches the minimum amplitude −A at t=3T4, and returns to 0 at t=T (where T is the time period).
Graph Characteristics:
- The graph oscillates between A and −A.
- It is periodic with a period T.
Step 3: Find the Velocity Equation
The velocity v is the derivative of displacement with respect to time:
v(t)=dxdt=ddt(Asin(ωt))=Aωcos(ωt)
Step 4: Draw the Velocity-Time Graph
The velocity-time graph is a cosine wave. It starts at its maximum value Aω when t=0, crosses zero at t=T4, reaches its minimum −Aω at t=T2, crosses back to zero at t=3T4, and returns to maximum Aω at t=T.
Graph Characteristics:
- The graph oscillates between Aω and −Aω.
- It is also periodic with a period T.
Step 5: Find the Acceleration Equation
The acceleration a is the derivative of velocity with respect to time:
a(t)=dvdt=ddt(Aωcos(ωt))=−Aω2sin(ωt)
Step 6: Draw the Acceleration-Time Graph
The acceleration-time graph is a sine wave but inverted. It starts at 0 when t=0, reaches its maximum −Aω2 at t=T4, returns to 0 at t=T2, reaches its minimum Aω2 at t=3T4, and returns to 0 at t=T.
Graph Characteristics:
- The graph oscillates between −Aω2 and Aω2.
- It is periodic with a period T.
Step 7: Discuss the Phase Relationships
1. Displacement and Velocity: The phase difference between displacement and velocity is π2 (90 degrees). This means that when displacement is at its maximum, velocity is zero.
2. Velocity and Acceleration: The phase difference between velocity and acceleration is also π2. This indicates that when velocity is at its maximum, acceleration is zero.
3. Displacement and Acceleration: The phase difference between displacement and acceleration is π (180 degrees). This means that when displacement is at its maximum, acceleration is at its minimum (negative maximum).
Summary of Graphs
- Displacement-Time Graph: Sine wave starting from (0,0).
- Velocity-Time Graph: Cosine wave starting from maximum.
- Acceleration-Time Graph: Inverted sine wave starting from (0,0).
The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt)
where:
- A is the amplitude,
- ω is the angular frequency,
- t is time.
The displacement-time graph is a sine wave. The graph starts at the origin (0,0) when t=0, reaches the maximum amplitude A at t=T4, returns to 0 at t=T2, reaches the minimum amplitude −A at t=3T4, and returns to 0 at t=T (where T is the time period).
- The graph oscillates between A and −A.
- It is periodic with a period T.
The velocity v is the derivative of displacement with respect to time:
v(t)=dxdt=ddt(Asin(ωt))=Aωcos(ωt)
The velocity-time graph is a cosine wave. It starts at its maximum value Aω when t=0, crosses zero at t=T4, reaches its minimum −Aω at t=T2, crosses back to zero at t=3T4, and returns to maximum Aω at t=T.
- The graph oscillates between Aω and −Aω.
- It is also periodic with a period T.
The acceleration a is the derivative of velocity with respect to time:
a(t)=dvdt=ddt(Aωcos(ωt))=−Aω2sin(ωt)
The acceleration-time graph is a sine wave but inverted. It starts at 0 when t=0, reaches its maximum −Aω2 at t=T4, returns to 0 at t=T2, reaches its minimum Aω2 at t=3T4, and returns to 0 at t=T.
- The graph oscillates between −Aω2 and Aω2.
- It is periodic with a period T.
1. Displacement and Velocity: The phase difference between displacement and velocity is π2 (90 degrees). This means that when displacement is at its maximum, velocity is zero.
2. Velocity and Acceleration: The phase difference between velocity and acceleration is also π2. This indicates that when velocity is at its maximum, acceleration is zero.
- Displacement-Time Graph: Sine wave starting from (0,0).
- Velocity-Time Graph: Cosine wave starting from maximum.
- Acceleration-Time Graph: Inverted sine wave starting from (0,0).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2The phase of a particle executing simple harmonic motion is π2 when it has
AMaximum velocityBMaximum accelerationCMaximum energyDMaximum displacementIf a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3)
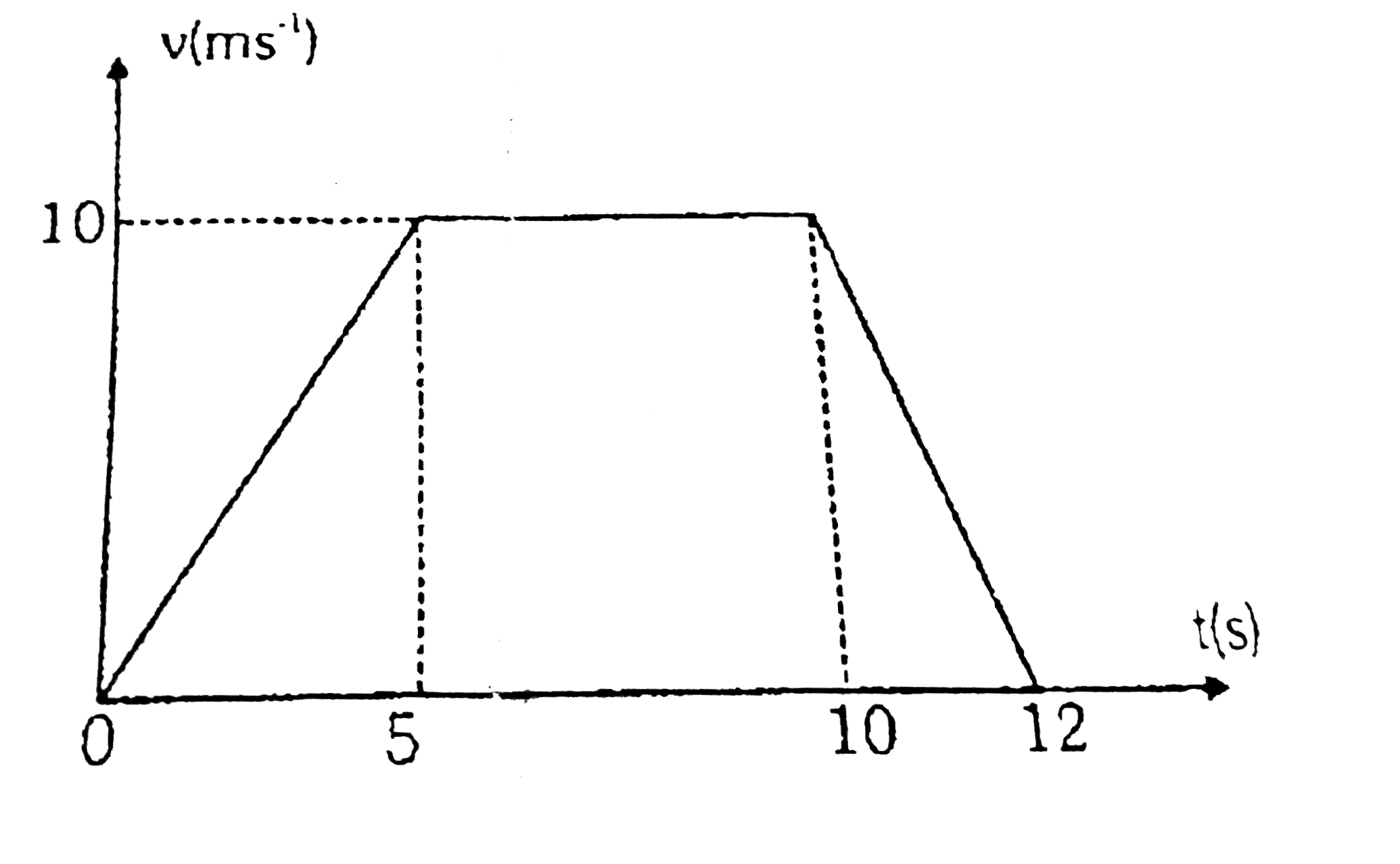
Draw displacement time and acceleration -time graph for the given velocity-time graph
View SolutionDerive an expression for instantaneous velocity and acceleration of a particle executing simple harmonic motion.
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View Solution