The upper portion of an inclined plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comesto rest at the foot.If the ratio ofthe smooth length to rough length is w : find the coefficient of friction.
The correct Answer is:[m+nn]
To solve the problem step-by-step, we will analyze the forces acting on the particle as it slides down the inclined plane and apply the work-energy principle.
Step 1: Identify the components of the inclined plane
- The inclined plane has two sections: a smooth upper portion of length L and a rough lower portion of length L′.
- The angle of inclination is given as α.
- The ratio of the smooth length to the rough length is given as LL′=w.
Step 2: Set up the work-energy principle
- The particle starts from rest at the top and comes to rest at the bottom. Therefore, the initial kinetic energy (KE_initial) and final kinetic energy (KE_final) are both zero.
- According to the work-energy principle, the total work done by all forces is equal to the change in kinetic energy:
Wtotal=KEfinal−KEinitial=0−0=0
Step 3: Calculate the work done by gravity
- The work done by gravity as the particle moves down the incline can be calculated using the vertical height:
Wgravity=mgh
- The vertical height h can be expressed in terms of the lengths of the inclined plane:
h=(L+L′)sinα
- Thus, the work done by gravity becomes:
Wgravity=mg(L+L′)sinα
Step 4: Calculate the work done by friction
- The frictional force acting on the particle while it moves down the rough portion is given by:
Ffriction=μmgcosα
- The work done by friction as the particle moves down the rough portion (length L′) is:
Wfriction=−Ffriction⋅L′=−μmgcosα⋅L′
Step 5: Set up the equation for total work done
- According to the work-energy principle, the total work done is zero:
Wgravity+Wfriction=0
- Substituting the expressions for work done:
mg(L+L′)sinα−μmgcosα⋅L′=0
Step 6: Simplify the equation
- Cancel mg from both sides:
(L+L′)sinα=μcosα⋅L′
- Rearranging gives:
μ=(L+L′)sinαL′cosα
Step 7: Substitute the ratio LL′=w
- From the ratio LL′=w, we can express L as L′⋅w:
L=wL′
- Substitute L into the equation:
μ=(wL′+L′)sinαL′cosα=(w+1)L′sinαL′cosα
- Simplifying further:
μ=(w+1)sinαcosα=(w+1)tanα
Final Result
The coefficient of friction μ is given by:
μ=(w+1)tanα
- The inclined plane has two sections: a smooth upper portion of length L and a rough lower portion of length L′.
- The angle of inclination is given as α.
- The ratio of the smooth length to the rough length is given as LL′=w.
- The particle starts from rest at the top and comes to rest at the bottom. Therefore, the initial kinetic energy (KE_initial) and final kinetic energy (KE_final) are both zero.
- According to the work-energy principle, the total work done by all forces is equal to the change in kinetic energy:
Wtotal=KEfinal−KEinitial=0−0=0
- The work done by gravity as the particle moves down the incline can be calculated using the vertical height:
Wgravity=mgh
- The vertical height h can be expressed in terms of the lengths of the inclined plane:
h=(L+L′)sinα
- Thus, the work done by gravity becomes:
Wgravity=mg(L+L′)sinα
- The frictional force acting on the particle while it moves down the rough portion is given by:
Ffriction=μmgcosα
- The work done by friction as the particle moves down the rough portion (length L′) is:
Wfriction=−Ffriction⋅L′=−μmgcosα⋅L′
- According to the work-energy principle, the total work done is zero:
Wgravity+Wfriction=0
- Substituting the expressions for work done:
mg(L+L′)sinα−μmgcosα⋅L′=0
- Cancel mg from both sides:
(L+L′)sinα=μcosα⋅L′
- Rearranging gives:
μ=(L+L′)sinαL′cosα
- From the ratio LL′=w, we can express L as L′⋅w:
L=wL′
- Substitute L into the equation:
μ=(wL′+L′)sinαL′cosα=(w+1)L′sinαL′cosα
- Simplifying further:
μ=(w+1)sinαcosα=(w+1)tanα
The coefficient of friction μ is given by:
μ=(w+1)tanα
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
The upper portion of an incline plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comes to rest at the fool. If the ratio of the smooth length to rough length is 2:1 and coefficient of frection is n tanα, then write the value of n.
View SolutionThe upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
View Solution
Knowledge Check
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
A(a) 2cosϕB(b) 2sinϕC(c) tanϕD(d) 2tanϕThe upper half of an inclined plane of inclination 45∘ is perfectly smooth while the lower half is rough. A block starting from rest at the top comes back to rest at the bottom. The coefficient of friction for the lower half is
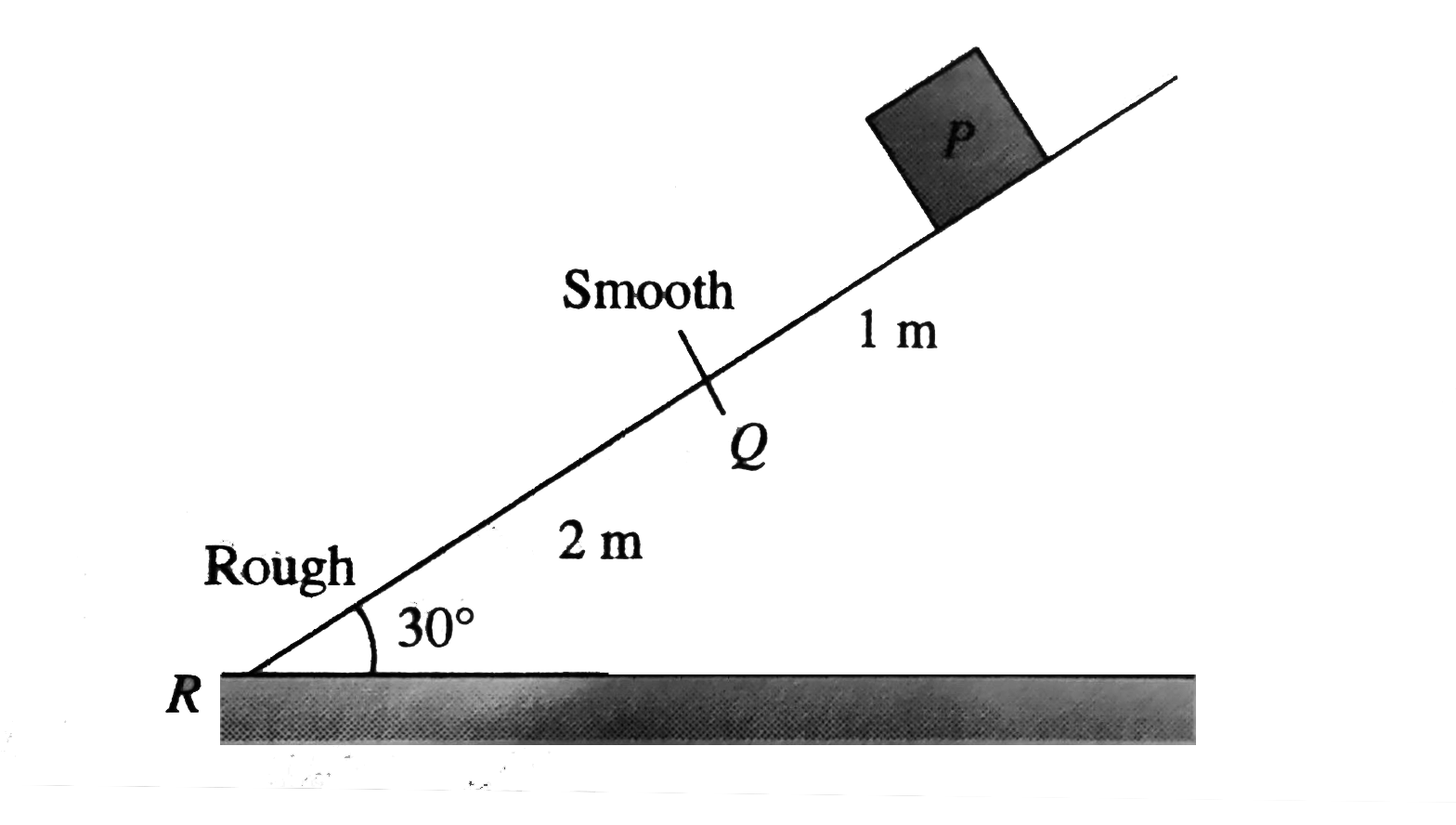
A1√2B1C√2D2A block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
 A(a) 2√3B(b) √32C(c) √34D(d) √35
A(a) 2√3B(b) √32C(c) √34D(d) √35
A body is released from rest from the top of an inclined plane of length L and angle of inclination θ ,.The top of plane of length LN (N>1) is smooth and the remaining part is rough.If the body comes to rest on reaching the bottom of the plane, then the value of coefficient of friction of rough surface is ?
View SolutionThe upper half of an inclined plane of inclination 'θ' is perfectly smooth while the lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom. The coefficient of friction between the block and the lower half of the plane is given by
View SolutionThe upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough . A block starting from rest at the top of the plane will again comes to rest at the bottom , if the coefficient of friction between the block and lower hald of the plane is given by
View SolutionThe upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
View SolutionA particle is resting on a rough inclined plane with inclination α The angle of friction is λ. The particle will be at rest if and only if
View Solution
