The v−s and v2−s graph are given for two particles. Find the accelerations of the particles at s=0.
 .
.
-8, -0.2
9, 0.2
8, 0.3
9, 0.3
The correct Answer is:A
a1=vdvds, where v=20ms−1 (at s=0)
and dvds=−25=a1v=a120
Then, a1=−8ms−2
a2=12d(v2)ds, where d(v2)ds=−25
Then, a2=−0.2ms−2.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
The velocity-time graph of a moving particle is given below. The acceleration of the particle at t = 5 s will be
View SolutionA particle moves in a circle of radius 1.0cm with a speed given by v=2t , where v is in cm/s and t in seconds.
(a) Find the radial accerleration of the particle at t=1s .
(b) Find the tangential accerleration of the particle at t=1s .
Find the magnitude of net accerleration of the particle at t=1s .
View Solution
Knowledge Check
If velocity of a particle is given by v=2t2−2 then find the acceleration of particle at t = 2 s.
A0B2C4D8If velcotiy of a particle is given by v=2t−1 then find the acceleration of particle at t = 2s.
A2B4C8D6A particle moves in a circular path such that its speed v varies with distance s as v=α√s, where α is a positive constant. Find the acceleration of the particle after traversing a distance s.
Aα√14+s2R2Bα2√14+sRCα√14+sRDα2√14+s2R2
A particle moves in circle of radius 1.0 cm at a speed given by v=2.0 t where v is in cm/s and t in seconeds. A. find the radia accelerationof the particle at t=1 s. b. Findthe tangential acceleration at t=1s. c.Find the magnitude of the aceleration at t=1s.
View SolutionA particle moves in a circular path such that its speed v varies with distance s as v=α√s where α is a positive constant. If the acceleration of the particle after traversing a distance s is [α2√x+s2R2] find x.
View SolutionReferrring to the v2−s diagram of a particle, find the displacement of the particle durticle during the last two seconds.
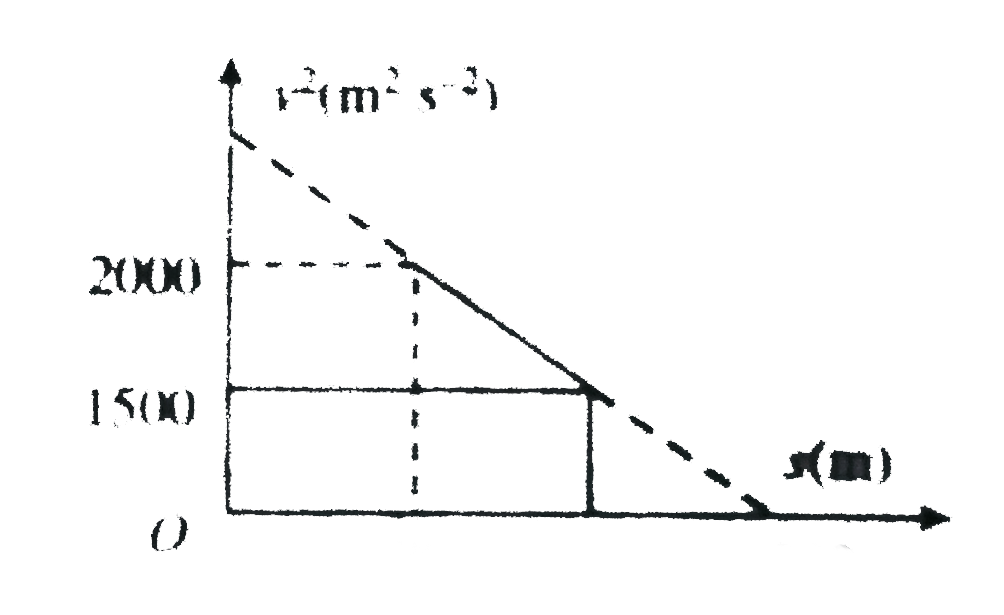 .
.
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
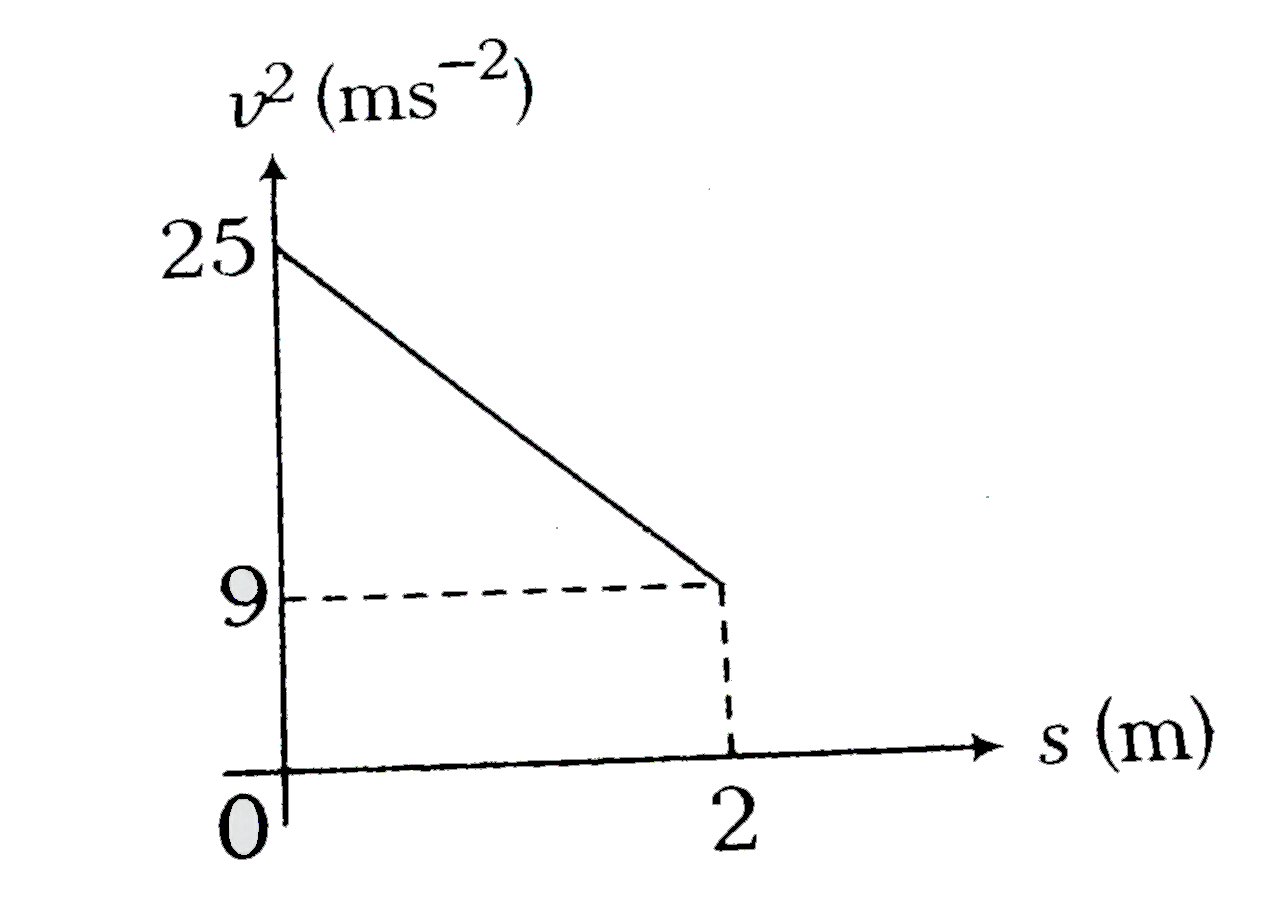
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View Solution
