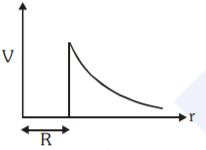
The variation of electrostatic potential with radial distance r from centre of positively charged metallic thin shell of radius R is given by graph
##N∃TRE20_PHY33_O02##
##N∃TRE20_PHY33_O03##
##N∃TRE20_PHY33_O04##
The correct Answer is:B
To solve the problem of the variation of electrostatic potential with radial distance r from the center of a positively charged metallic thin shell of radius R, we will analyze the potential in three regions: inside the shell, on the surface, and outside the shell.
1. Understanding the Electric Field Inside the Shell:
- For a metallic shell, the electric field E inside the shell (for r<R) is zero. This is due to the property of conductors in electrostatic equilibrium, where charges reside on the surface and do not create an electric field inside.
Hint: Recall that for a conductor in electrostatic equilibrium, the electric field inside is zero.
2. Potential Inside the Shell:
- Since the electric field E=0 inside the shell, the potential V remains constant throughout this region. The potential inside the shell is equal to the potential at the surface.
Hint: Remember that if E=0, then dV=−Edr implies dV=0.
3. Calculating the Potential on the Surface:
- The potential V at the surface of the shell (for r=R) can be calculated using the formula for the potential due to a point charge:
V(R)=14πϵ0⋅QR
- Here, Q is the total charge on the shell.
Hint: Use the formula for the potential due to a point charge to find the potential at the surface.
4. Potential Outside the Shell:
- For r>R, the shell behaves like a point charge located at its center. The potential at a distance r from the center is given by:
V(r)=14πϵ0⋅Qr
- This shows that the potential decreases as r increases.
Hint: Remember that outside a charged shell, the potential behaves like that of a point charge.
5. Summary of Potential Variation:
- For r<R: The potential V is constant and equal to V(R).
- For r=R: The potential is V(R)=14πϵ0⋅QR.
- For r>R: The potential V decreases as 1r.
Final Answer:
The variation of electrostatic potential V with radial distance r from the center of the positively charged metallic thin shell is:
- Constant for r<R,
- Equal to 14πϵ0⋅QR at r=R,
- Decreasing as 1r for r>R.
- For a metallic shell, the electric field E inside the shell (for r<R) is zero. This is due to the property of conductors in electrostatic equilibrium, where charges reside on the surface and do not create an electric field inside.
- Since the electric field E=0 inside the shell, the potential V remains constant throughout this region. The potential inside the shell is equal to the potential at the surface.
- The potential V at the surface of the shell (for r=R) can be calculated using the formula for the potential due to a point charge:
V(R)=14πϵ0⋅QR
- Here, Q is the total charge on the shell.
- For r>R, the shell behaves like a point charge located at its center. The potential at a distance r from the center is given by:
V(r)=14πϵ0⋅Qr
- This shows that the potential decreases as r increases.
- For r<R: The potential V is constant and equal to V(R).
- For r=R: The potential is V(R)=14πϵ0⋅QR.
- For r>R: The potential V decreases as 1r.
The variation of electrostatic potential V with radial distance r from the center of the positively charged metallic thin shell is:
- Constant for r<R,
- Equal to 14πϵ0⋅QR at r=R,
- Decreasing as 1r for r>R.
Topper's Solved these Questions
Similar Questions
The electrostatic field due to a point charge depends on the distance r as (l/r2). Similarly, indicates how each of the following quantities depends on r : (a) Intensity of light from a point source (b) Electrostatic potential due to a point source (c) Electrostatic potential due to a distance r from the center of a charged metallic sphere of radius R (r<R).
View SolutionTwo concentric spherical shells of radii r and R(r<R) have surface charge densities −σ and +σ respectively. The variation ofelectric potential V with distance x from the centre O of the shells plotted. Which of the following graphs best depict the variation qualitatively?
View Solution
Knowledge Check
The variation of electrostatic potential with radial distance r from centre of positively charged metallic thin shell of radius R is given by graph
A B
B C
C D
D
Which graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?
A
 B
B C
C D
D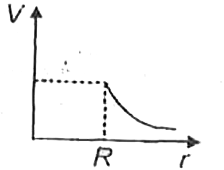
The dependence of electric potential V on the distance 'r' from the centre of a charged spherical shell is shown by :
A B
B C
C D
D
The given graph shows variation (with distance r from centre) of:

View SolutionThe given graph shows variation (with distance r from centre) of:
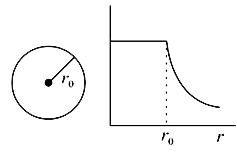
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View Solution
