The velocity of water current in a river changes with distance along the perpendicular to the river according to the law u=2u0dy for 0≤y≤d2 where u0= velocity in the mid-stream d= width of the river =2u0d(d−y) for d2≤y≤d.
A boat travels from a point O on one block of the river to the opposite bank and its steering angle is constantly changed to keep its relative velocity perpendicular to the river current. Calculate the time in which the boat will reach the other bank. The velocity of the boat in still water is u0.
The correct Answer is:πd2u0
Topper's Solved these Questions
- COMPOSITION AND RESOLUTION OF VELOCITIESBOOK - NN GHOSHCHAPTER - COMPOSITION AND RESOLUTION OF VELOCITIESEXERCISE - Exercise
25 Videos
- CENTRIPITAL AND CENTRIFUGAL FORCESBOOK - NN GHOSHCHAPTER - CENTRIPITAL AND CENTRIFUGAL FORCESEXERCISE - Exercises (B)
36 Videos
- CONDUCTION OF HEAT AND RADIATIONBOOK - NN GHOSHCHAPTER - CONDUCTION OF HEAT AND RADIATIONEXERCISE - All Questions
24 Videos
Similar Questions
A boat makes one round trip along the line AB in the river of width d. If speed of boat in still water is u and speed of water flow in the river is v, then time taken to complete the trip, is B V A
View Solution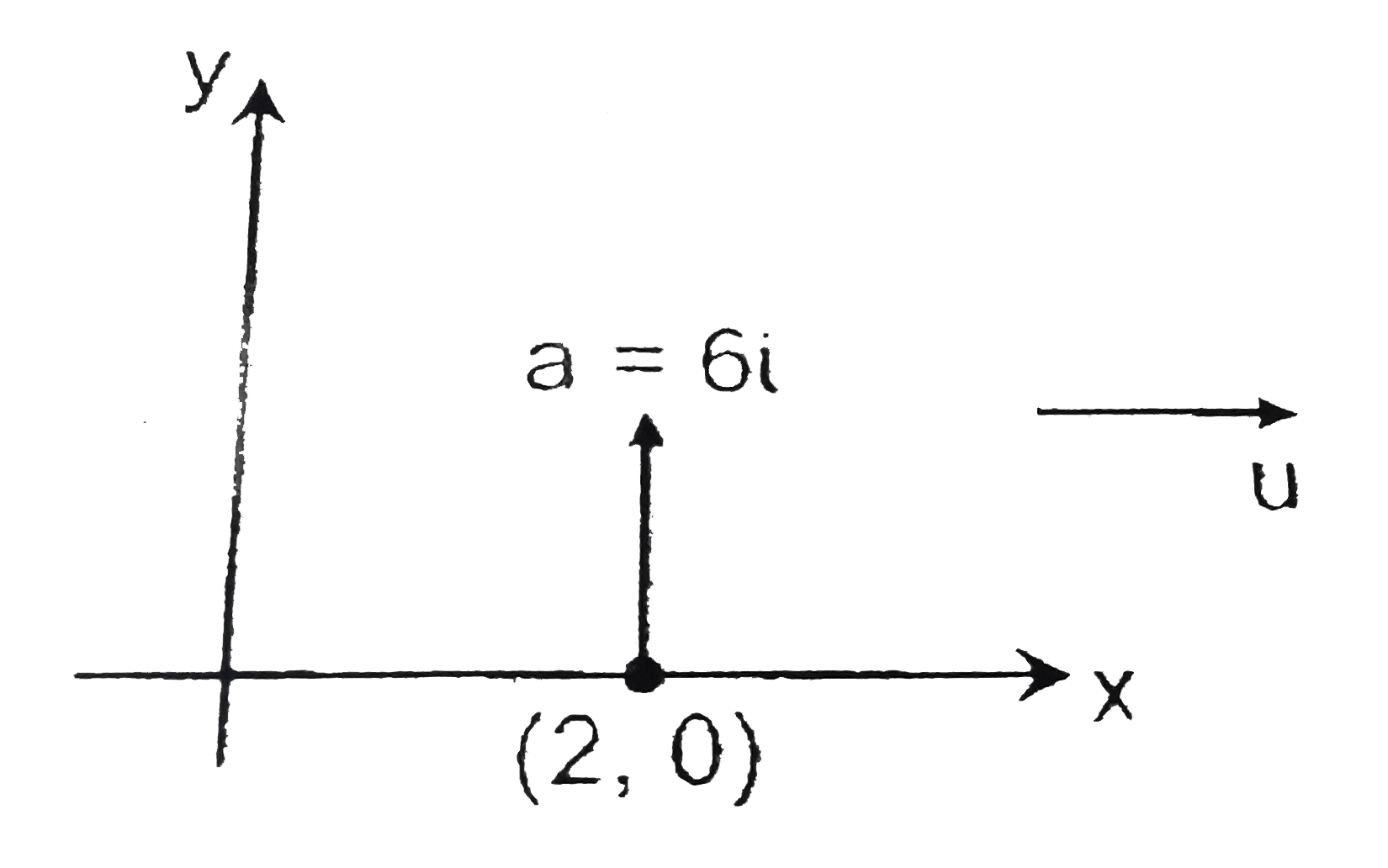
A boat starting from rest aims perpendicular to the river with an acceleration of a=6t
(where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.
View Solution
Knowledge Check
A man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
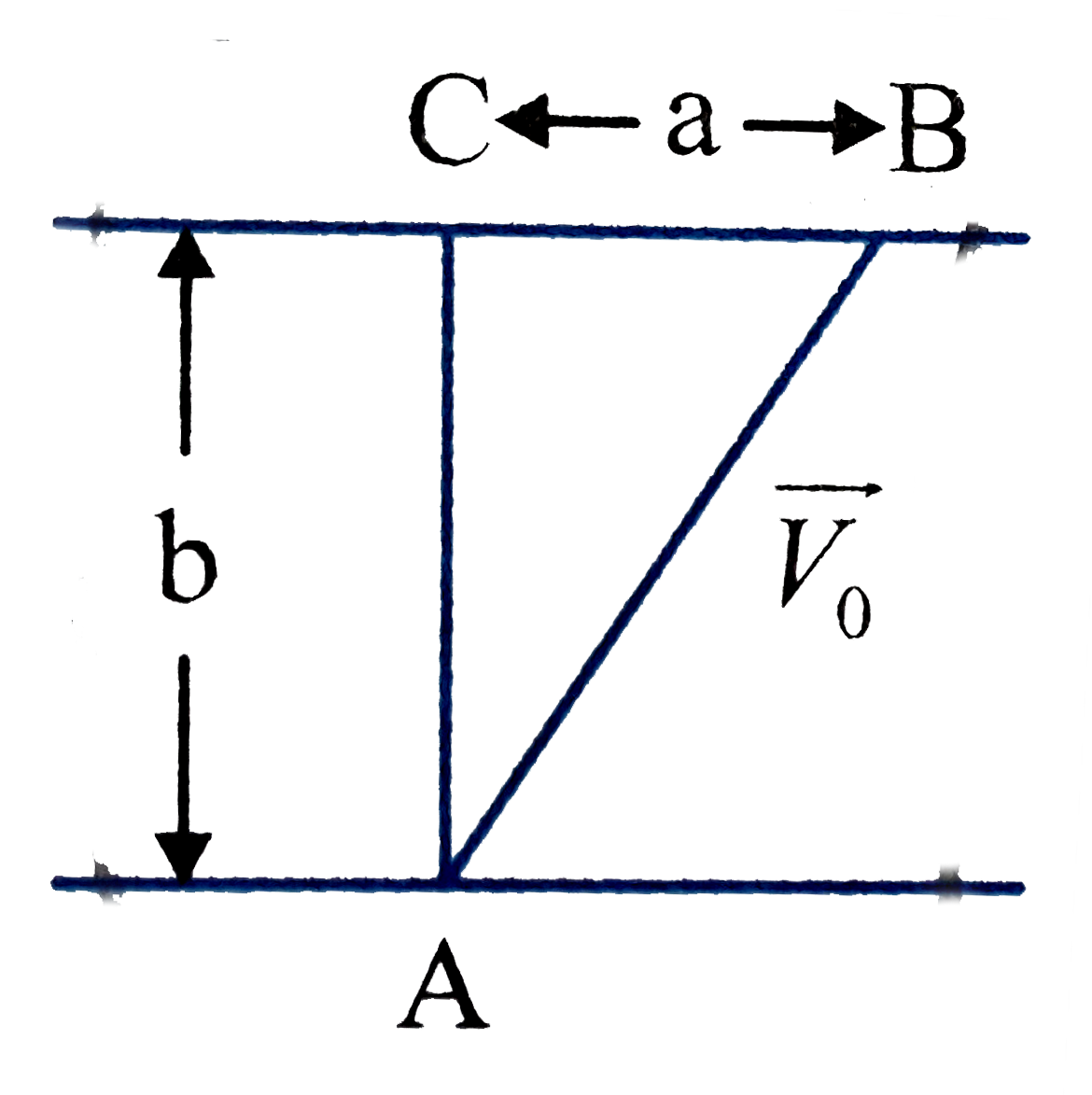 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA man can swim with a certain speed, in still water to cross a river to a point directly opposite to the starting point in time t0. When the river flows, he crosses the river directly along the same path in a time t1, If 'd' be the river width, Then the velocity of water current is:
Ad√t1t0Bdt1t0√t21−t20Cd√t21−t20Dd√(t21+t20)t1t0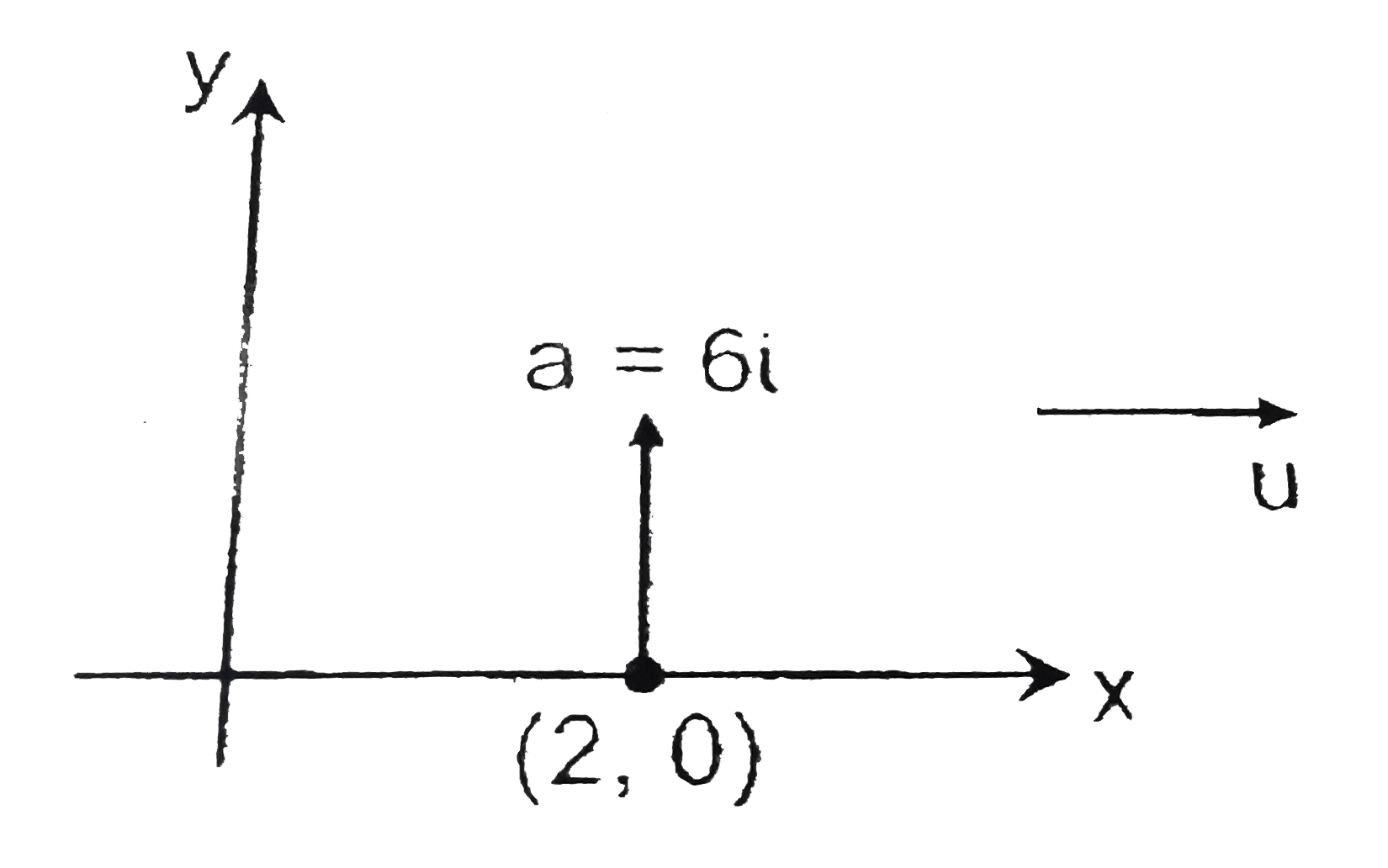
A boat starting from rest aims perpendicular to the river with an acceleration of a=6t
(where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.A(x−2)=uy23Bx−2=uy13Cx−2=uy13yDx−2=u23y
The speed of river current close to banks is nearly zero. The current speed increases linearly from the banks to become maximum (=V0) in the middle of the river. A boat has speed ‘u’ in still water. It starts from one bank and crosses the river. Its velocity relative to water is always kept perpendicular to the current. Find the distance through which the boat will get carried away by the current (along the direction of flow) while it crosses the river. Width of the river is l.
View SolutionVelocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is

View SolutionA man can swim with speed u with respect to river. The widith of river is d. The speed of the river is zero at the banks and increses linearly to V0 till mid stream of the river then decreases to zero to the other bank. When man crosses the river in shoetest time, drift is equal to: (givenu>v0)
View SolutionVelocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is

View SolutionA man can swim with speed u with respect to river. The widith of river is d. The speed of the river is zero at the banks and increses linearly to V0 till mid stream of the river then decreases to zero to the other bank. When man crosses the river in shoetest time, drift is equal to: (givenu>v0)
View Solution
