Velocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is

y=x33v30
y=x22v20
y=xv0
y=√xv0
The correct Answer is:A
dvYdt=2t
∴vy=t2ordydt=t2
or y=t33
and x=v0t⇒t=xv
Substituting in Eq. (i) we have,
y=x33v30
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
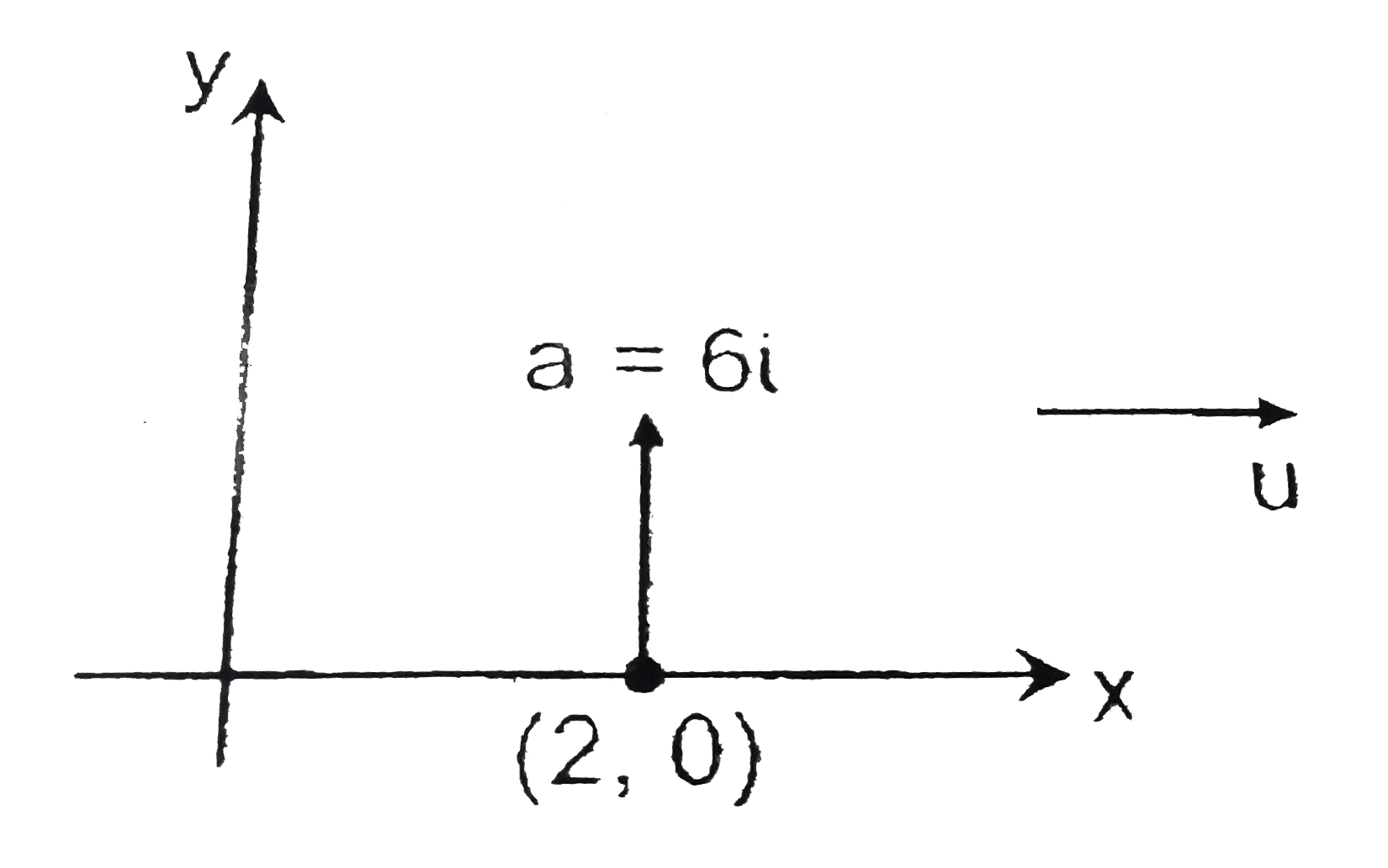
A boat starting from rest aims perpendicular to the river with an acceleration of a=6t
(where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
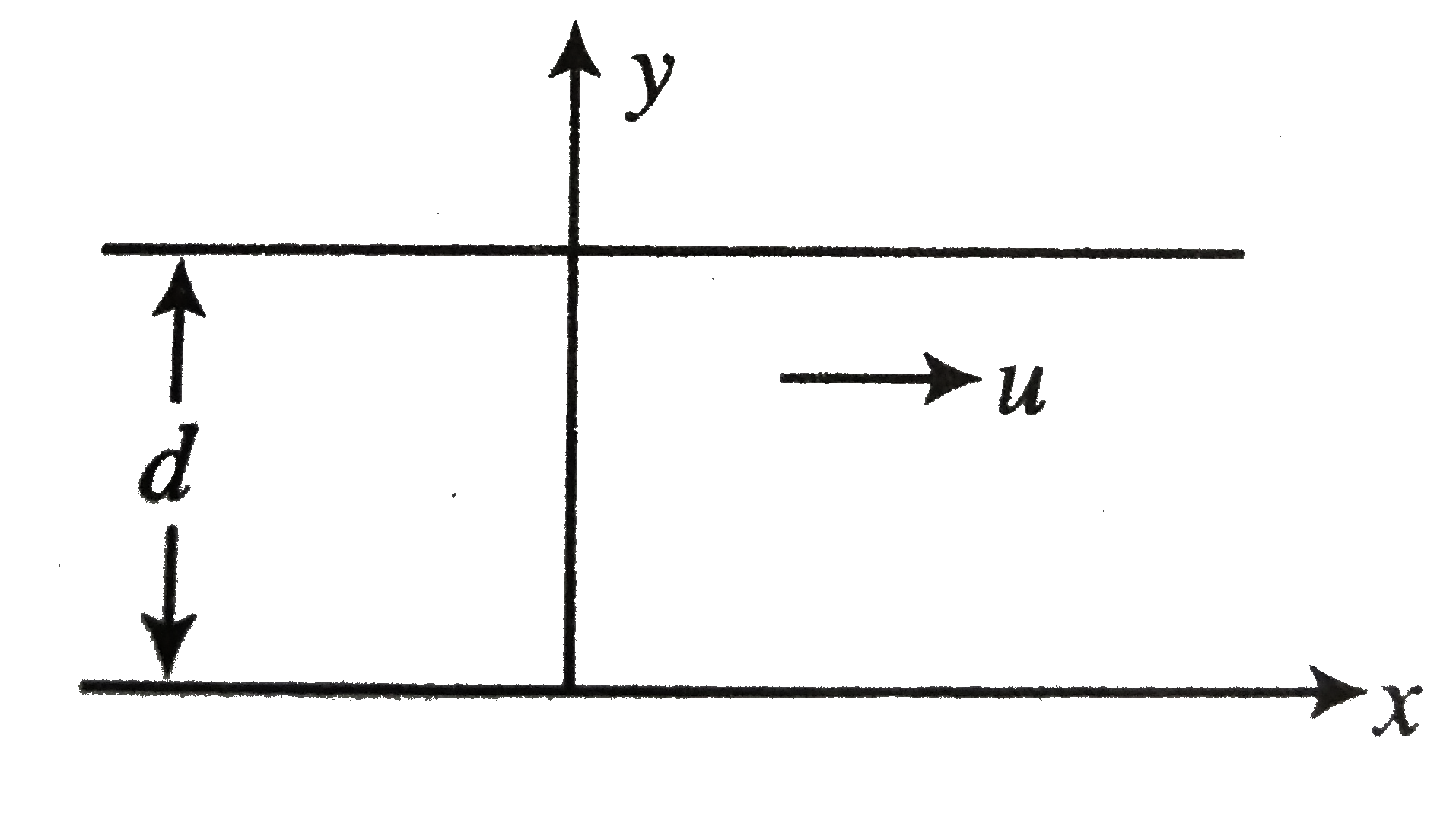
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionA swimmer can swim in still water at a rate 4.0 km/h. If he swims in a river flowing at 3.0 km/h and keeps his direction (with respect to water) perpendicular to the current, find his velocity with respect to the ground.
View SolutionIf the relation between acceleration and time for an object is given by
a=2t+4t2
Calculate the position of object from the origin at t = 4 s. Assume the object to be at rest at t=0.View SolutionA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t=14s is
 View Solution
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View Solution

