The voltage across a lamp, is 6.32V when the current passing through it is 3.4 A. Find the power consumed to appropriate significant figures.
To solve the problem, we need to calculate the power consumed by the lamp using the formula:
P=V×I
where:
- P is the power,
- V is the voltage,
- I is the current.
Step 1: Identify the given values
- Voltage V=6.32V
- Current I=3.4A
Step 2: Calculate the power
Using the formula for power:
P=6.32V×3.4A
Now, perform the multiplication:
P=6.32×3.4=21.488W
Step 3: Determine significant figures
Next, we need to consider the significant figures in our result. The voltage (6.32 V) has 3 significant figures, and the current (3.4 A) has 2 significant figures. The final result should have the same number of significant figures as the measurement with the least significant figures.
Since the current has the least significant figures (2), the power should also be reported with 2 significant figures.
Step 4: Round the result to the appropriate significant figures
The calculated power is 21.488 W, which has 5 significant figures. We need to round this to 2 significant figures:
1. The first two significant figures are 21.
2. The next digit is 4, which means we do not round up.
3. Therefore, we write it as 21.
Now, since the last digit is 5, we need to check the preceding digit to determine if we round it up or keep it the same. Since 21 is even, we round it to:
P≈22W
Final Answer
Thus, the power consumed by the lamp is:
22W
- P is the power,
- V is the voltage,
- I is the current.
- Voltage V=6.32V
- Current I=3.4A
Using the formula for power:
Next, we need to consider the significant figures in our result. The voltage (6.32 V) has 3 significant figures, and the current (3.4 A) has 2 significant figures. The final result should have the same number of significant figures as the measurement with the least significant figures.
The calculated power is 21.488 W, which has 5 significant figures. We need to round this to 2 significant figures:
2. The next digit is 4, which means we do not round up.
3. Therefore, we write it as 21.
Thus, the power consumed by the lamp is:
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.1
25 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.2
10 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
Similar Questions
The voltage across a lamp is 6.82 V when the current passing through it is 4.1 A. Find the power consumed to appropriate significant figures.
View SolutionThe voltage across a lamp is (6.0±0.1)V and the current passing through it is (4.0±0.2) ampare. Find the power consumed by the lamp.
View Solution
Knowledge Check
If a capacitor of 8μF is connected to a 220 V, 100 Hz ac source and the current passing through it is 65 mA, then the rms voltage across it is
A129.4VB12.94VC1.294VD15 V
In the figure given below, the current passing through 6Ω resistor is
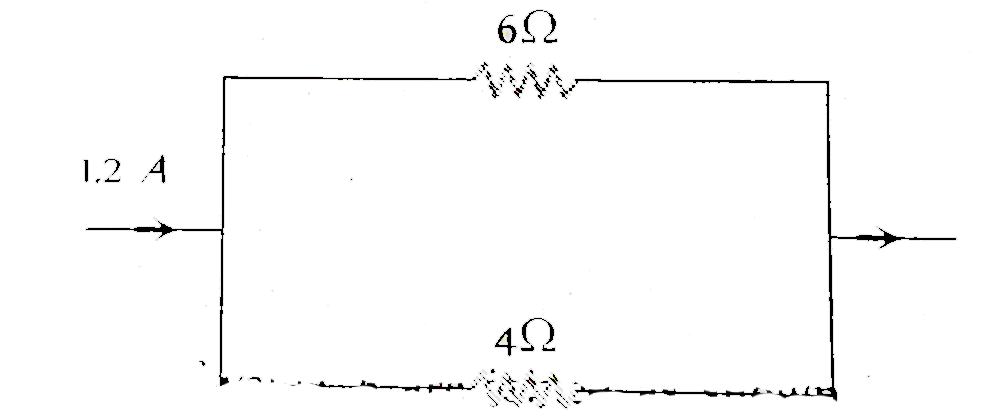
View SolutionWhen a potential difference is applied across, the current passing through
View SolutionA coil is series with a 20μF capacitor across a 230V,50Hz supply. The current taken by the circuit is 8A and the power consumed is 200W. Calculate the inductance of the coil if the current in the circuit is
(a) leading
(b) lagging
View SolutionPower P is to be delivered to a device via transmission cables having resistance Rc. If V is the voltage across R and I the current through it , find the power wasted and how can it be reduced.
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionIf an ac source is connected across ideal capacitor and current passing through it is denoted by curve (a) then instantaneous power is denoted by curve

View Solution
