The current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
3sint+3cost
3cost+3sint
3sint+3tcost
3tcost+sint
The correct Answer is:C
To find the voltage across the inductor when the current is given by i=3tsint, we will use the formula for the voltage across an inductor, which is given by:
VL=LdIdt
where L is the inductance and dIdt is the rate of change of current with respect to time.
Step 1: Identify the given values
- Inductance L=1H
- Current i(t)=3tsint
Step 2: Differentiate the current with respect to time
We need to find dIdt. Using the product rule for differentiation, we differentiate i(t)=3tsint:
dIdt=ddt(3tsint)=3sint+3tcost
Step 3: Substitute dIdt into the voltage formula
Now we substitute dIdt back into the voltage formula:
VL=LdIdt=1⋅(3sint+3tcost)
Step 4: Simplify the expression
Since L=1H, we get:
VL=3sint+3tcost
Final Answer
Thus, the voltage across the inductor is:
VL=3sint+3tcost
- Inductance L=1H
- Current i(t)=3tsint
We need to find dIdt. Using the product rule for differentiation, we differentiate i(t)=3tsint:
Now we substitute dIdt back into the voltage formula:
Since L=1H, we get:
Thus, the voltage across the inductor is:
Similar Questions
The current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionIf the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
View SolutionThe current through inductor of 2H is given by I=2tcos2t. The voltage across the inductor is
View SolutionThe current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
View SolutionA capacitor of capacitance Chas initial charge Q0 and connected to an inductor L as shown. Att=0 switch S is closed. The current through the inductor when energy in the capacitor is three times the energy of inductor is

View SolutionA 100Ω resistasnce is connected in series with a 4H inductor. The voltage across the resistor is VR=(2.0V)sin(103rad/s)t:
(a) Find the expession of circuit current
(b) Find the inductive reactance
(c) derive an expression for the voltage across the inductor,
View SolutionA 100Ω resistasnce is connected in series with a 4H inductor. The voltage across the resistor is VR=(2.0V)sin(103rad/s)t:
(a) Find the expession of circuit current
(b) Find the inductive reactance
(c) derive an expression for the voltage across the inductor,
View SolutionThe current in ampere through an inductor is
i=(20t+10)
Here t is in second. The induced emf in the inductor 4V.
Total flux linked with the inductor at t= 2 is a
View SolutionThe current in ampere through an inductor is
i=(10+20t)
Here t is in second. The induced emf in the inductor 4V.
The self inductance of the indicator is, L…..H,
View SolutionAssertion If current shown in the figure is increasing, then
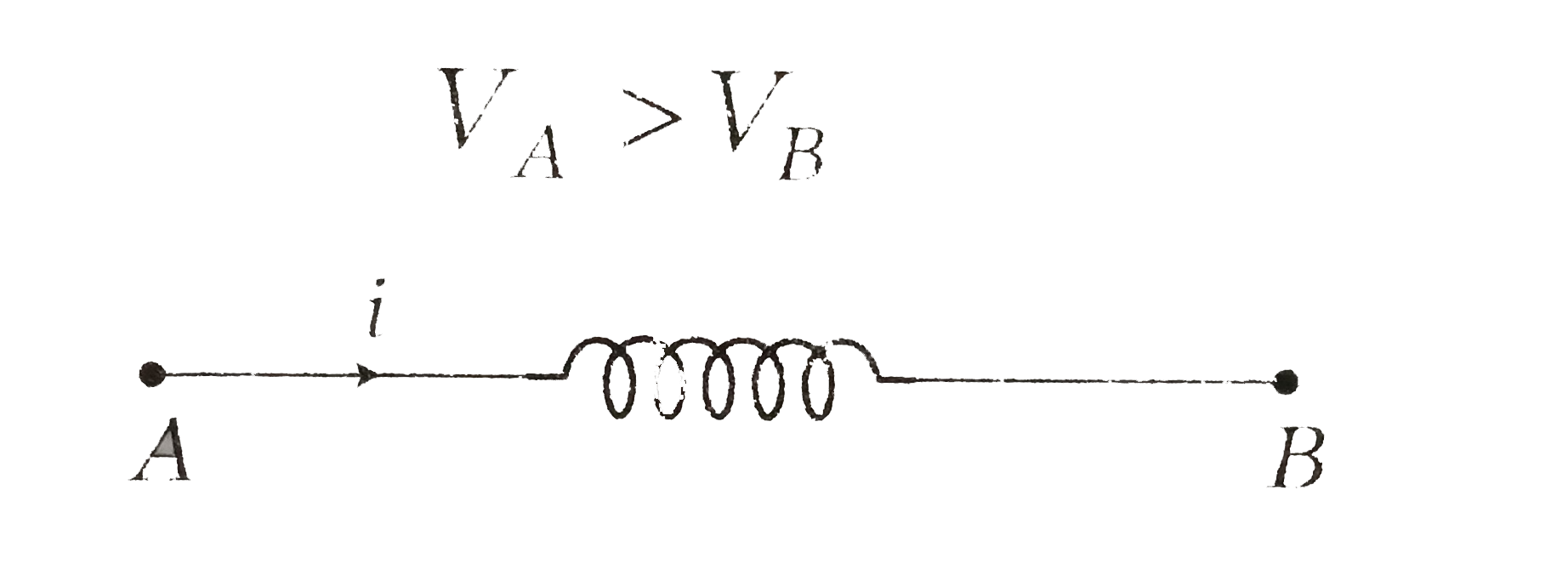
Reason IF current passing through an inductor is constant, then both ends of the inductor are at same potential.
View Solution
